Tutorial: Non-Regular Languages
2025-05-21
1 Repetition
Show \(A = \{ww: w \in \{0,1\}^*\}\) is not regular
Solution
We’ll find an infinite set \(S\) such that every pair of strings in \(S\) is distinguishable.
Let \(S = \{0^{2n}1: n \in \mathbb{N}\}\). Note that \(S\) is infinite since it contains at least one string for every natural number.
Let \(x, y \in S\) with \(x \neq y\). Then \(x = 0^{2i}1\) and \(y = 0^{2j}1\) for some \(i \neq j\). WLOG, assume \(i < j\).
Then, I claim that \(0^{2i}1\) is a distinguishing string for \(x\) and \(y\). We have
\(0^{2i}10^{2i}1 \in A\). We’ll show that \(z = 0^{2j}10^{2i}1 \notin A\). Note that \(z\) is a string of length \(2(i + j) + 2\), thus splitting \(z\) in two equal parts, we have that each of the parts have length \(i + j + 2\). Since \(i + j + 1 < 2j + 1\), we have that the first half the \(z\) consists of entirely \(0\)s. The second half contains at least 2 \(1\)s, so \(z \neq ww\) for any \(w \in \Sigma^*\) and thus \(z \not \in A\).
2 Regular?
2.1
For each of the languages below, guess whether or not the language is regular using the intuition that regular languages require a finite amount of memory. If the language is not regular, prove formally that the language is not regular using both methods we learned in class today.
\(\{w: w\text{ contains 001 as a substring}\}\)
\(\{w: w\text{ has more than one hundred 0s}\}\)
\(\{w: w\text{ has more 0s than 1s}\}\)
\(\{w: w\text{ has more 0s mod 10 than 1s mod 10}\}\)
\(\{w: w\text{ has twice as many 0s as 1s}\}\)
Solution
- Regular. Only need to store the last 2 letters read and whether or not you have already seen 001 or note
- Regular. Only need to store a counter which takes value at most 100.
- Not Regular. Need to store number of 0s which can be an arbitrarily large counter
- Regular. Only need to store two counters, each taking value at most 10.
- Not Regular. Need to store number of 0s which can be an arbitrarily large counter.
We’ll show 3 is not regular.
(MNT) By the Myhill-Nerode Theorem, it suffices to find an infinite set of strings that are pairwise distinguishable relative to \(A\).
Let \(S = \{0^{n+1}: n \in \mathbb{N}\}\) note that \(S\) is infinite since it has at least one element for every natural number.
Now we’ll show that \(S\) is pairwise distinguishable. Let \(x, y \in S\) with \(x \neq y\). Since \(x \neq y\), we have that \(x = 0^p, y = 0^q\) for some \(p, q \in \mathbb{N}\) with \(1 < p, 1 < q\), and \(p \neq q\). WLOG, suppose \(p < q\).
Then \(x1^p = 0^p1^p \notin A\), since the number of \(0\) and \(1\)s are equal, but \(y1^p = 0^q1^p \in A\), since \(p < q\). Thus, \(x\) and \(y\) are distinguishable as required. 5. is similar.
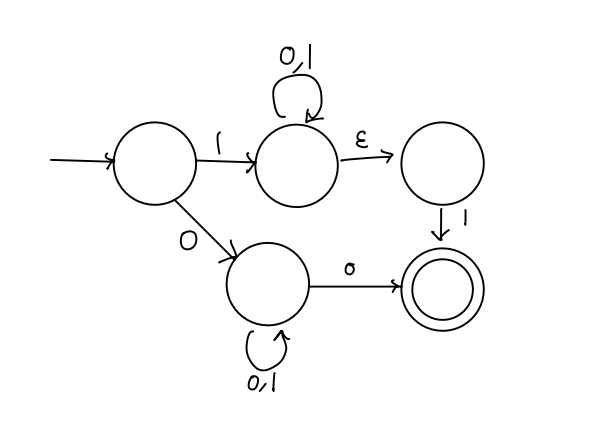
3 NFA to Regex
Convert the following NFA to a regular expression using the method from lecture.