Lecture 01: Functions
2025-05-07
Meet the people sitting next to you
- What is your favorite dessert?
- What is one thing you are excited for this summer?
Logistics
Welcome to CSC236!
Everything you need for this course can be found on the course website.
Communication
I will make all announcements through Piazza or Quercus (which will send you an email notification).
Support
- Sign up for Piazza! Please ask and answer questions!
- Come to office hours! The office hour schedule will be posted on the course calendar.
- The TAs and I are here for you, so please don’t hesitate to reach out. The best way to get in touch is through Piazza.
Course overview
Part 1: Mathematical tools.
Part 2: Algorithm correctness and runtime.
Part 3: Finite automata.
An Invitation to Theory
Questions we care about in CS Theory
Is it possible to…
- Solve problem \(X\)
- Send secure messages
- Guarantee privacy
- Send messages efficiently and robustly
- Have fair machine learning algorithms
- Maximize social welfare
- Play a game optimally
Questions we care about in CS Theory
If so, how? Also, how much…
- Time
- Space
- Processing Power
- Randomness
- Quantum bits
- …
… do we need?
The sell
For programmers:
- Rigorously analyze your programs.
- Model real-world problems as well-studied problems in theory and apply known algorithms.
In general:
- There are no compiler issues in Theory Land: problems are distilled to the core puzzle.
- CS Theory is a fascinating and new field! There are lots of unknowns, and breakthroughs happen very often.
A Motivating Problem
The question
Are there problems computers can’t solve?
Set theory review
| Subset | \(A \subseteq B\) |
| Union | \(A \cup B\) |
| Intersection | \(A \cap B\) |
| Difference | \(A \setminus B\) |
| Cardinality (size) | \(|A|\) |
Set theory review
The empty set, denoted \(\emptyset\), is the set containing nothing. I.e., \[\{\}\]
For any set, \(A\), the power set of \(A\), denoted \(\wp(A)\), is the set of all subsets of \(A\). I.e., \[\wp(A)= \{B: B \subseteq A\}\]
Functions
Functions
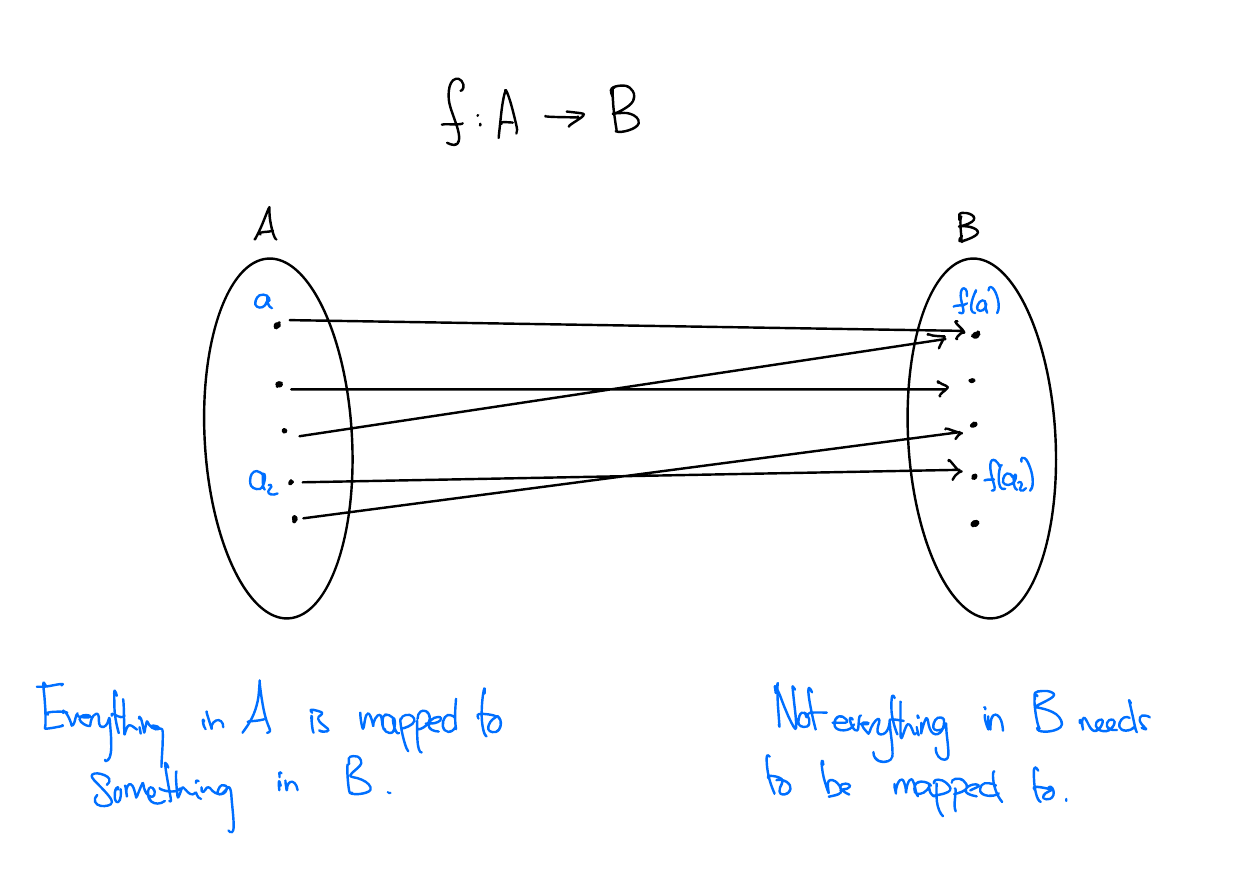
A function is a mapping from one set to another. We write a function that maps elements of \(A\) to elements of \(B\) as
\[ f: A \to B \]
\(A\) is called the domain. \(B\) is called the codomain.
Picture
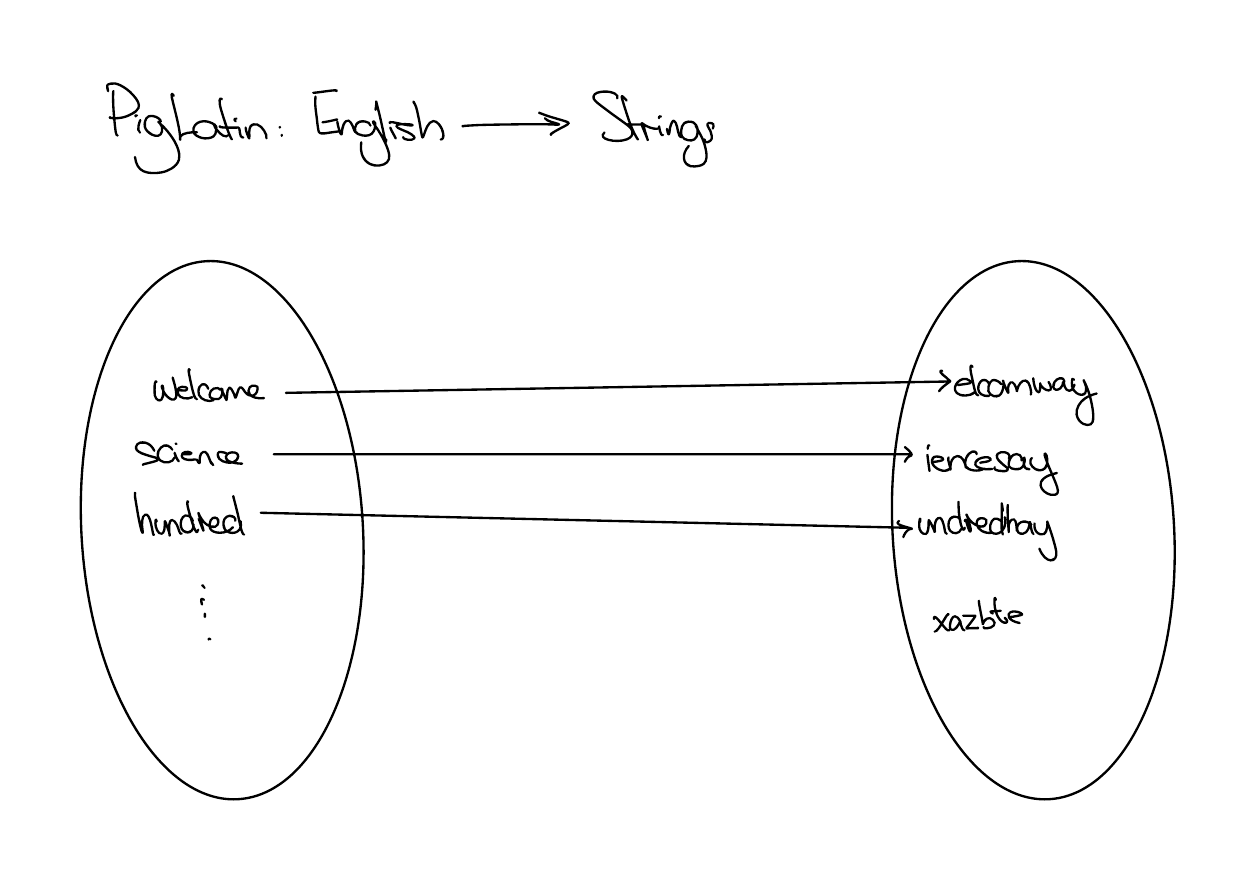
Examples
Examples
What is the domain/codomain for this function?Solution
Domain: the set of all possible lists of integers
Codomin: the set of integersIs this a function?
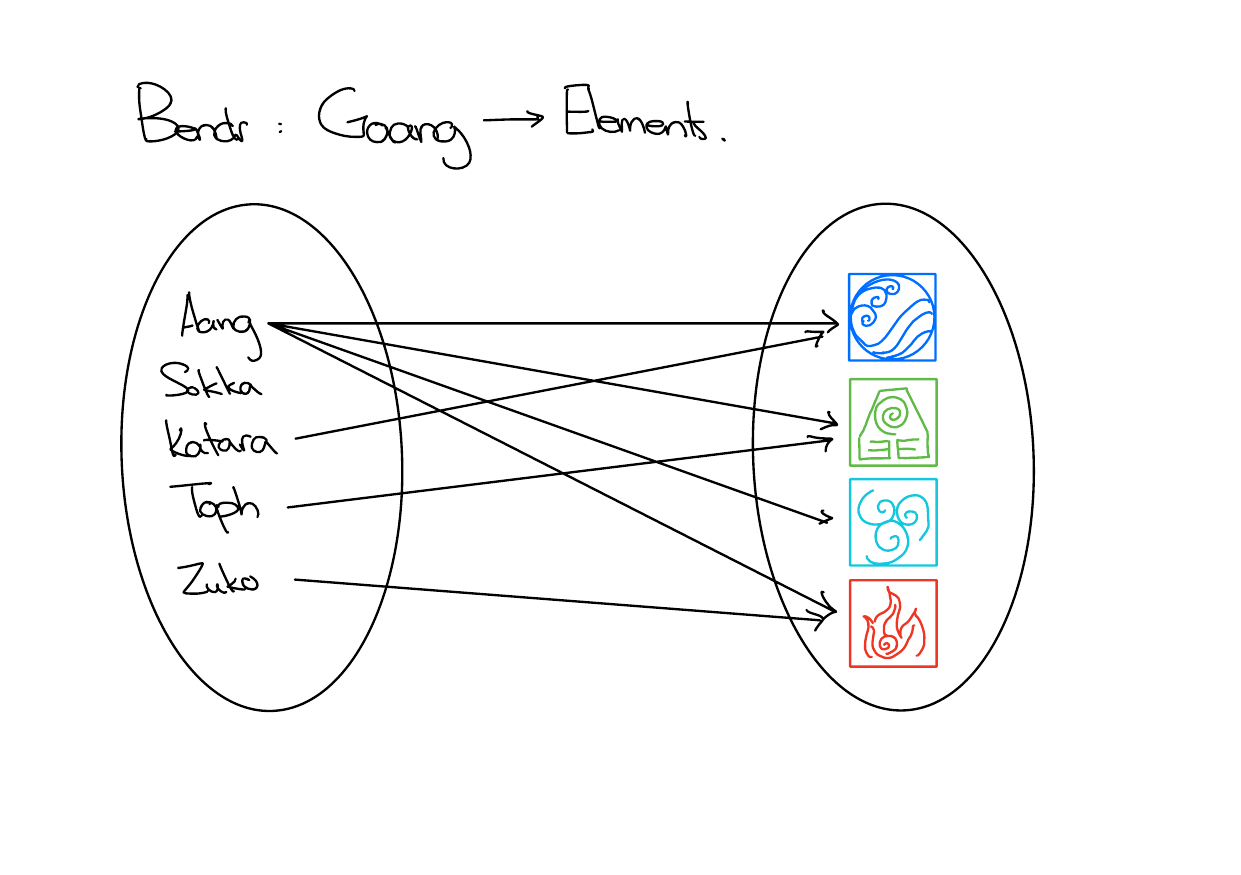
Solution
No, Aang can only be mapped to one thing, and Sokka must be mapped to something.A fix - change the codomain!
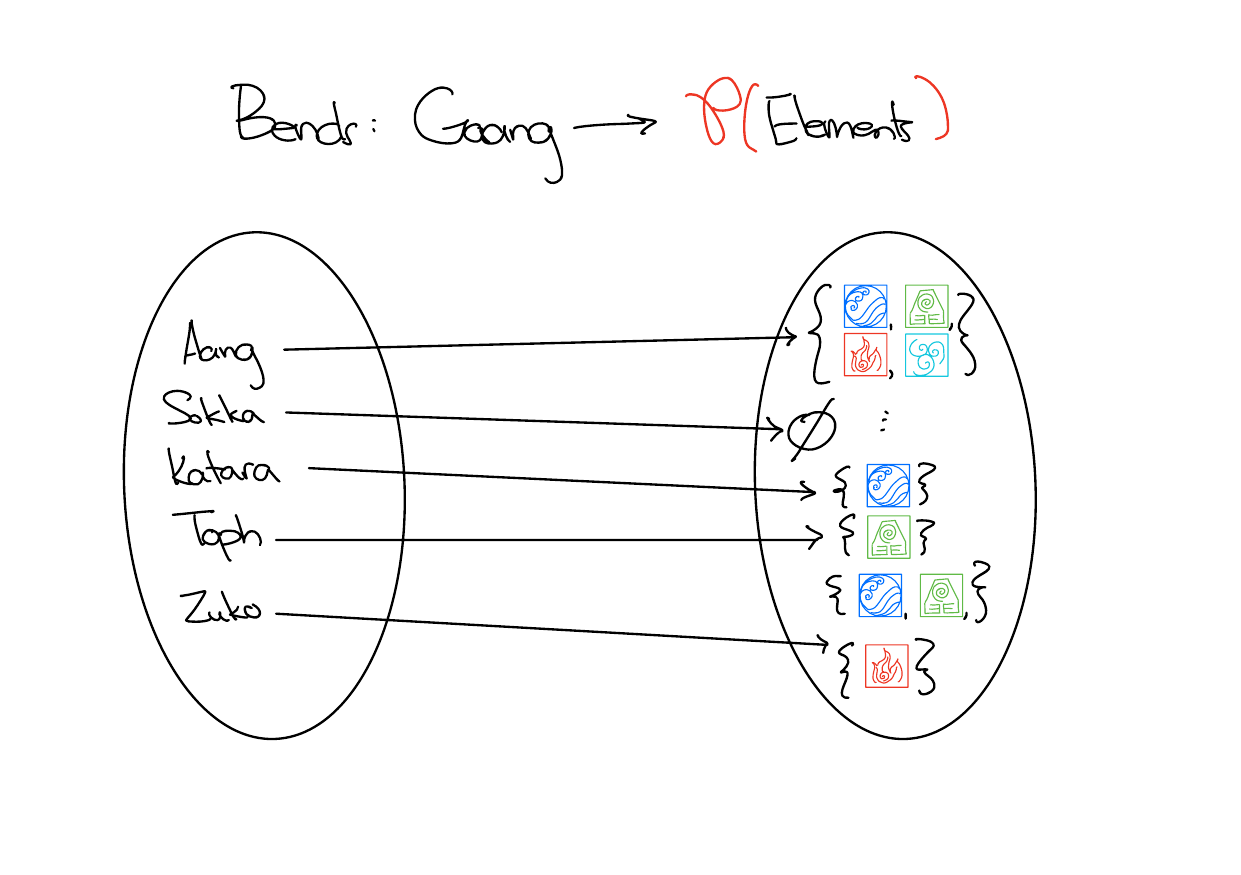
A function that we’re interested in
Properties of Functions
Injective Functions
Injective
A function is injective if nothing in the codomain is hit more than once. Formally,
Definition 1 (Injective) A function \(f:A \to B\) is injective if \[\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\]
“If the inputs are different, the outputs are different.”
Injective (contrapositive)
Sometimes, the equivalent contrapositive is easier to work with
Definition 2 A function \(f:A \to B\) is injective if \[\forall x, y \in A.(f(x) = f(y) \implies x = y)\]
“If the outputs are the same, the inputs are the same.”
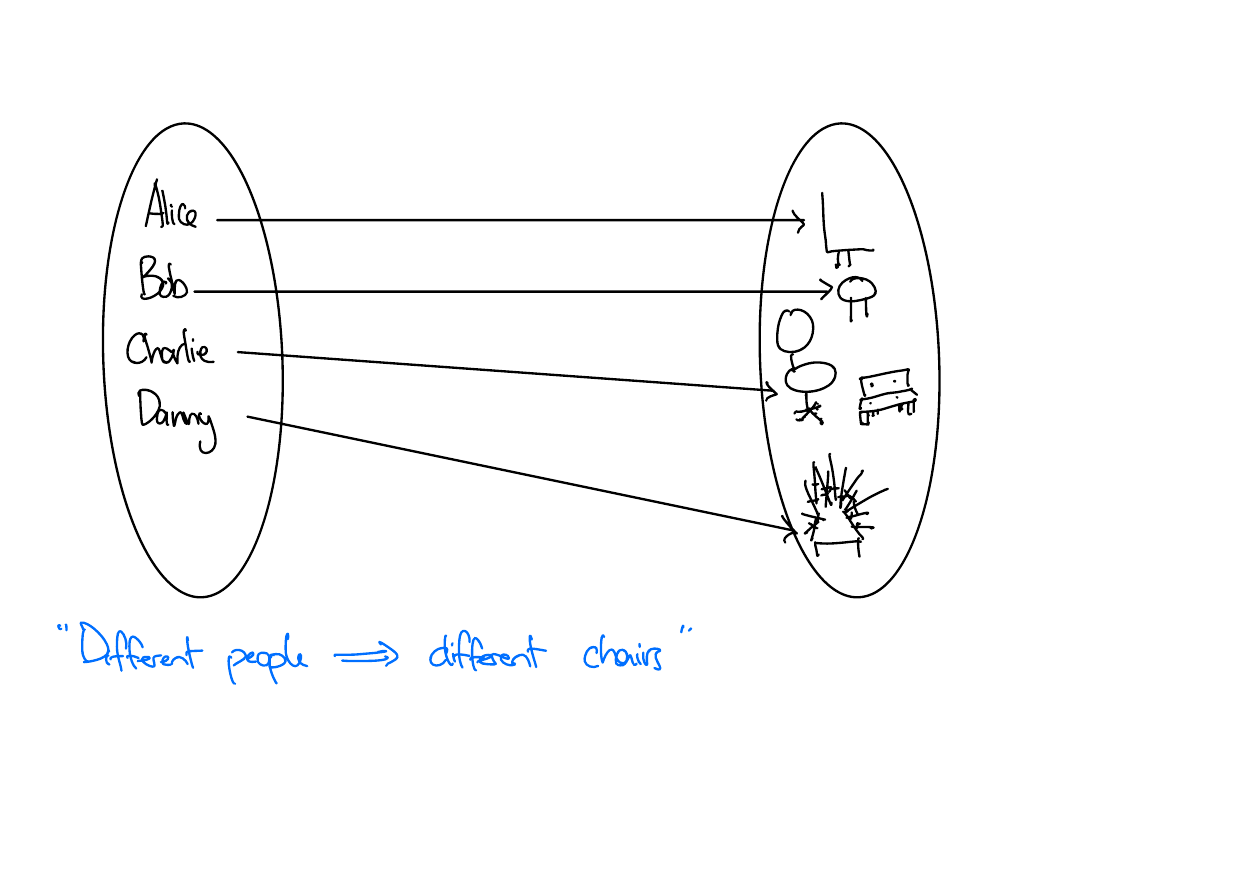
Example - People and Chairs
\(f:A \to B\) is injective if \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\)
Example - Musical Chairs
\(f:A \to B\) is injective if \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\)
Is there an injective function between these two sets?

The Pigeonhole Principle
Theorem 1 (Pigeonhole Principle) Let \(A\), \(B\) be finite sets where \(|A| > |B|\). Then there is no injective function \(f:A \to B\).
- Think of \(A\) as a set of pigeons and \(B\) as a set of pigeonholes.
- The pigeonhole principle is a fancy way of saying that if you have more pigeons than pigeonholes, no matter how you assign pigeons to pigeonholes, some pigeonhole will have at least two pigeons.
Example - Hilbert’s Hotel
\(f:A \to B\) is injective if \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\)
- An infinite hotel room with room numbers \(0, 1, 2,...\)
- A bus containing an infinite number of people shows up. Let’s call them \(a_0, a_1,a_2,...\).
- Your job is to assign customers to rooms. I.e. define an assignment function \(f:\) Customers \(\to\) Rooms
- Requirement. Only one person can stay in each room. I.e., the function is injective!
How do you do it?
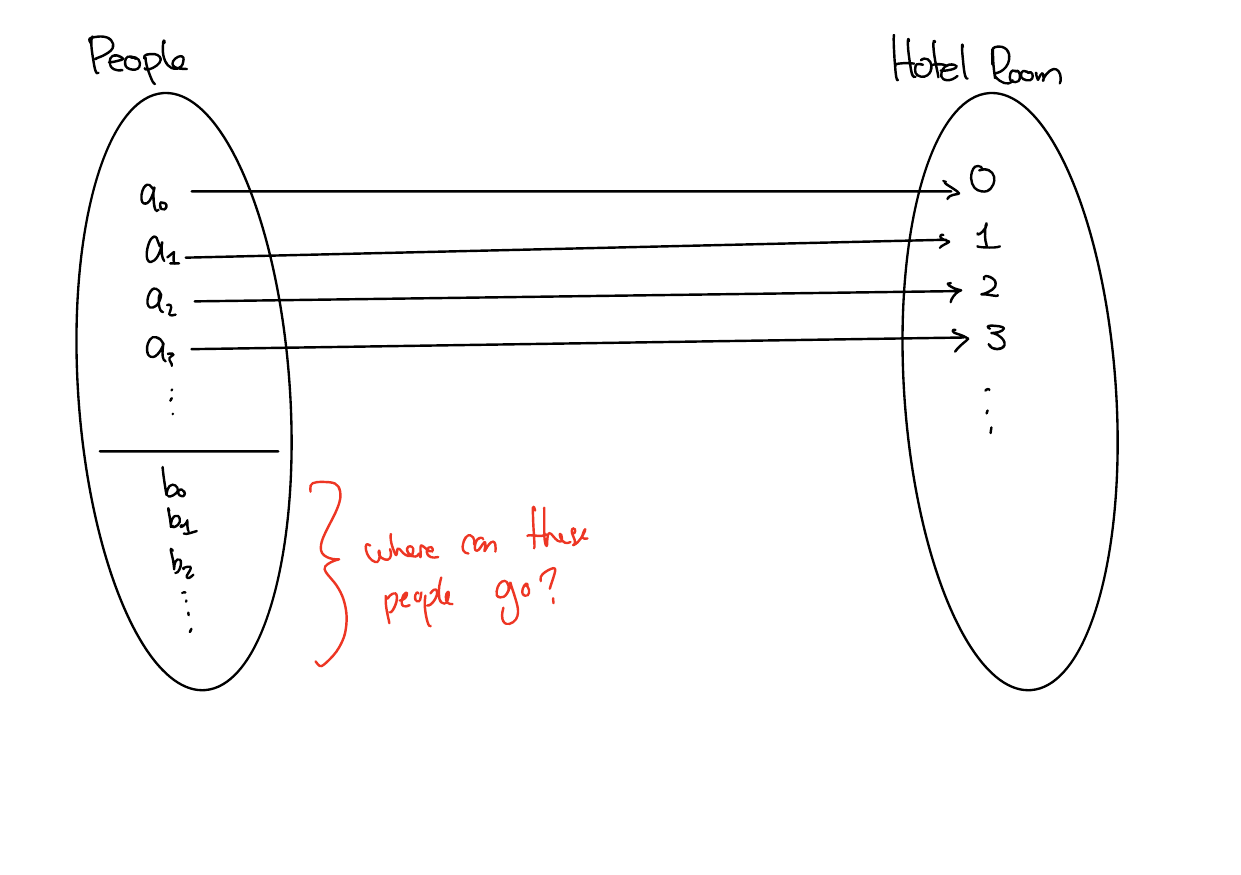
Example - Hilbert’s Hotel (level 2)
Now suppose another bus containing an infinite number of people shows up \(b_0, b_1,...\)
Currently, each room is already occupied!
However, eager to impress your boss, you try to think of a way to do the impossible - fit an infinite number of people into an already filled hotel. So, how do you do it?
Example - Hilbert’s Hotel (level 2)
Solution
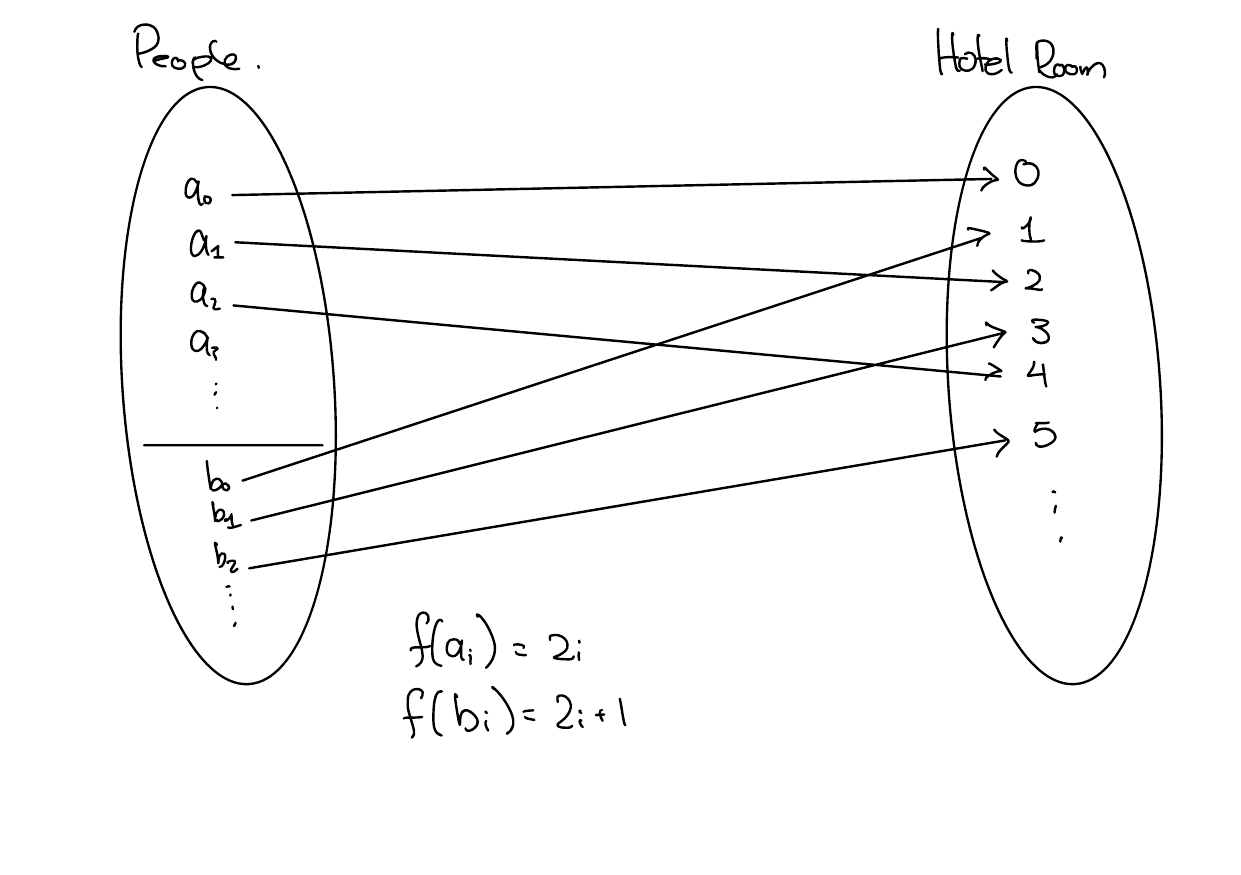
Formal Proof
\(f:A \to B\) is injective if \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\)
Proof
\[f(x) = \begin{cases} 2i & x = a_i \\ 2i + 1 & x = b_i \end{cases}\]
Let \(x, y\) be customers such that \(x \neq y\). We’ll show \(f(x) \neq f(y)\). There are several cases.
- Suppose \(x\) and \(y\) were on different buses. WLOG, assume \(x\) was on the first and \(y\) was on the second. Then \(f(x) \neq f(y)\) since \(f(x)\) is even and \(f(y)\) is odd.
- If \(x\) and \(y\) were both on the first bus, then since \(x \neq y\), \(x = a_i\) and \(y=a_j\) for some \(i \neq j\). Thus \(2i \neq 2j\) and \(f(x) \neq f(y)\) as required.
- The case where \(x\) and \(y\) were both the second bus is similar.
Hilbert’s Hotel
- Our previous example essentially shows that \(2\) time infinity is infinity.
- There are more levels to Hilbert’s Hotel to think about.
- It’s not too hard to see that if another 10 buses arrive, we can still shuffle people around so that they can all fit into the hotel.
- Can we deal with an infinite number of buses each containing an infinite number of customers?
- How about a ferry containing an infinite number of buses each containing an infinite number of customers?
Surjective Functions
A function is surjective if everything in the codomain is hit. Formally,
Definition 3 (Surjective) A function, \(f: A \to B\) is surjective if \[\forall b \in B. \exists a \in A. (f(a) = b)\]
Example
\(f\) is surjective if \(\forall b \in B. \exists a \in A. (f(a) = b)\).
Is \(f\) defined by \(f(n) = n\) surjective?
Solution
It depends on the domain/codomain! For example, \(f:\mathbb{N}\to \mathbb{N}\) defined by \(f(n) = n\) is surjective, but \(f:\mathbb{N}\to \mathbb{R}\) defined by \(f(n) = n\) is not!
It’s essential to always specify the domain and codomain when defining a function.
Bijective
A function is bijective if everything in the codomain is hit exactly once. Formally,
Definition 4 A function \(f:A \to B\) is bijective if \(f\) is both injective and surjective.
Examples
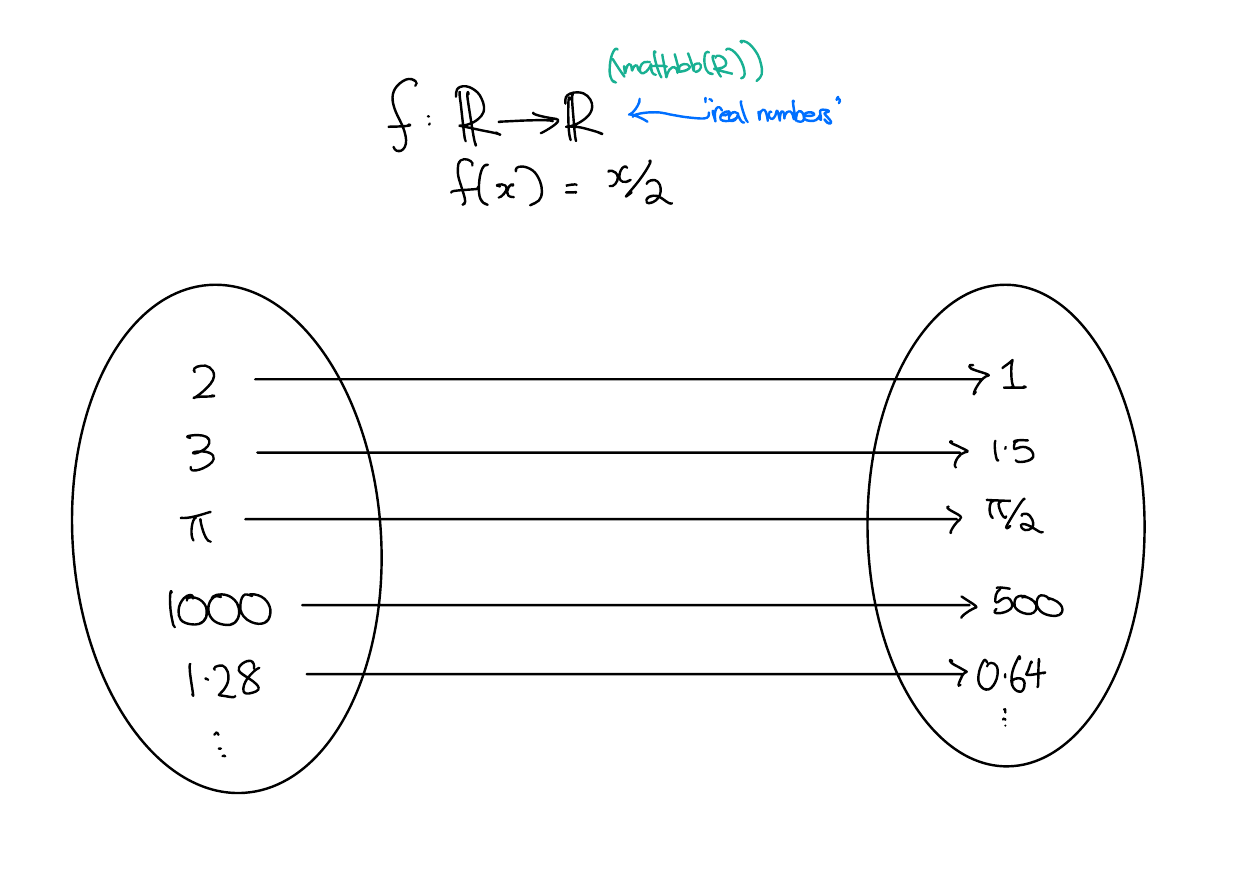
Proof - Half is Bijective
\(f\) is injective if \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\)
\(f\) is surjective if \(\forall b \in B. \exists a \in A. (f(a) = b)\).
Proof
We’ll show \(f:\mathbb{R}\to\mathbb{R}\) defined by \(f(x) = x/2\) is a bijection. To do so, we’ll show that \(f\) is both injective and surjective.
- Injective. Let \(a, b \in \mathbb{R}\) and assume \(f(a) = f(b)\). By the definition of \(f\), this implies \(a/2 = b/2\), which implies \(a = b\). Thus \(f\) is injective.
- Surjective. Let \(b \in \mathbb{R}\). To show \(f\) is surjective, we need to find some number \(a \in \mathbb{R}\) such that \(f(a) = b\). We claim that \(a = 2 b\) does the trick. We have
\[ f(a) = f(2b) = 2b/2 = b, \] and thus \(f\) is surjective.
Summary of definitions
Let \(f: A \to B\) be a function.
| \(f\) is… | if \(\forall b \in B\), \(b\) is hit… | Formally… |
|---|---|---|
| Injective | \(1\) or \(0\) times | \(\forall x, y \in A.(x \neq y \implies f(x) \neq f(y))\) |
| Surjective | at least \(1\) time | \(\forall b \in B. \exists a \in A. (f(a) = b)\) |
| Bijective | exactly \(1\) time | Injective and Surjective |
\(b \in B\) is hit \(k\) times by \(f\) if there are \(k\) distinct \(a \in A\) are such that \(f(a) = b\). I.e. \[|\{a \in A: f(a) = b\}| = k.\]
Cantor’s Theorem
Infinity
The use of \(\infty\) here is not strictly formal. More specifically, we mean \(|\mathbb{N}|\).
- Recall Hilbert’s Hotel.
- We essentially showed that \(2 \cdot \infty = \infty\).
- You’ll see either in hw or tutorial that we can fit an infinite number of buses containing an infinite number of people, i.e. \(\infty \times \infty = \infty\).
- So is there anything that Hilbert’s Hotel can’t fit?
- What is the nature of infinity?
Cantor’s Theorem
\(f\) is surjective if \(\forall b \in B. \exists a \in A. (f(a) = b)\).
Theorem 2 (Cantor’s Theorem) For any set \(A\), there is no surjection between \(A\) and \(\wp(A)\)
Relationship to Hilbert’s Hotel
Cantor’s Theorem. For any set \(A\), there is no surjection between \(A\) and \(\wp(A)\).
- Apply the theorem with \(A = \mathbb{N}\). Let \(\wp(\mathbb{N})\) be the set of customers.
- The theorem says that there is no way to map hotel rooms to customers such that every customer gets a hotel room!
I know we’ve been mapping the other way (customers to rooms), but this formulation is equivalent. Indeed, there exists a injective function from \(A \to B\) iff there is a surjective function from \(B \to A\).
Proof of Cantor’s Theorem
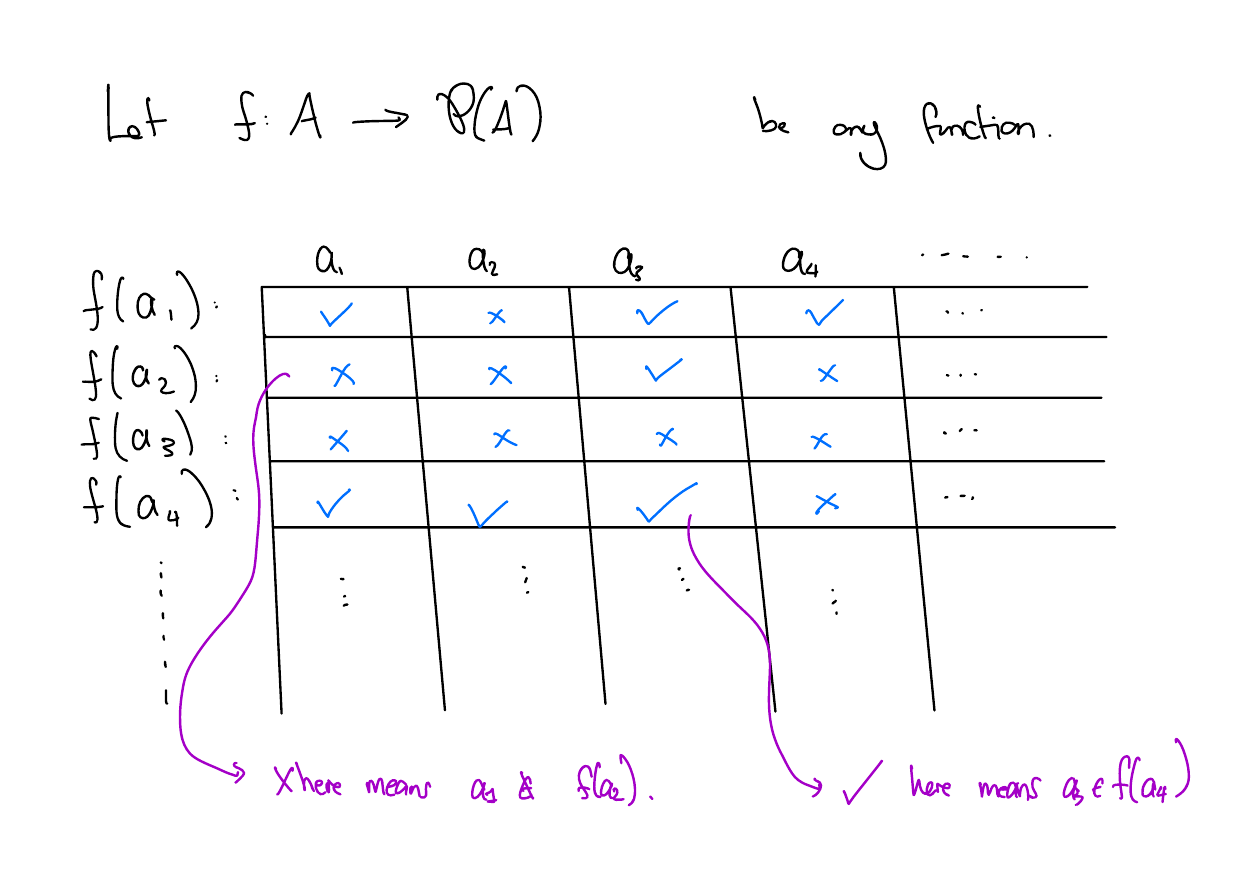
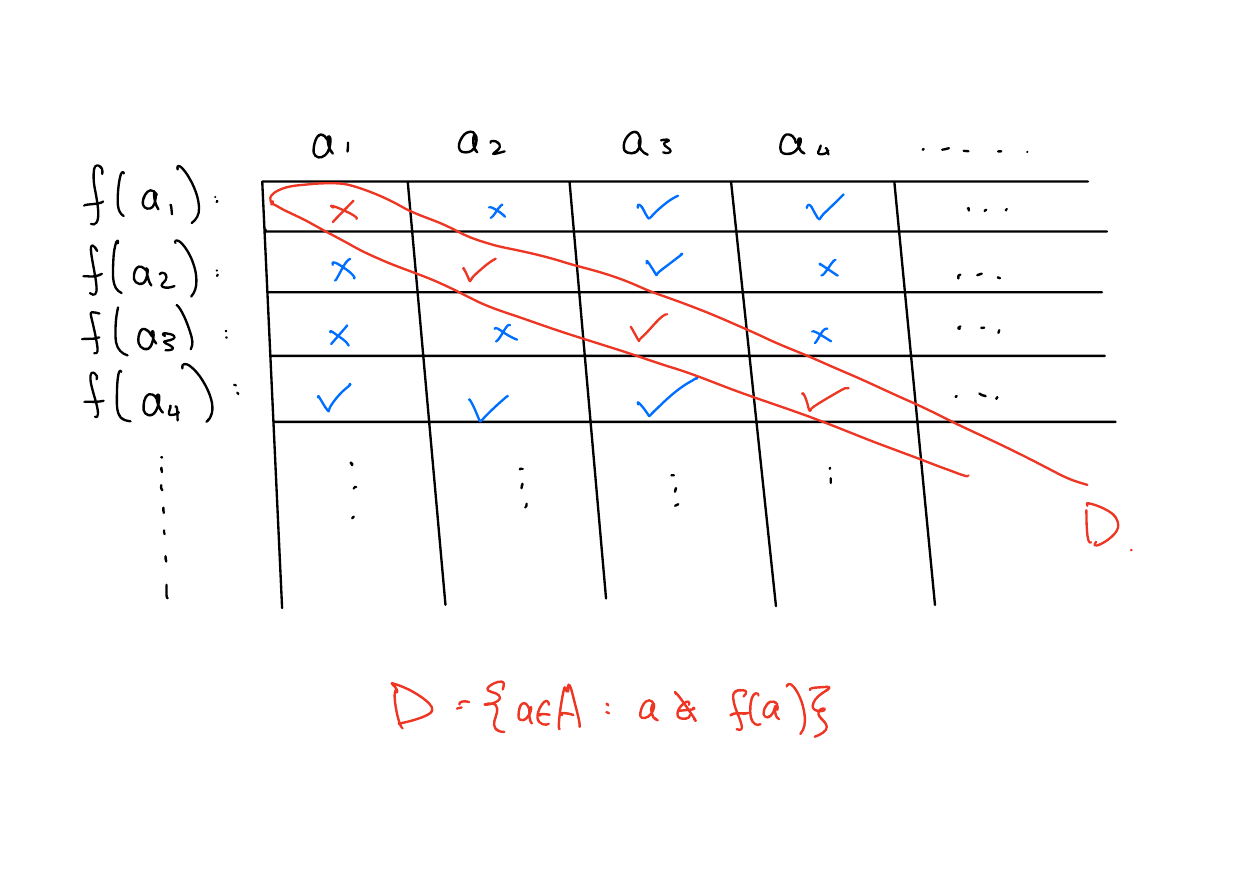
Solution
Let \(f: A \to \wp(A)\) be any function. Let \(D = \{a\in A: a \notin f(a)\}\) and note that \(D \subseteq A\), and hence \(D \in \wp(A)\).
To show \(f\) is not surjective, we’ll show that, in particular, there is no \(a \in A\) such that \(f(a) = D\).
By contradiction, assume \(D = f(a)\) for some \(a \in A\). There are two cases, either \(a \in D\) or \(a \notin D\).
- If \(a \in D\), then \(a \notin f(a)\) by the definition of \(D\). But \(f(a) = D\), so \(a \notin D\), which is a contradiction.
- Otherwise \(a \notin D\), then \(a \in f(a)\) but \(f(a) = D\) by assumption, so \(a \in D\), which is again a contradiction.
Since we reached a contradiction in both cases, our assumption must have been false. Thus, \(f\) is not surjective.
Programs and Problems
Are there problems computers can’t solve?
Let’s apply our knowledge of functions to answer the question!
Formalizing the question - Problems
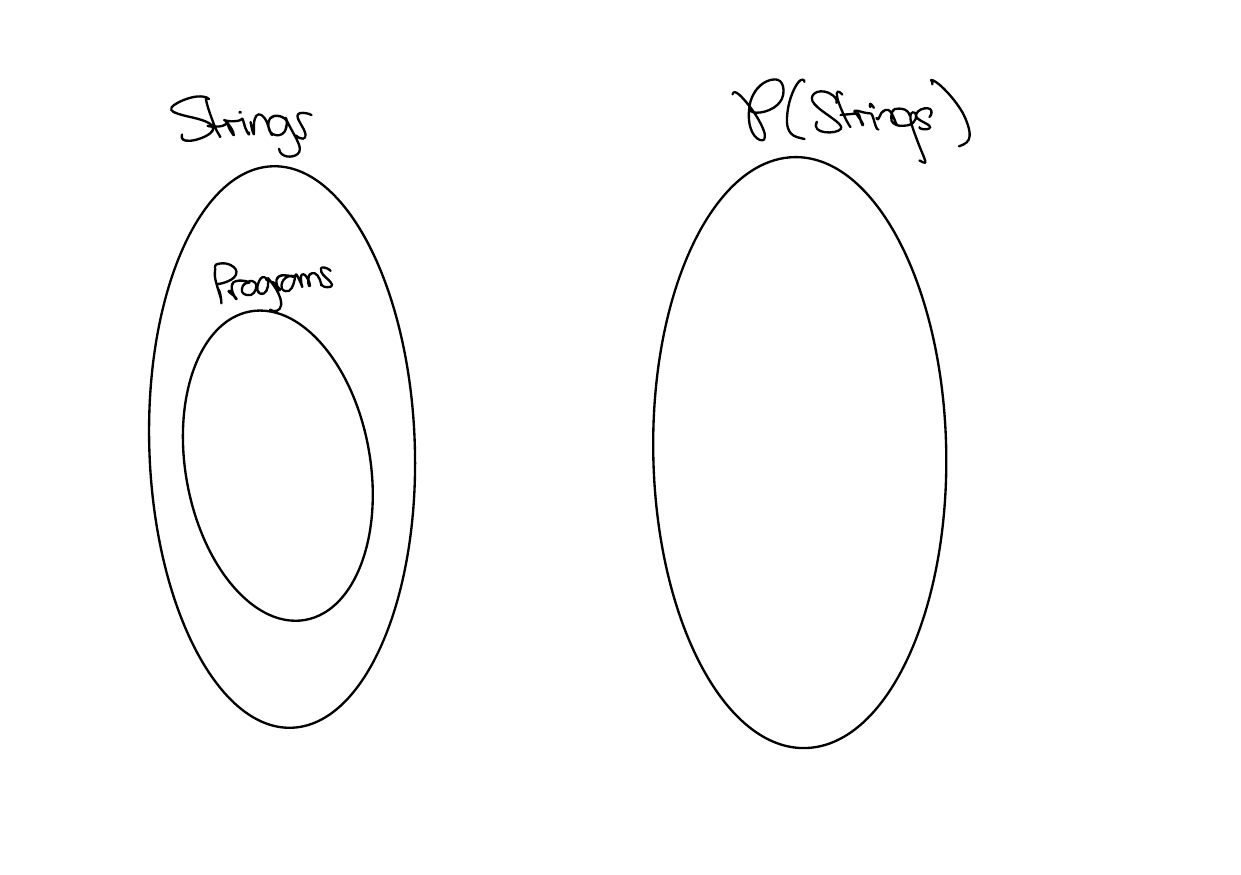
Let Strings be the set of all possible strings. For each subset \(A \subseteq\) Strings, there is the problem of determining whether or not a given input is in \(A\) or not in \(A\).
For example
\(A = \{w \in\) Strings \(: w\) is a palindrome \(\}\)
\[A = \{w: w \text{ is a C program with no syntax errors}\}.\] Let’s only consider problems of this type for now, so set
Problems \(= \wp(\)Strings \()\)
Formalizing the question - Programs
For concreteness, let’s say a program \(P\) solves a problem \(A \subseteq\) Strings, if \(\forall w \in\) Strings,
\(w \in A \iff\) \(P\) run on input \(w\) prints \(1\) and nothing else.
Identify every program with its source code (a string), so Programs \(\subseteq\) Strings
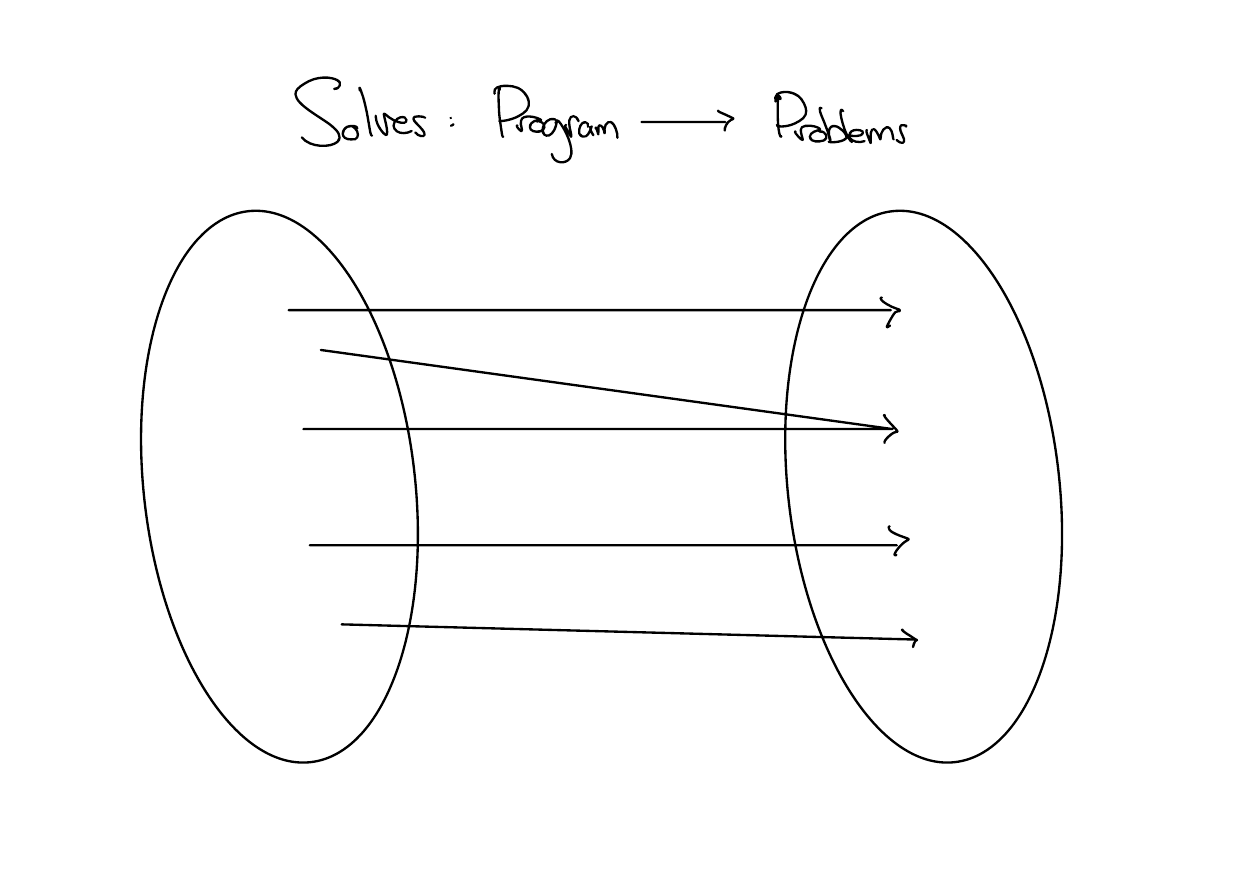
Formalizing the question - Solves
Let Solves: Programs \(\to\) Strings be the function that maps each program to the problem it solves. Since each program solves at most one problem, this function is well-defined.
Our question about whether or not computers can solve all problems is the question of whether or not Solves is…
surjective!Proof (Picture)
Proof - There is a problem that computers can’t solve
Proof.
The answer to our original question is no - computers cannot solve all problems! We will prove this by showing that Solves is not surjective.
By contradiction, assume Solves: Programs \(\to \wp(\)Strings\()\) is surjective. The strategy will be to construct a surjective function from Strings\(\to \wp(\)Strings\()\) which contradicts Cantor’s Theorem.
Let \(f:\)Strings\(\to \wp(\)Strings\()\) be defined as follows
\[f(w) = \begin{cases} \text{Solves}(w) & w \in \text{Programs} \\ \emptyset & \text{else} \end{cases} \]
We claim that \(f\) is surjective. Let \(b \in \wp(\)Strings\()\), since Solves is surjective, there is some program \(a\) such that Solves\((a) = b\). Since Programs\(\subseteq\) Strings, \(a \in\) Strings. By the definition of \(f\), \(f(a) =\) Solves\((a) = b.\) Thus, \(f\) is surjective, contradicting Cantor’s Theorem.
Since we have reached a contradiction, the assumption must have been false. Therefore, Solves is not surjective.There is a problem that computers can’t solve
What are your questions?
FAQ
- “How many problems can/can’t computers solve?”
- “What is a problem we can’t solve with computers?”
- “How can we tell if computers can or can’t solve a problem?”
- “Some problems can be solved and others can not - so some problems are computationally”harder” than others. Are there more ways to compare how computationally hard problems are?”
Additional Notes
- ‘hits’ in the definitions of injective/surjective/bijective is not standard terminology. The standard way to express the same meaning is to use the word ‘preimage.’ In your proofs, you should use the formal FOL definitions.
- The visual part of the proof of Cantor’s Theorem is a little misleading. It makes an additional assumption that you can list the elements of \(A\) using the natural numbers \((\mathbb{N})\) (this property is called ‘countable’). But this is not true for all sets! For example, apply Cantor’s Theorem to \(\mathbb{N}\) to show that \(\wp(\mathbb{N})\) can not be listed using the natural numbers!
- Cantor’s Theorem is fundamental and deep. In particular, it implies that there are bigger and smaller infinities (!). I.e., the powerset of an infinite set is strictly bigger. The powerset of that set is strictly bigger again, and so on. If this interests you, take a class on Set Theory!