Lecture 05: Recurrences 1

2025-06-04

Recurrences

Recurrences

A recursive function is one that depends on itself. Here are some examples.

• \(F(n) = F(n-1) + 1\)
• \(F(n) = 2F(n-1) + 1\)
• \(F(n) = F(n-1) + F(n-2)\)
• \(F(n) = 2F(n/2) + n\)
• \(F(n) = F(n/2) + 1\)
• \(F(n) = 2F(n-2) + F(n-1)\)
• ...

Recursive ambiguity

There can be many functions that satisfy a single recurrence relation, for example, \(F(n) = n + 5\) and \(F(n) = n + 8\) both satisfy

\[ F(n) = F(n-1) + 1 \]

Thus, to specify a recursive function completely, we need to give it a (some) base case(s). I.e.

\[ F(n) = \begin{cases} 5 & n = 0 \\ F(n-1) + 1 & n > 0 \end{cases} \]

Specifies the function \(F(n) = n + 5\).

Why do we care about recurrences?

• The runtime of recursive programs can be expressed as recursive functions.

• Expressing something recursively is often an easier than expressing something explicitly.

The problem with recurrences

Here’s the bad news. It’s hard to answer questions like the following.

If \[ F(n) = \begin{cases} 2 & n=0 \\ 7 & n=1 \\ 2F(n-2) + F(n-1) + 12 & n > 1, \end{cases} \]

what is \(F(100)\)?

We could do it - it would just take a while. Also, it is not immediately obvious what the asymptotics are. As computer scientists, we care about asymptotics. A lot.

Recursive to Explicit

Thus, once we have modelled something as a recurrence, it’s still useful to convert that to an explicit definition of the same function.

Actually, since we’re computer scientists, what we really care about is the asymptotics - we usually don’t need a fully explicit expression.

Recursive to Explicit Examples

What is the explicit formula for \[ F(n) = \begin{cases} 1 & n = 0 \\ 2F(n-1) & n \geq 1 \\ \end{cases} \]

Solution

\(F(n) = 2^n\).

How can we prove it? By induction!

---

\[ F(n) = \begin{cases} 1 & n = 0 \\ 2F(n-1) & n \geq 1 \\ \end{cases} \]

Solution

Claim. \(F(n) = 2^n\).

Base case. The base case holds because \(F(0) = 2^0 = 1\).

Inductive step. Let \(k \in \mathbb{N}\) be any natural number and assume \(F(k) = 2^k\). Then we have

\[ F(k+1) = 2\cdot F(k) = 2\cdot 2^{k} = 2^{k+1}, \]

where the first inequality holds by the recursive definition of \(F\) and then second holds by the inductive hypothesis.

---

What is the explicit formula for \[ F(n) = \begin{cases} 4 & n = 0 \\ 3 + F(n-1) & n \geq 1 \\ \end{cases} \]

Solution

\(F(n) = 4 + 3n\)

---

What is the explicit formula for \[ F(n) = \begin{cases} 1 & n = 0 \\ -F(n-1) & n \geq 1 \\ \end{cases} \]

Solution

\(F(n) = (-1)^n\)

---

What is the explicit formula for \[ F(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ 2F(n-1) - F(n-2) + 2 & n \geq 2 \\ \end{cases} \]

Solution

Claim. \(F(n) = n^2\).

Proof

\(F(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ 2F(n-1) - F(n-2) + 2 & n \geq 2 \\ \end{cases}\)

Solution

Base case. The base cases hold because \(F(0) = 0 = 0^2\), and \(F(1) = 1 = 1^2\).

Inductive step. Let \(k \in \mathbb{N}\) be any natural number with \(k \geq 1\). Assume \(F(i) = i^2\) for all \(i \in \mathbb{N}, i \leq k\). We’ll show \(F(k+1) = (k+1)^2\). By the definition of \(F\), we have

\[ \begin{align*} F(k+1) & = 2F(k) - F(k-1) + 2 \\ & = 2k^2 - (k-1)^2 + 2 \\ & = 2k^2 - k^2 + 2k - 1 + 2 \\ & = (k+1)^2 \end{align*} \]

as required.

The functions we care about

Let’s always imagine the function in question is the runtime of some algorithm. I.e., it maps the size of the input to the running time of the algorithm. Thus, we assume it has the following properties.

• domain \(\mathbb{N}\).

• codomain \(\mathbb{R}_{> 0}\). An algorithm can’t take negative time

• non-decreasing. An algorithm shouldn’t get faster for larger inputs.

Asymptotics Review

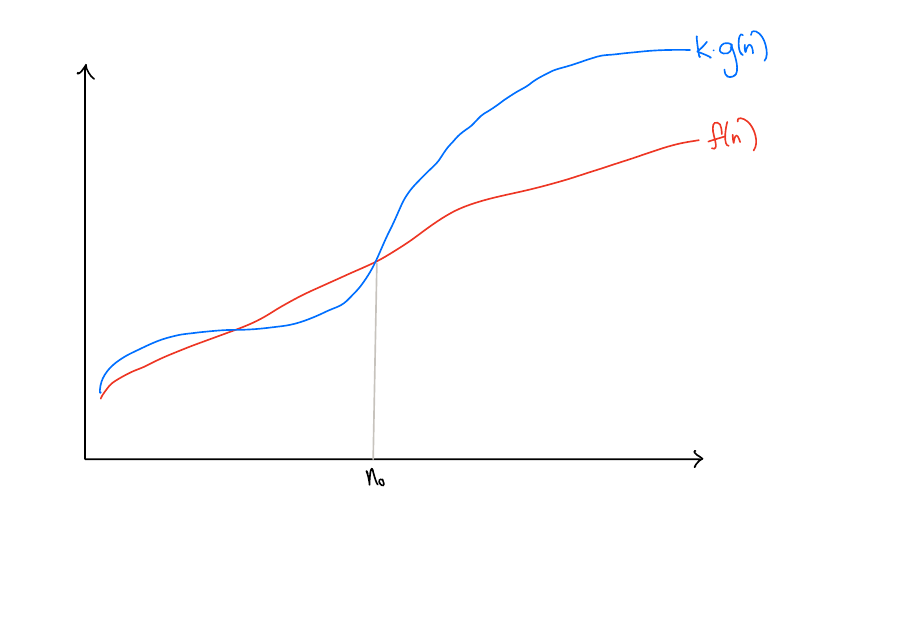
Big-O

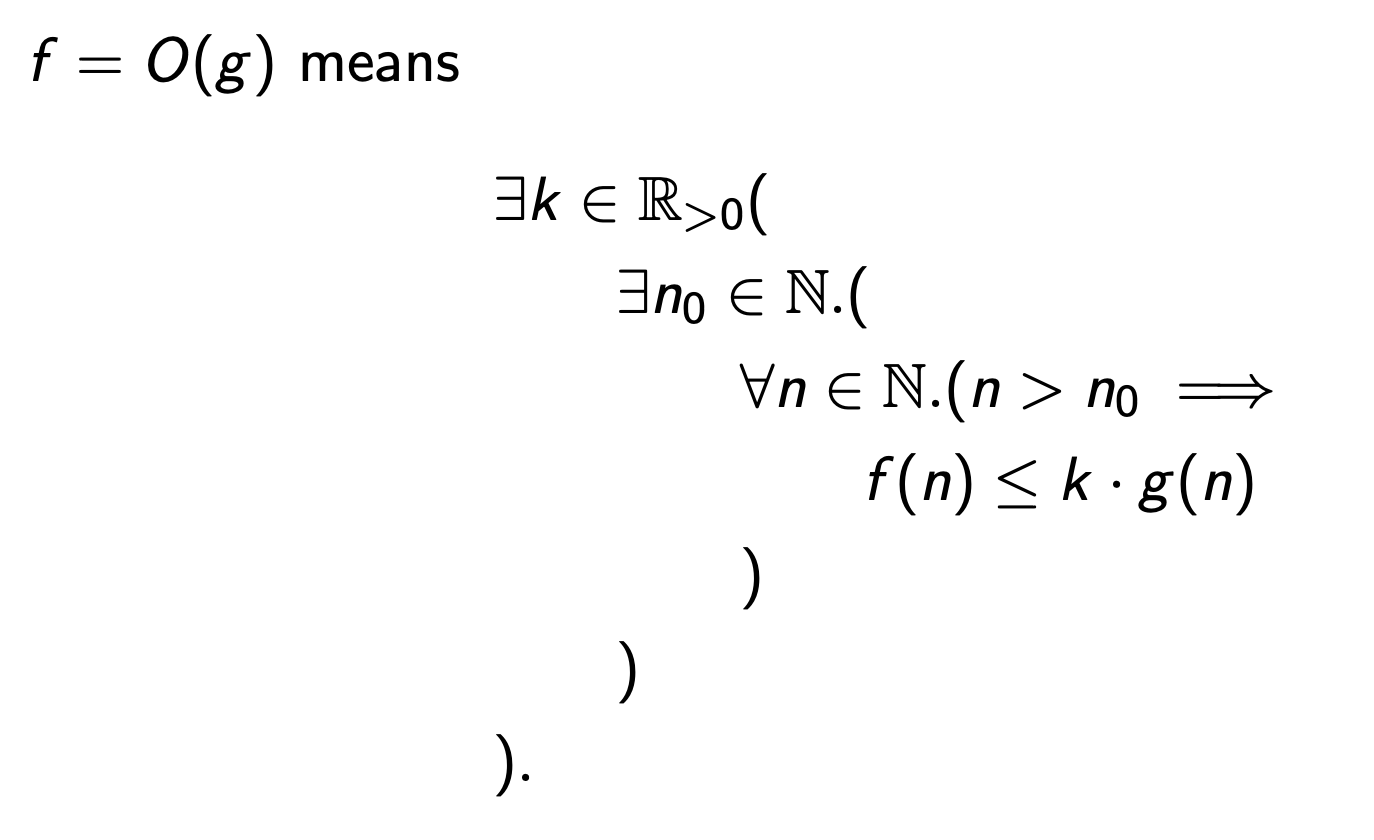
Less formally, \(f\) is at most \(kg(n)\) for large enough inputs, where \(k\) is some constant.

---

In the following slides, the differences in the formal definitions from Big-O are highlighted in red.

Big-Omega

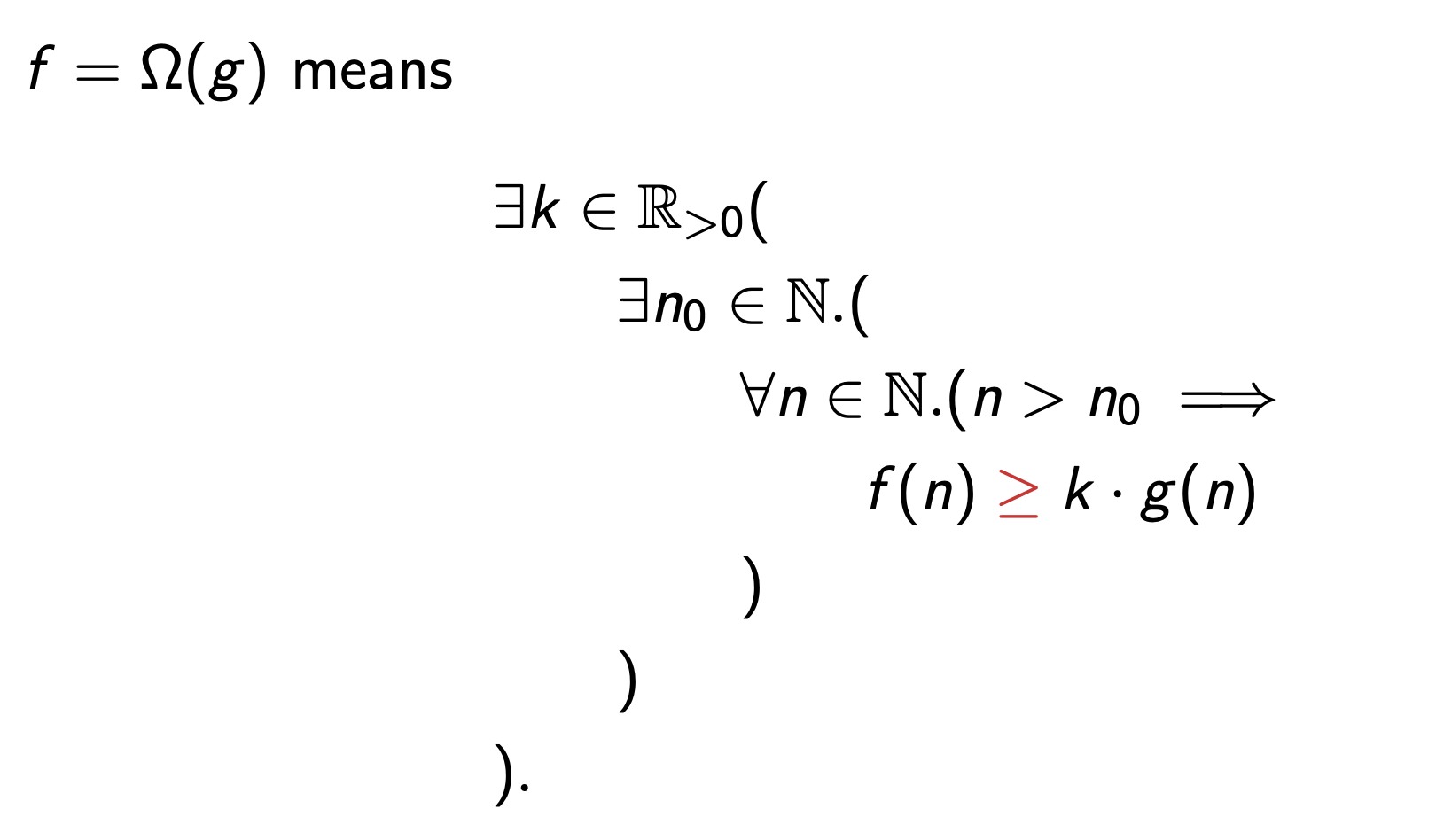
Less formally, \(f\) is at least \(kg(n)\) for large enough inputs, where \(k\) is some constant.

Big-Theta

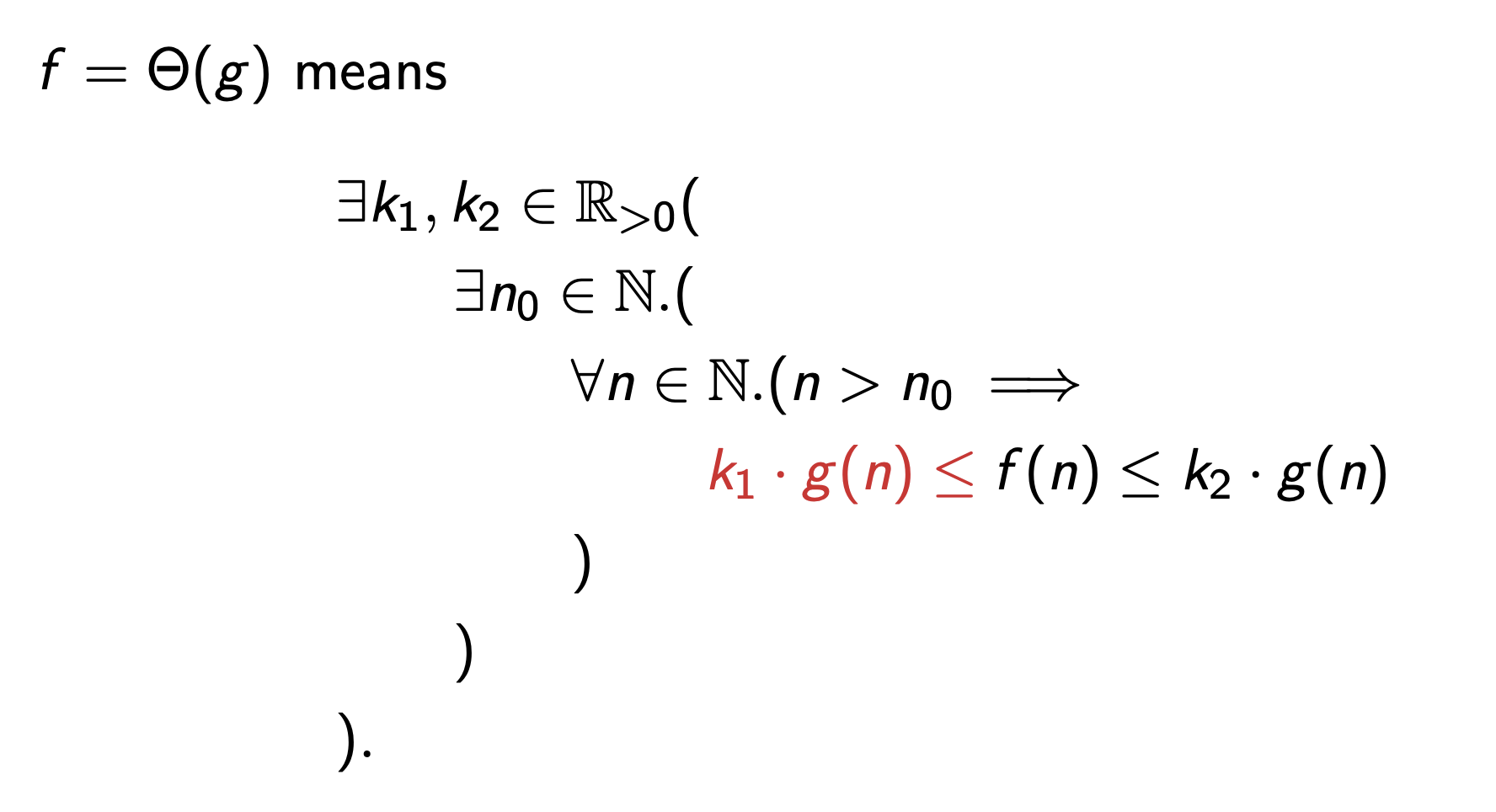
Less formally, \(f\) is between \(k_1\cdot g(n)\) and \(k_2\cdot g(n)\) for large enough inputs, where \(k_1\) and \(k_2\) are some constants.

Equivalently, \(f = O(g)\) and \(f = \Omega(g)\).

Little-o

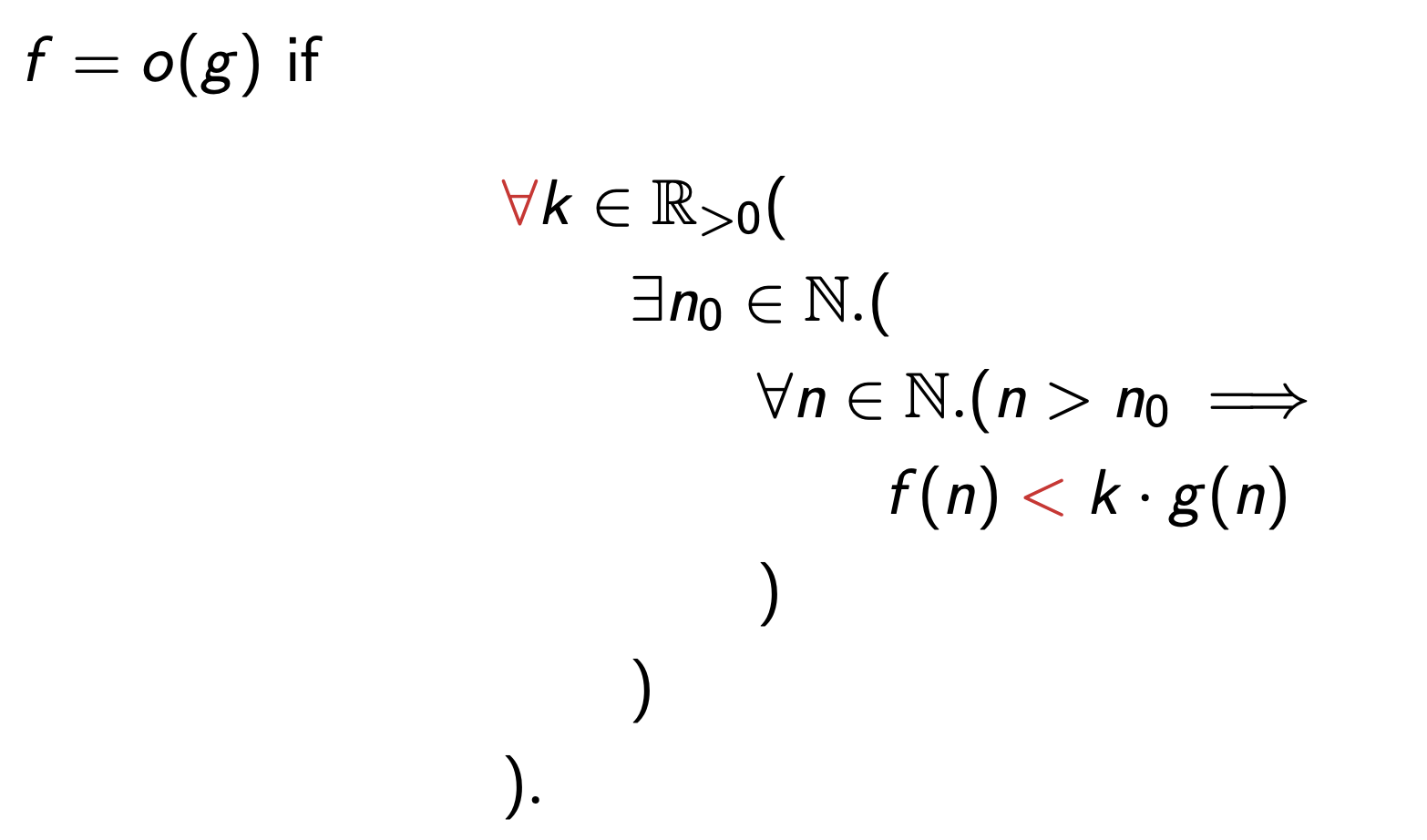
Less formally, no matter how small a constant \(k\) I multiply \(g\) by, for all large enough inputs, \(f(n)\) is less than \(g(n)\).

Little-omega

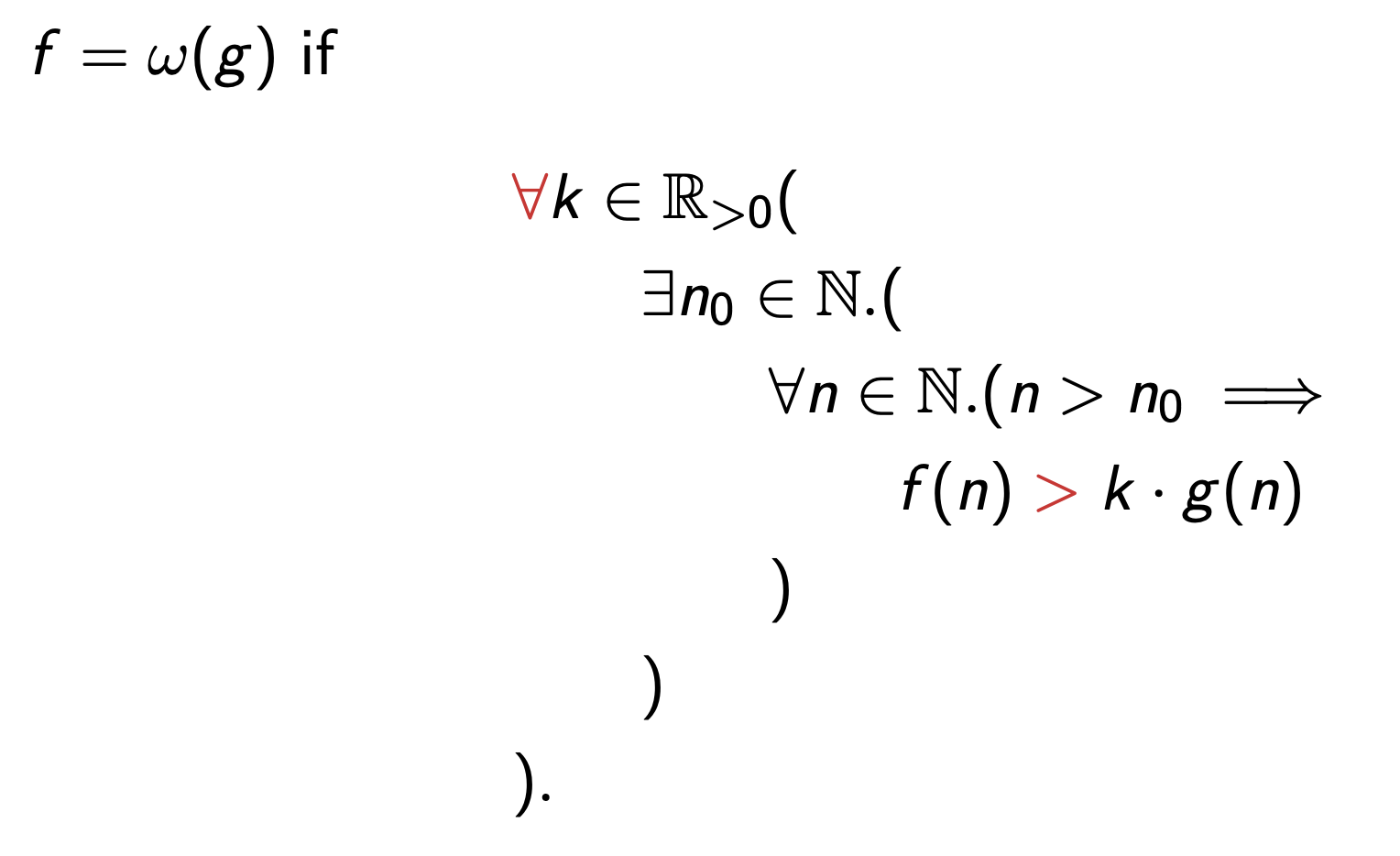
Less formally, no matter how large a constant \(k\) I multiply \(g\) by, for all large enough inputs, \(f(n)\) is greater than \(g(n)\).

A note about the definitions

There is some flexibility in these definitions. I.e. You can replace \(<\) with \(\leq\) and \(>\) with \(\geq\) (and vice versa) wherever your want.

You can also change the side the constant \(k\) is multiplied on if you want. I.e. multiply \(k\) to \(f\) instead of \(g\).

It’s a good exercise to prove this.

Asymptotics and orders

We can think of these asymptotics relations as

• \(f = o(g)\) is like \(f < g\)

• \(f = O(g)\) is like \(f \leq g\)

• \(f = \Theta(g)\) is like \(f \approx g\)

• \(f = \Omega(g)\) is like \(f \geq g\)

• \(f = \omega(g)\) is like \(f > g\)

We’ll sometimes use \(\prec, \preceq, \approx, \succeq, \succ\) for \(o, O, \Theta, \Omega, \omega\) respectively.

Logs in this class

\(\log\) in this class is always \(\log_2\) unless otherwise specified. It is the true inverse of the the function that maps \(x \mapsto 2^x\). I.e., for any \(x \in \mathbb{R}\).

\[ \log(2^x) = x, \]

and for any \(y \in \mathbb{R}_{>0}\)

\[ 2^{\log(y)} = y. \]

Fast Rules

\[ 1 \prec \log(n) \prec n^{0.001} \prec n \prec n \log(n) \prec n^{1.001} \prec n^{1000} \prec 1.001^n \prec 2^n \]

Helpful alternative definition for little-o if you know limits:

\[ \lim_{n \to \infty} \frac{f(n)}{g(n)} = 0 \iff f \prec g \]

Dominoes

Dominoes

How many ways are there to tile a \(2 \times n\) grid using \(2\times 1\) dominoes?

Examples

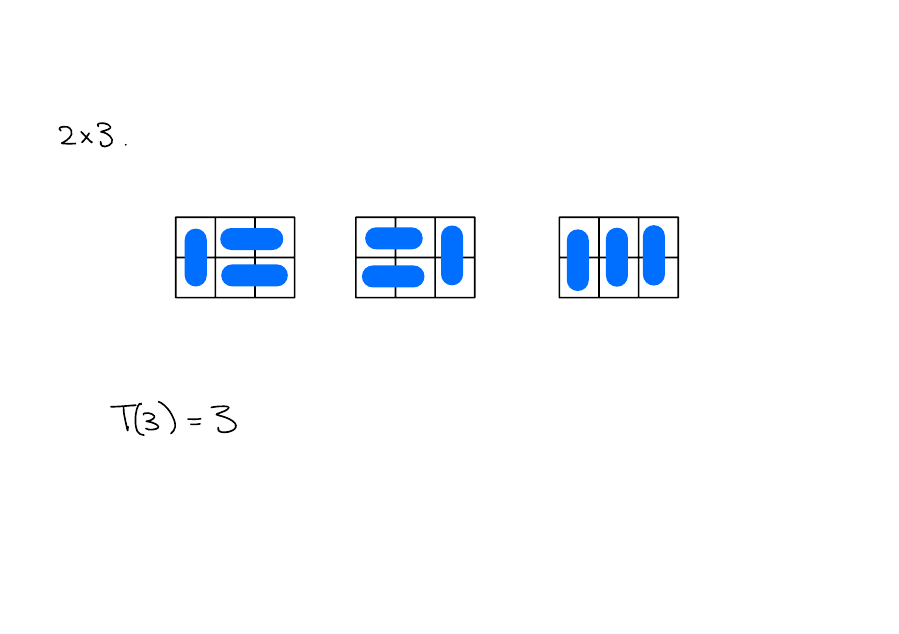
Number of tilings

Let \(T(n)\) be the number of tilings of a \(2\times n\) grid using \(2\times 1\) dominoes.

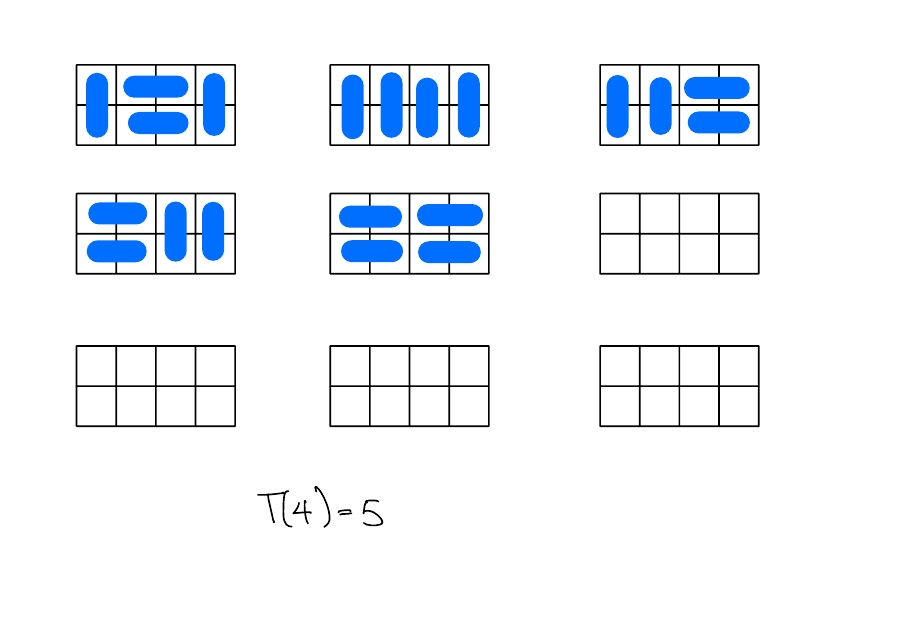
\(T(4)\)

Solution

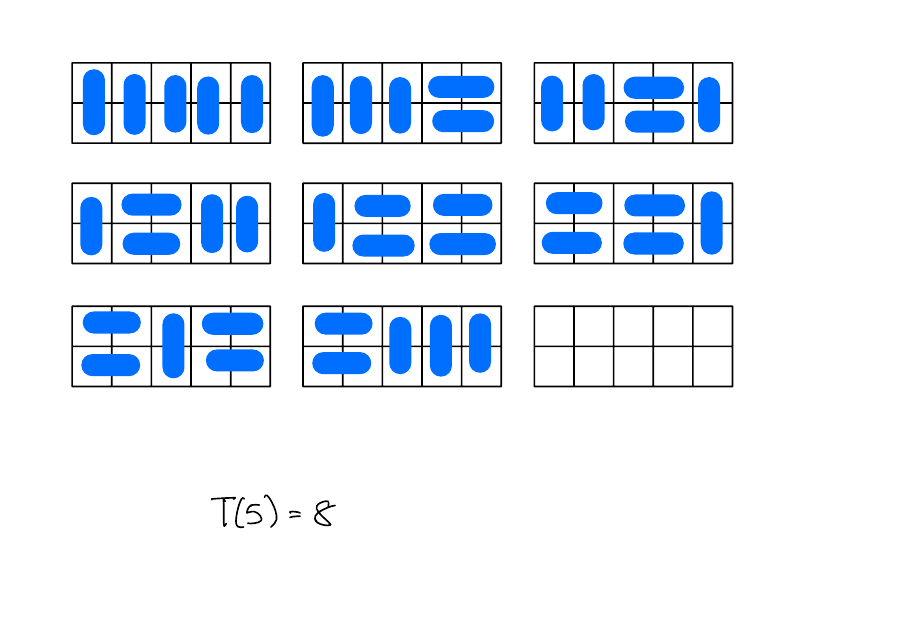
\(T(5)\)

Solution

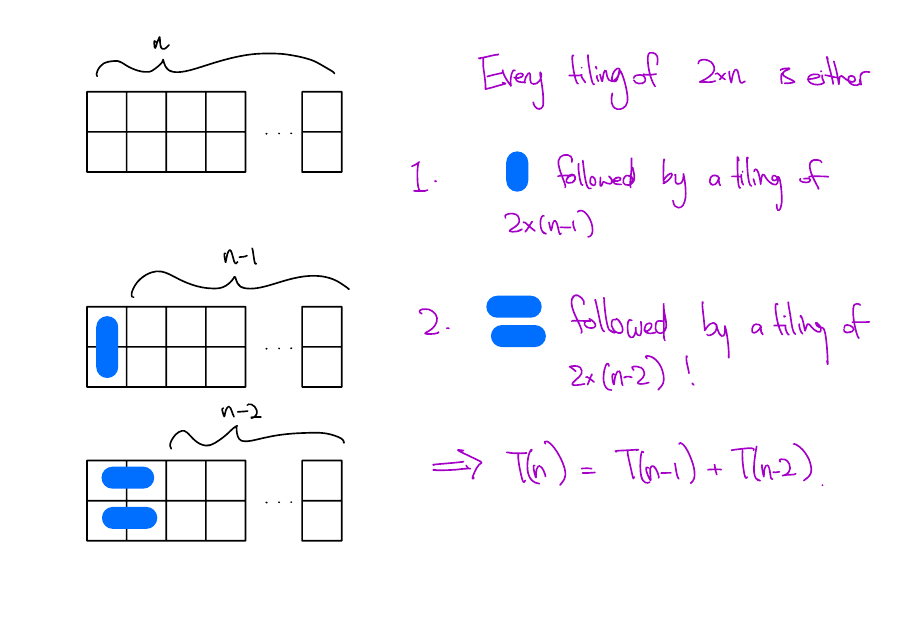
Number of tilings - Recursively

Fibonacci Numbers

\[ \mathrm{Fib}(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ \mathrm{Fib}(n-1) + \mathrm{Fib}(n-2) & n \geq 2 \\ \end{cases} \]

We’ll now study the asymptotics of \(\mathrm{Fib}(n)\).

Note that \(T(n)\) and \(\mathrm{Fib}(n)\) have the same recursive relation. \(T(n)\) are just the Fibonacci numbers shifted by one. I.e. \(T(n) = \mathrm{Fib}(n+1)\).

An upper bound

Claim. \(\forall n \in \mathbb{N}. (F(n) \leq 2^n)\)

Solution

Base case. \(\mathrm{Fib}(0) = 0 \leq 2^0 = 1\), and \(\mathrm{Fib}(1) = 1 \leq 2^{1} = 2\). Thus the base case holds.

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume \(\mathrm{Fib}(i) \leq 2^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \leq 2^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k+1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \leq 2^{k} + 2^{k-1} & (IH) \\ & \leq 2^{k} + 2^{k} \\ & = 2^{k+1} \end{align*} \]

so we’re done.

Tightening the analysis

Look at the previous proof. Where was there a lot of slack in the analyis?

Solution

The inequality \(2^k + 2^{k-1} \leq 2^k + 2^k\) is pretty loose!

---

Let’s try the same proof with \(1.8=9/5\) instead of 2, does it still work? (Forget the base case for now).

Solution

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume \(\mathrm{Fib}(i) \leq 1.8^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \leq 1.7^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k+1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \leq 1.8^{k} + 1.8^{k-1} & (IH) \\ & = 1.8^{k}(1 + 5/9) \\ & \leq 1.8^{k}(1.56) \\ & \leq 1.8^{k+1} \\ \end{align*} \]

so we’re done.

---

Let’s try the same proof with \(1.5 = 3/2\) instead, does that still work? (Forget the base case for now).

Solution

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume \(\mathrm{Fib}(i) \leq 1.5^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \leq 1.5^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k+1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \leq 1.5^{k} + 1.5^{k-1} & (IH) \\ & = 1.5^{k}(1 + 2/3) \\ & \leq 1.5^{k}(1.67) \\ \end{align*} \]

but 1.67 \(\not \leq 1.5\), so we can’t say \(1.5^{k}(1.67) \leq 1.5^{k+1}\).

---

The real answer must be somewhere in between \(1.5^n\) and \(1.8^n\)!

Fibonacci

Check out this graph

Optimizing the base

Solution

Let’s run the proof this time with the base of the exponent as a variable \(x\). Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume \(\mathrm{Fib}(i) \leq x^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \leq x^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k+1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \leq x^{k} + x^{k-1} & (IH) \\ & = x^{k}(1 + 1/x) \end{align*} \]

To prove the inductive step, we need \(x^k(1 + 1/x) \leq x^{k+1}\). I.e. \(x^k + x^{k-1} \leq x^{k+1}\) dividing through by \(x^{k-1}\) and rearranging, we need \(x^2 - x - 1 \geq 0\). Finding the minimum value of \(x\) for which this happens will give us a tight bound on the base. Solving this quadratic, we find that \(x \geq \frac{1 + \sqrt{5}}{2}\) or \(x \leq \frac{1 - \sqrt{5}}{2}\).

Note that this means \(\varphi^2 - \varphi - 1 = 0\), or \(\varphi^2 = \varphi + 1\).

So the smallest positive value for \(x\) that makes this happen is \(\frac{1 + \sqrt{5}}{2} \approx 1.618\). This value has a name and is called \(\varphi\) ‘phi’ or the ‘golden ratio’.

Upper bound

Claim. \(\forall n \in \mathbb{N}. (\mathrm{Fib}(n) \leq \varphi^n)\)

Solution

Base case. \(\mathrm{Fib}(0) = 0 \leq \varphi^0 = 1\), and \(\mathrm{Fib}(1) = 1 \leq \varphi^{1} \approx 1.618\). Thus the base case holds.

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume \(\mathrm{Fib}(i) \leq \varphi^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \leq \varphi^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k+1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \leq \varphi^{k} + \varphi^{k-1} & (IH) \\ & \leq \varphi^{k-1}(\varphi + 1) \\ & = \varphi^{k-1}\varphi^2 & (\varphi^2 = \varphi + 1) \\ & = \varphi^{k+1} \\ \end{align*} \]

so we’re done.

A lower bound

Solution

The previous slide shows that \(\mathrm{Fib}(n) = O(\varphi^n)\), we’ll show here that \(\mathrm{Fib}(n) = \Omega(\varphi^n)\). In particular, for all \(n \in \mathbb{N}, n \geq 1. (\mathrm{Fib}(n) \geq 0.3\cdot \varphi^n)\)

Base case. For the base cases we have \(\mathrm{Fib}(1) = 1 \geq 0.3 \cdot \varphi \approx 0.48\), \(\mathrm{Fib}(2) = 1 \geq 0.3\cdot \varphi^2 \approx 0.78\)

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 2\), and assume \(\mathrm{Fib}(i) \geq 0.3\varphi^i\) for all \(i \leq k\), we’ll show \(\mathrm{Fib}(k + 1) \geq 0.3 \varphi^{k+1}\). We have

\[ \begin{align*} \mathrm{Fib}(k + 1) & = \mathrm{Fib}(k) + \mathrm{Fib}(k-1) \\ & \geq 0.3(\varphi^k + \varphi^{k-1}) & (IH) \\ & = 0.3\varphi^{k-1}(\varphi + 1) \\ & = 0.3\varphi^{k-1}\varphi^2 \\ & = 0.3\varphi^{k+1}. \end{align*} \]

Fibonacci

\(\mathrm{Fib}(n) = \Theta(\varphi^n)\).

The complete answer - Binet’s formula

\[ \mathrm{Fib}(n) = \frac{\varphi^n - (1 - \varphi)^n}{\sqrt{5}} \]

Note that \(1 - \varphi \approx -0.618\), so the \((1 - \varphi)^n\) term goes to zero really quickly and becomes irrelevant.

In fact, since \(|(1 - \varphi)^n/\sqrt[]{5}|\) is always less than \(1/2\), \(\mathrm{Fib}(n)\) is just \(\frac{\varphi^n}{\sqrt[]{5}}\) rounded to the nearest whole number!

See the suggestions on this slide for further reading on solving recurrences exactly.

Takeaway

You can show the asymptotics of recurrences by induction!

Binary Search

Searching in a sorted array

Inputs:

• A sorted list l

• A target value target

Output: The index of target in l. None if target is not in l.

Binary search intuition

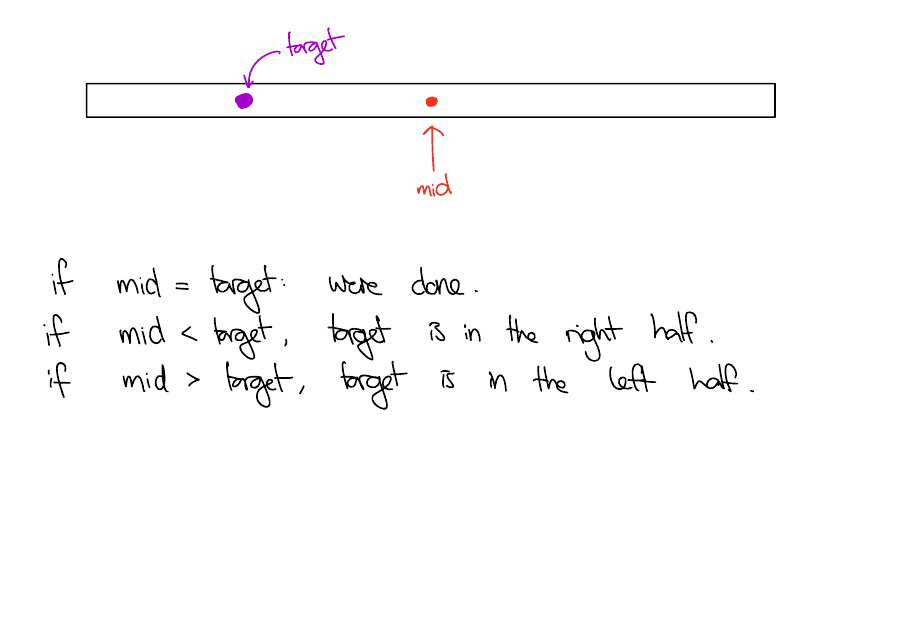
Binary Search

def bin_search(l, t, a, b):
    if b == a:
        return None
    else:
        m = (a + b) // 2
        if l[m] == t:
            return m
        elif l[m] < t:
            return bin_search(l, t, m + 1, b)
        else:
            return bin_search(l, t, a, m)

Searches l between indices a inclusive and b exclusive.

Example

code

Screenshot:

Binary Search

Let \(T_\mathrm{BinSearch}\) be the function that maps the length of the input array to the worst case running time of the binary search algorithm. What is the recurrence for \(T_\mathrm{BinSearch}\)?

Let’s say doing a comparison and returning a value takes 1 unit of work (we could replace this with a constant amount of work \(c\)). The point is, the amount of work required to do these operations does not grow with the array length.

If \(n = 0\) we return None, so \(T_\mathrm{BinSearch}(0) = 1\). In the recursive case, the value in the middle is not equal to the target. One side of the middle has \(\left\lceil (n-1)/2 \right\rceil\) values and the other has \(\left\lfloor (n-1)/2 \right\rfloor\). In the worst case, we call the algorithm recursively on a list of size \(\left\lceil (n-1)/2 \right\rceil = \left\lfloor n/2 \right\rfloor\). Thus, for \(n \geq 1\),

\[ T_\mathrm{BinSearch}(n) = T_\mathrm{BinSearch}(\left\lfloor n/2 \right\rfloor) + 1 \]

Some values

\(n\)	\(T_\mathrm{BinSearch}(n)\)
0	1
1	2
2	3
3	3
4	4
5	4
6	4
7	4
8	5
15	5
16	6

An upper bound

\(T_\mathrm{BinSearch}(n) = T_\mathrm{BinSearch}(\left\lfloor n/2 \right\rfloor) + 1\)

Claim. \(T_\mathrm{BinSearch}(n) = O(n)\). In particular, we claim for all \(n \in \mathbb{N}. n \geq 1, T_\mathrm{BinSearch}(n) \leq n + 1\).

Solution

Base case. \(T_\mathrm{BinSearch}(1) = 2 \leq 1 + 1\).

Inductive step. Let \(k \in \mathbb{N}, k \geq 1\), and assume \(T_\mathrm{BinSearch}(i) \leq i\) for all \(1 \leq i \leq k\). Then we have

\[ \begin{align*} T_\mathrm{BinSearch}(k+1) & = T_\mathrm{BinSearch}(\left\lfloor (k + 1)/2 \right\rfloor) + 1 \\ & \leq \left\lfloor (k+1)/2 \right\rfloor + 2 & (IH) \\ & \leq (k + 1) / 2 + 2 & (\left\lfloor x \right\rfloor \leq x) \\ & \leq 2k/2 + 2 & (k \geq 1) \\ & = (k + 1) + 1 \end{align*} \]

as required.

What should the actual runtime be?

Solution

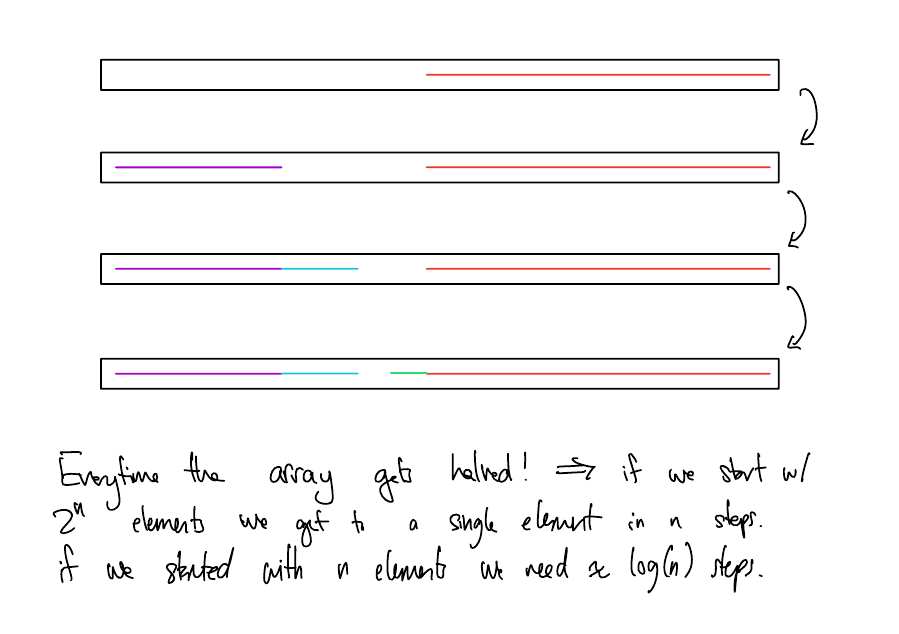
\(T_\mathrm{BinSearch}(n) = O(log(n))\)

\(T_\mathrm{BinSearch}(n) = T_\mathrm{BinSearch}(\left\lfloor n/2 \right\rfloor) + 1\)

Claim: \(T_\mathrm{BinSearch}(n) = O(\log(n))\). In particular, for all \(n \geq 1\), \(T_\mathrm{BinSearch}(n) \leq c\log(n) + d\) where \(c\) and \(d\) are constants that we will pick later.

Proof

Base case. For the base case we have

\[ T_\mathrm{BinSearch}(1) = 2 \leq c\log(1) + d \]

Note that \(\log(1) = 0\) so we will need \(d \geq 2\).

Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 1\). Assume for all \(1 \leq i \leq k\), \(T_\mathrm{BinSearch}(i) \leq c\log(i) + d\). Then we have \[ \begin{align*} T_\mathrm{BinSearch}(k + 1) & = T_\mathrm{BinSearch}(\left\lfloor (k+1)/2 \right\rfloor) + 1 \\ & \leq c\log(\left\lfloor (k+1)/2 \right\rfloor) + d + 1 \\ & \leq c\log((k+1)/2) + d + 1 \\ & = c\log(k+1) - c\log(2) + d + 1 \\ & = c\log(k+1) - c + d + 1 \end{align*} \]

Where we get the second line by the inductive hypothesis, the third by the fact that \(\log\) is increasing and \(\left\lfloor x \right\rfloor \leq x\) for all \(x \in \mathbb{R}\), the fourth by log rules and the fifth by the fact that \(\log(2) = 1\).

We want \[ \begin{align*} c\log(k+1) - c + d + 1\leq c\log(k+1) + d. \end{align*} \]

Which is true, for example, when \(c = 1\). Thus, \(T_\mathrm{BinSearch}(n) = O(\log(n))\)

Tips

Here are some tips for showing \(T(n) = O(f(n))\)

• Try proving \(T(n) \leq cf(n) + d\) for some numbers \(c\) and \(d\). After running the proof go back and figure out what \(c\) and \(d\) need to be for your proof to work.

• Sometimes in the inductive step, you might find it helpful to assume \(k\) is larger that some constant for example, \(k \geq 3\). If this is the case, show \(\forall n \in \mathbb{N}, n \geq 3. T(n) \leq f(n)\), and change the base case! (This is like the \(n^2 \leq 2^n\) example from two lectures ago where we used the assumption that \(k \geq 4\) in the inductive step.)

The exact answer

\(n\)	\(T_\mathrm{BinSearch}(n)\)
1	2
2	3
3	3
4	4
5	4
6	4
7	4
8	5
15	5
16	6

Write any \(n \in \mathbb{N}\) with \(n \geq 1\) as \(2^i + x\) for some \(i \in \mathbb{N}, x\in \mathbb{N}\) with \(x \leq 2^i-1\).

Claim. \(\forall i \in \mathbb{N}, \forall x \in \mathbb{N}, x \leq 2^i - 1. (T_\mathrm{BinSearch}(2^i+x) = i + 2)\)

\(T_\mathrm{BinSearch}(2^i+x) = i + 2\)

Solution

By induction on \(i\).

Base case. For \(i = 0\), we have \(T_\mathrm{BinSearch}(2^0) = T_\mathrm{BinSearch}(1) = 2 = 0 + 2\).

Inductive step. Let \(i \in \mathbb{N}\) be any integer and assume for all \(x \leq 2^i - 1\), \(T_\mathrm{BinSearch}(2^i + x) = i + 2\). Now we consider the \(i + 1\) case. Let \(x \leq 2^{i+1}-1\), then we have

\[ \begin{align*} T_\mathrm{BinSearch}(2^{i+1} + x) & = T_\mathrm{BinSearch}\left(\left\lfloor \frac{2^{i+1} + x}{2} \right\rfloor\right) + 1 \\ & = T_\mathrm{BinSearch}\left(2^i + \left\lfloor \frac{x}{2} \right\rfloor\right) + 1 \\ & = i + 2 + 1 \\ & = (i + 1) + 2, \end{align*} \]

where the third inequality holds by the inductive hypothesis since \(\left\lfloor \frac{x}{2} \right\rfloor \leq 2^i -1\), as \(x \leq 2^{i+1} - 1\). This completes the induction. Note this means \(T_\mathrm{BinSearch}(n) = \left\lfloor \log(n) \right\rfloor+2\) for \(n \in \mathbb{N},n \geq 1\).

Getting a good guess

Making a good guess is important in solving recurrences by induction. We’ll see a method to do this next week.

Additional Notes

If you want a general method for fully solving recurrences, you’ll need to study generating functions and partial fraction decomposition. See chapter 7 of Concrete Mathematics by Don Knuth for an excellent introduction. Or take a class on combinatorics.