Lecture 2: Graphs

2025-05-14

While we wait

  • If you could have any superpower, what would it be?

Recap: Functions

The goal of today’s lecture is to have you see graphs everywhere in the world.

Definitions

Definitions

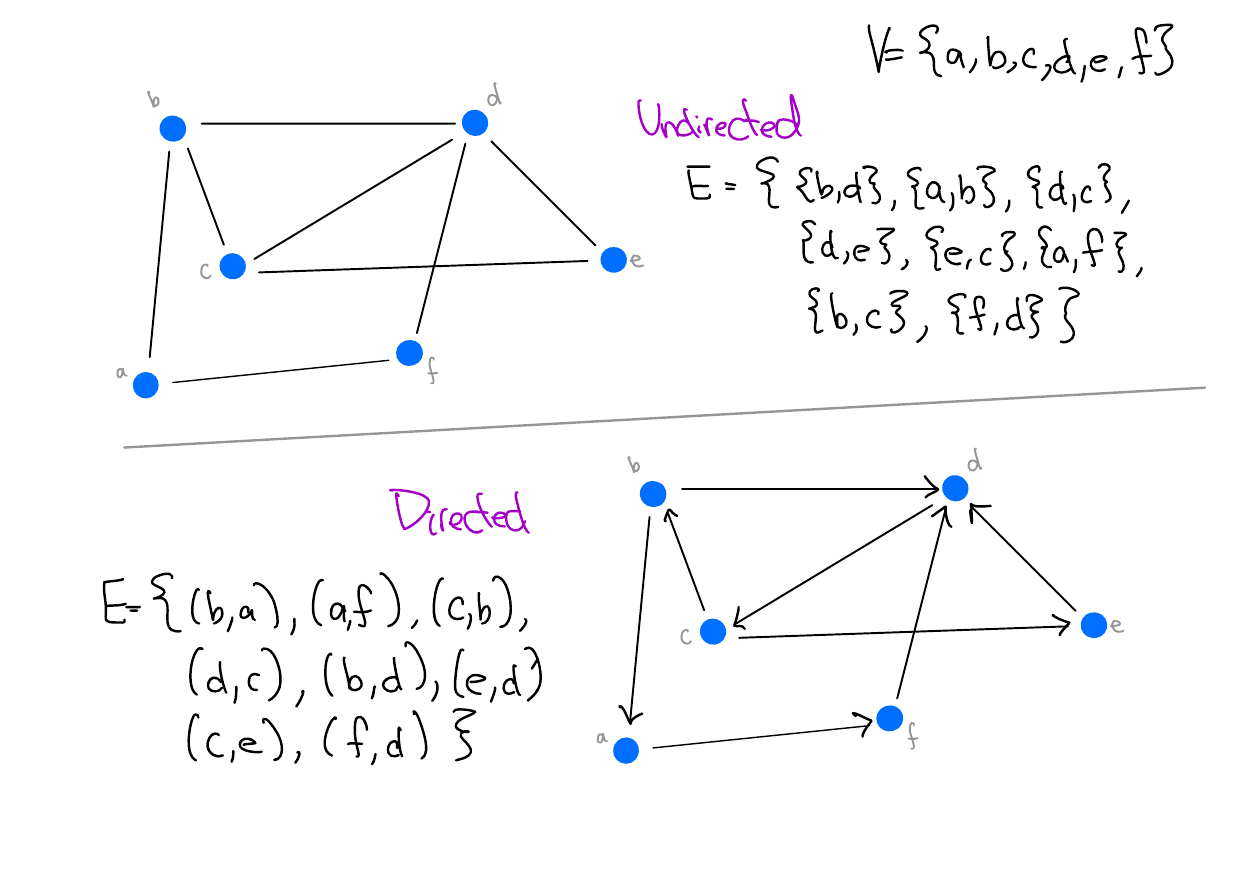
Definition 1 (Graphs) A graph \(G = (V, E)\) is a pair of sets \((V, E)\), where \(V\) is a set of vertices and \(E\) is a set of pairs of vertices.

If \(E\) is a set of unordered pairs, the graph is called undirected, and if \(E\) is a set of ordered pairs, the graph is called directed.

Two vertices \(u, v \in V\) are adjacent if \(\{u, v\} \in E\)

Examples

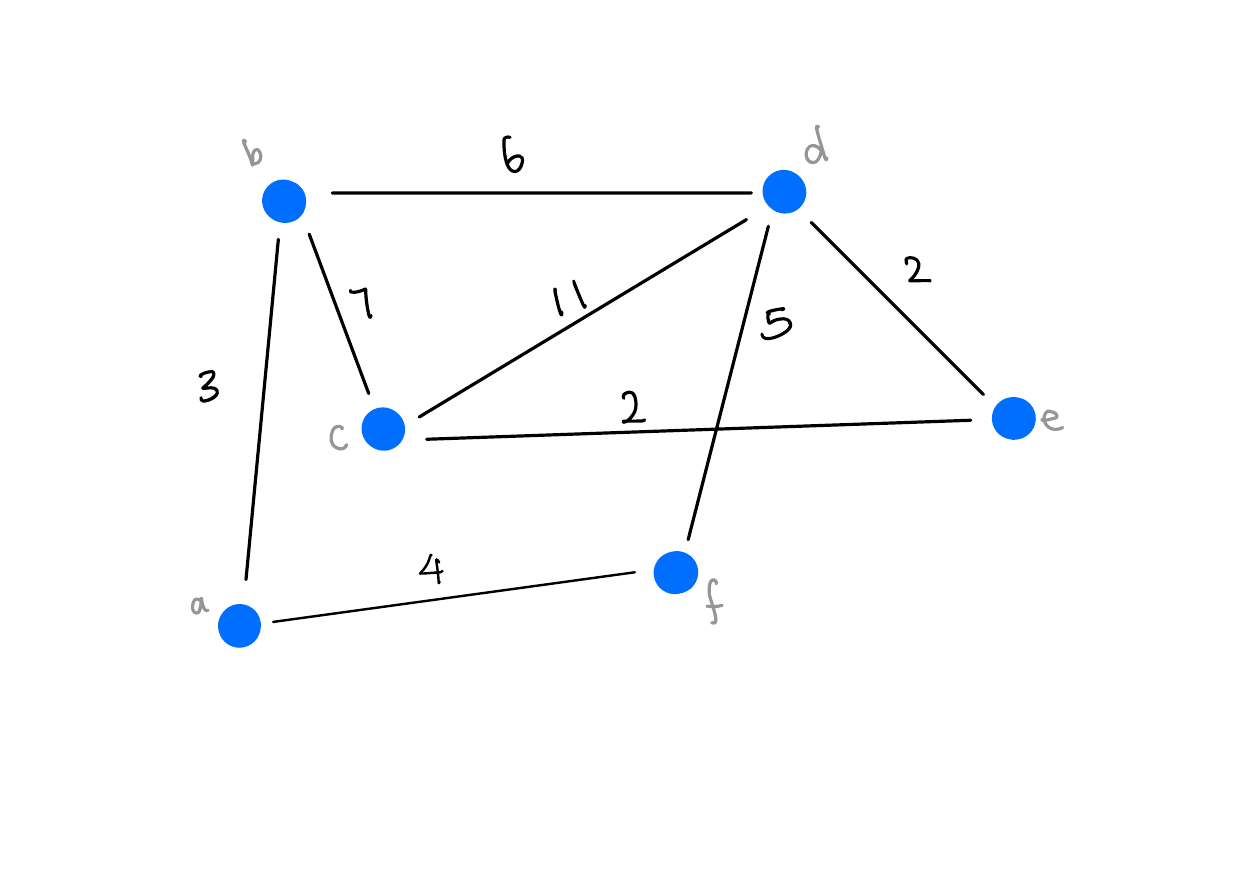
Weights

Seeing graphs everywhere

  • Functions
  • Binary relations
  • Maps
  • Web links
  • Tournament brackets
  • Game trees
  • ...

Modeling with Graphs

An Important Skill

The ability to model real-life problems as graph problems is extremely useful.

You will study algorithms to solve graph problems in CSC373.

Sometimes, modeling the problem is enough, as there are libraries that implement the algorithms for you.

One such library is the networkx (Python). We will see some examples...

Problem 1. Matching

Matching

Definition 2 (Matching) Let \(G = (V, E)\) be a graph. A matching \(M \subseteq E\) is a subset of edges that do not share any endpoints. I.e., every vertex appears in at most one edge in \(M\).

A matching is perfect if every vertex appears exactly once in the matching.

If each edge has a weight, then the weight of a matching is the sum of the weights of edges in \(M\).

Examples

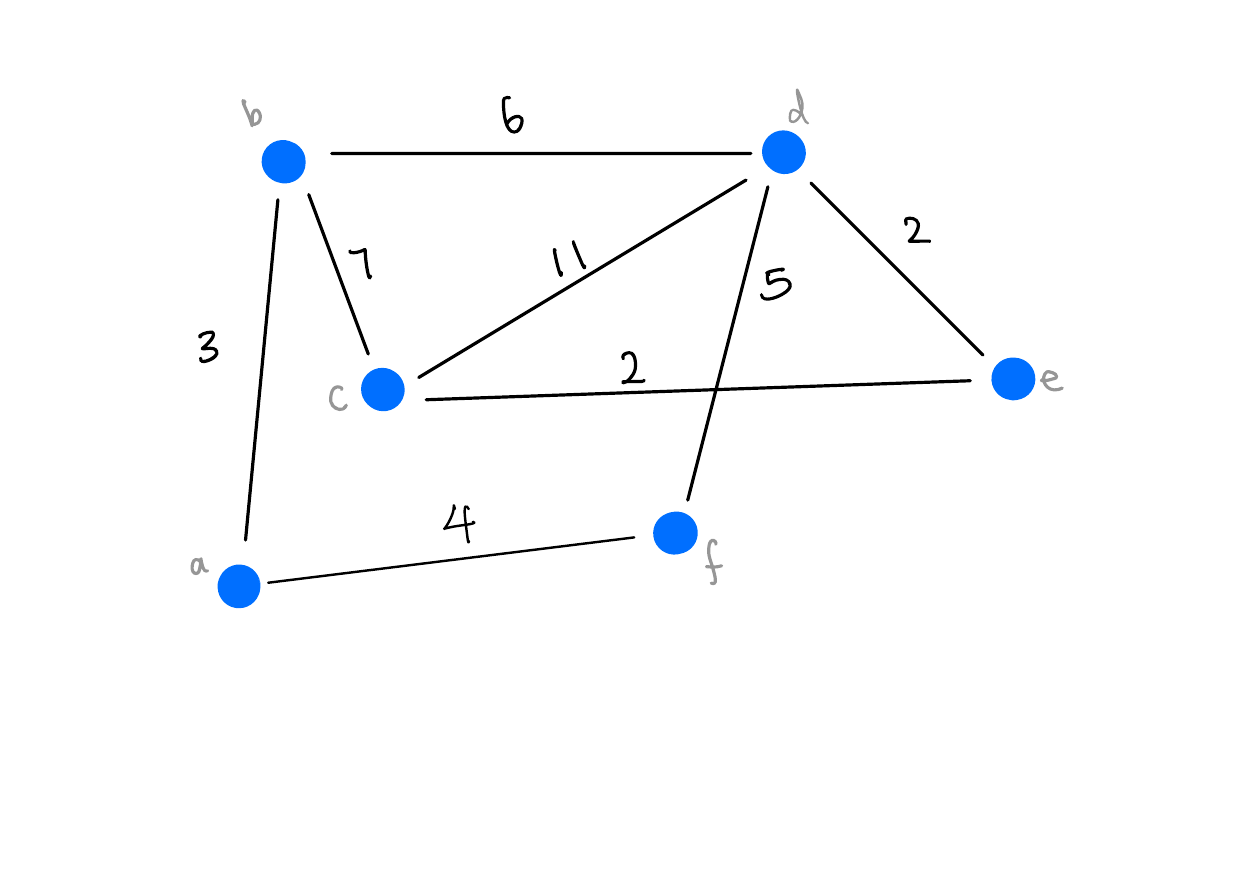
Can you find a matching in the following graph?

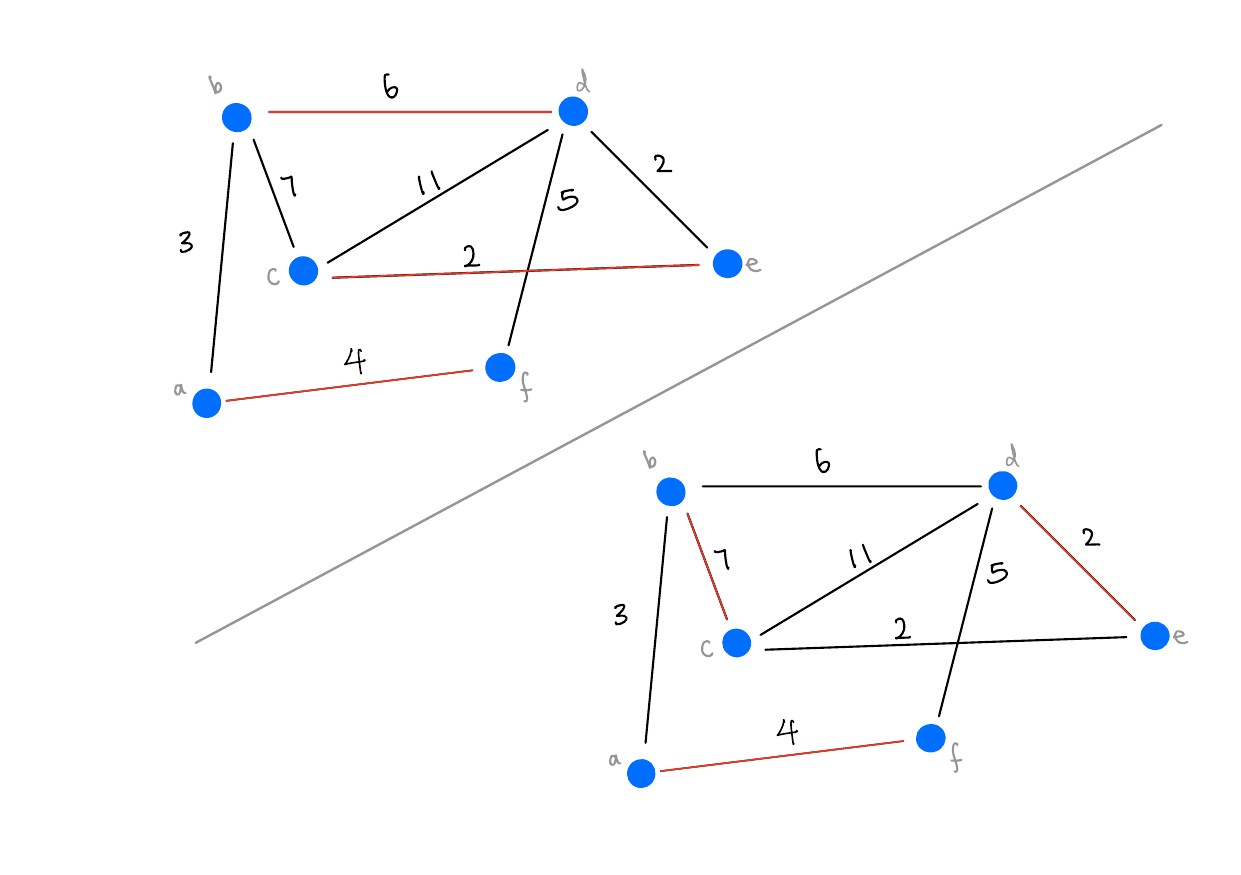
Solution

Matching problem

Input: A graph \(G = (V, E)\).

Output: A matching \(M \subseteq E\).

Usually, we want \(|M|\) to be as large as possible. Sometimes, we also want to maximize or minimize the weight of the matching.

How would you find the maximum matching?

Example: Matchings in the real world

Here’s the setup: There are \(n\) students in a class that need to be matched with partners. Each student fills out a form to indicate a list of times they are available to work and their preference for working in-person or virtually.

Let \(a\), \(b\) be any two distinct students. \(a\) and \(b\) are incompatible if they don’t share any available times.
Otherwise, the compatibility score for \(a\) and \(b\) is the number of time slots in which they overlap in their availability, plus one if they also have the same preference for working in person or virtually.

Your task is to find a pairing with the following properties.

  • Maximizes the number of matched students
  • Maximizes compatibility score.

Modeling as a matching problem.

  • What are the vertices of the graph?
  • What are the edges of the graph?
  • What are the edge weights?
  • What properties of the matching do we want?
Solution
  • Students.
  • There’s an edge if they have a non-zero compatibility score.
  • Compatibility score.
  • We aim for the largest matching (matching as many students as possible) with the highest total compatibility.

Coding

Problem 2. Shortest Path

Paths

Definition 3 (Path) Let \(G = (V, E)\) be a graph. A sequence of distinct vertices \((v_1,...,v_n)\) is a path from \(v_1\) to \(v_n\) if for every \(i \in \{1,...,n-1\}\), \(v_i\) and \(v_{i+1}\) are adjacent. The length of the path is the number of edges in the path.

Example

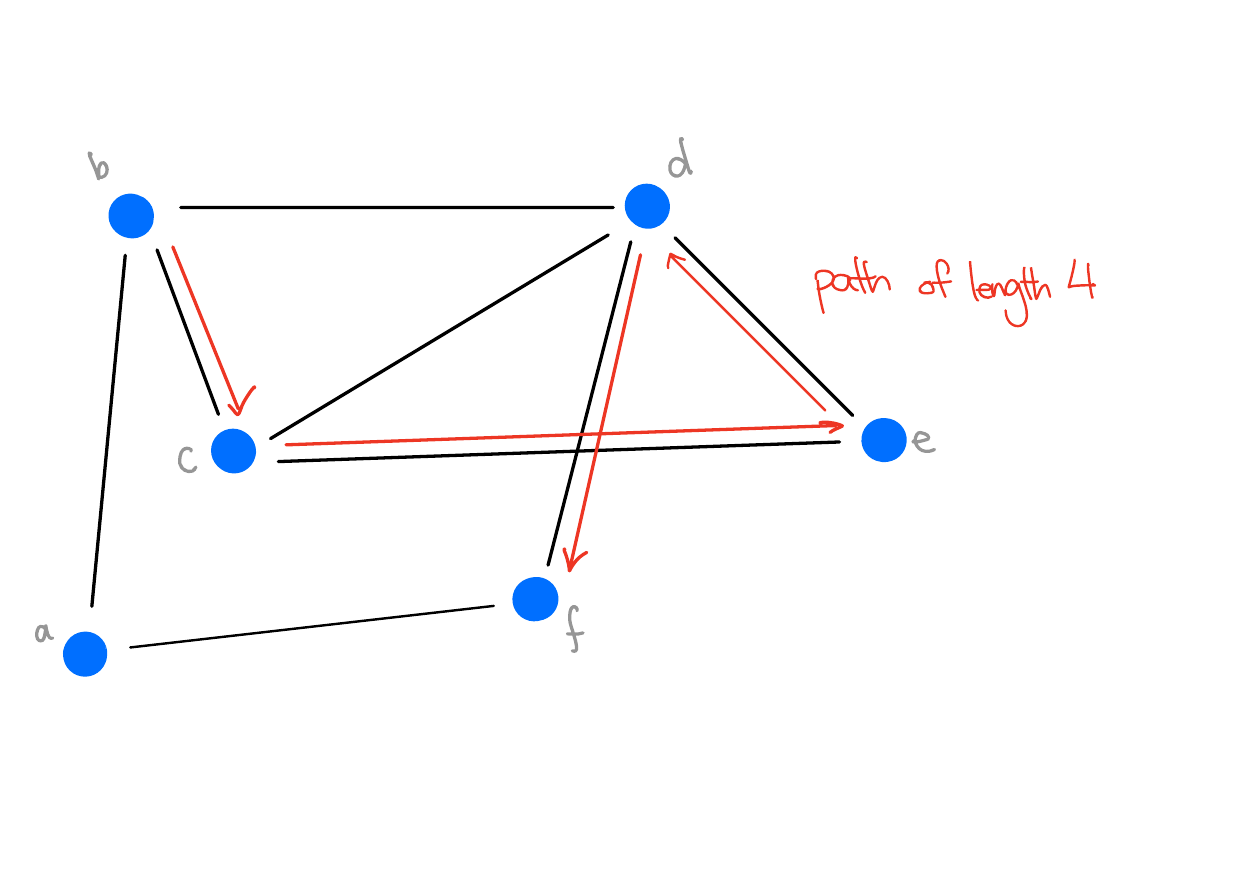
Example

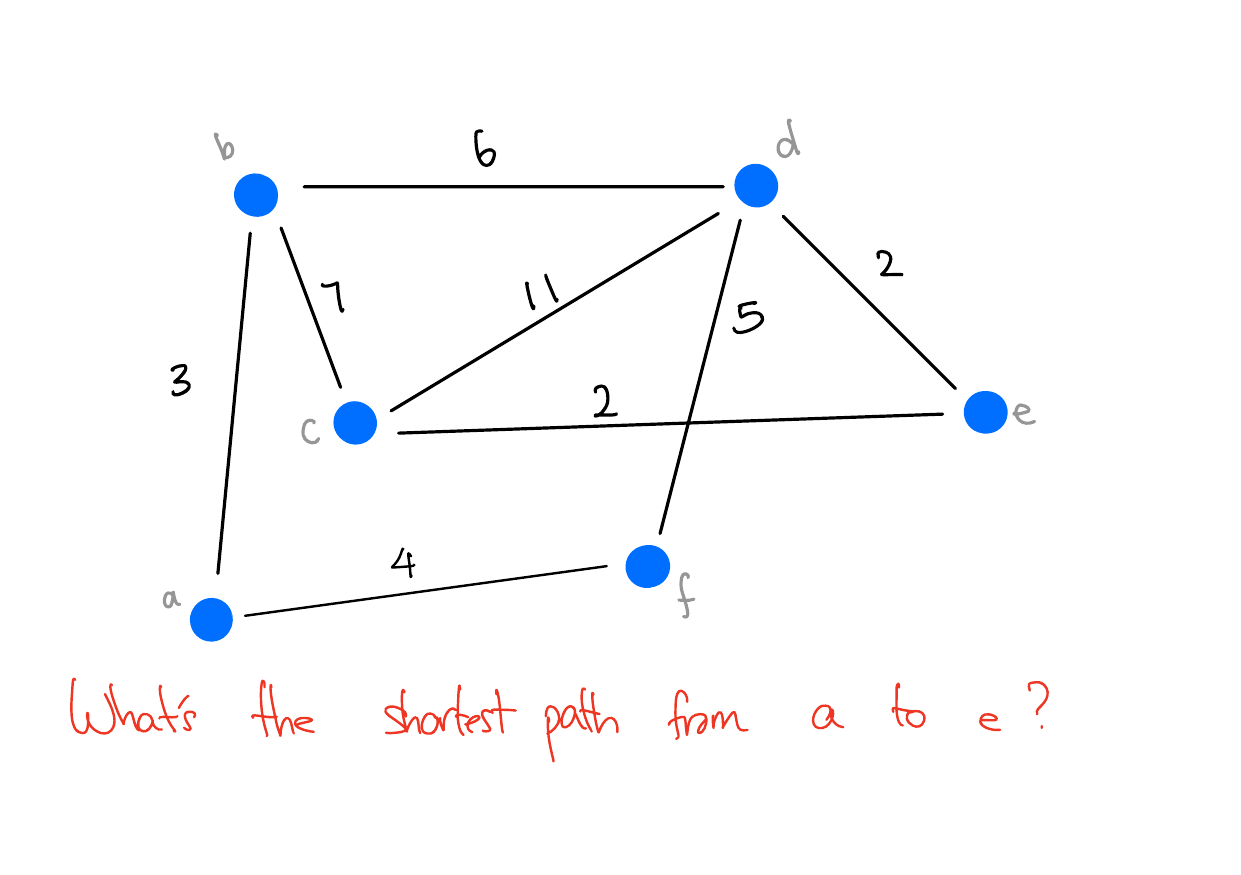
Path Finding Problem

Input: A graph \(G = (V, E)\) and two vertices \(u, v \in V\).

Output: A path from \(u\) to \(v\) in \(G\). I.e. a sequence of vertices \((v_1, v_2,...,v_n)\) where \(v_1 = u\) and \(v_n = v\).

Typically, we want to find the path with the smallest length. If each edge has a weight, we may also want to find the path with the smallest total weight.

Wikipedia Game

Here are the rules:

  • Start with a random article
  • Your goal is to find your way to the University of Toronto wiki page
  • The only way you can move is by clicking on links

Let’s play!

Modeling as a shortest path problem

  • \(V = \{\text{wiki pages}\}\)
  • \(E = \{(u, v) \in V \times V: u \text{ links to } v\}\)

Let \(G = (V, E)\). Then, given a random Wikipedia page \(u\), the shortest path from \(u\) to \(\mathrm{University of Toronto}\) is the optimal solution for the Wikipedia Game.

Problem 3. The Traveling Salesman

Cycles

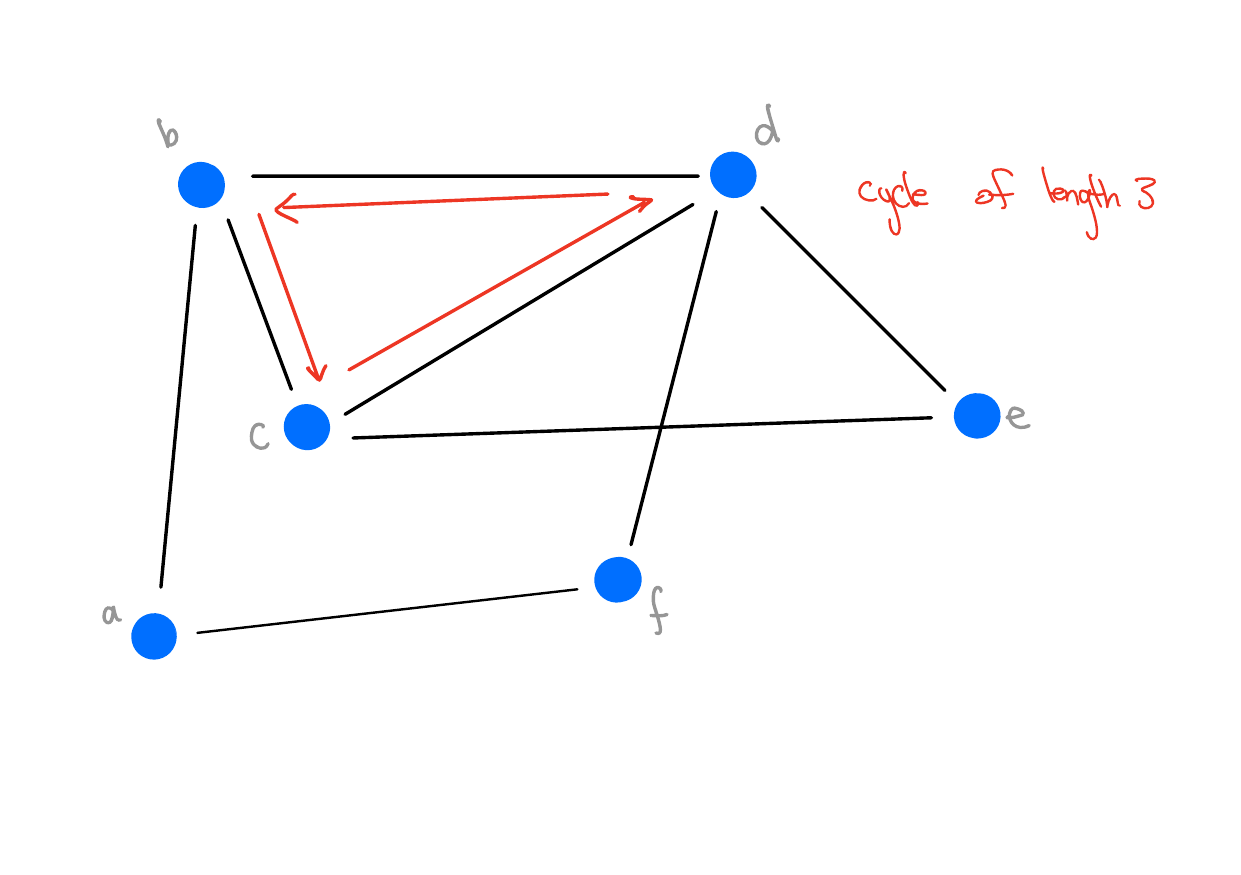
Definition 4 (Cycle) Let \(G = (V, E)\) be a graph

  • A sequence of vertices \((v_1,...,v_n)\), is a cycle if \((v_1,...,v_{n-1})\) is a path, \(v_1 = v_n\), and \(\{v_{n-1}, v_n\} \in E\).

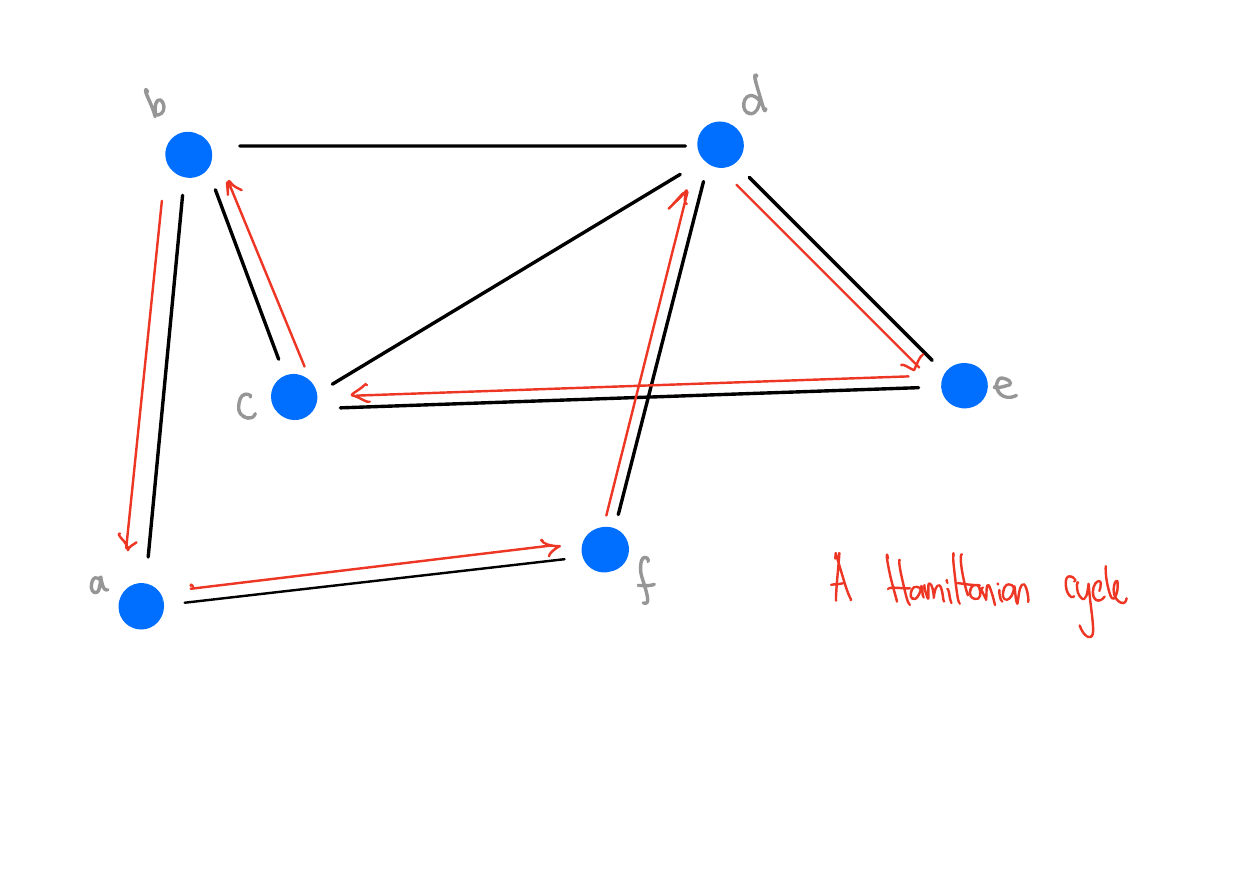
  • A cycle is called Hamiltonian if every vertex in the graph appears in the cycle exactly once (except for the start/end vertex, which appears twice).

The minimum length of a cycle is \(3\) (i.e., \(n \geq 4\)).

Example - Cycle

Example - Hamiltonian Cycle

Traveling Salesman Problem

Input: A graph \(G = (V, E)\) and a starting vertex \(h\)

Output: A Hamiltonian cycle in \(G\) starting from \(h\) that minimizes the total edge weights.

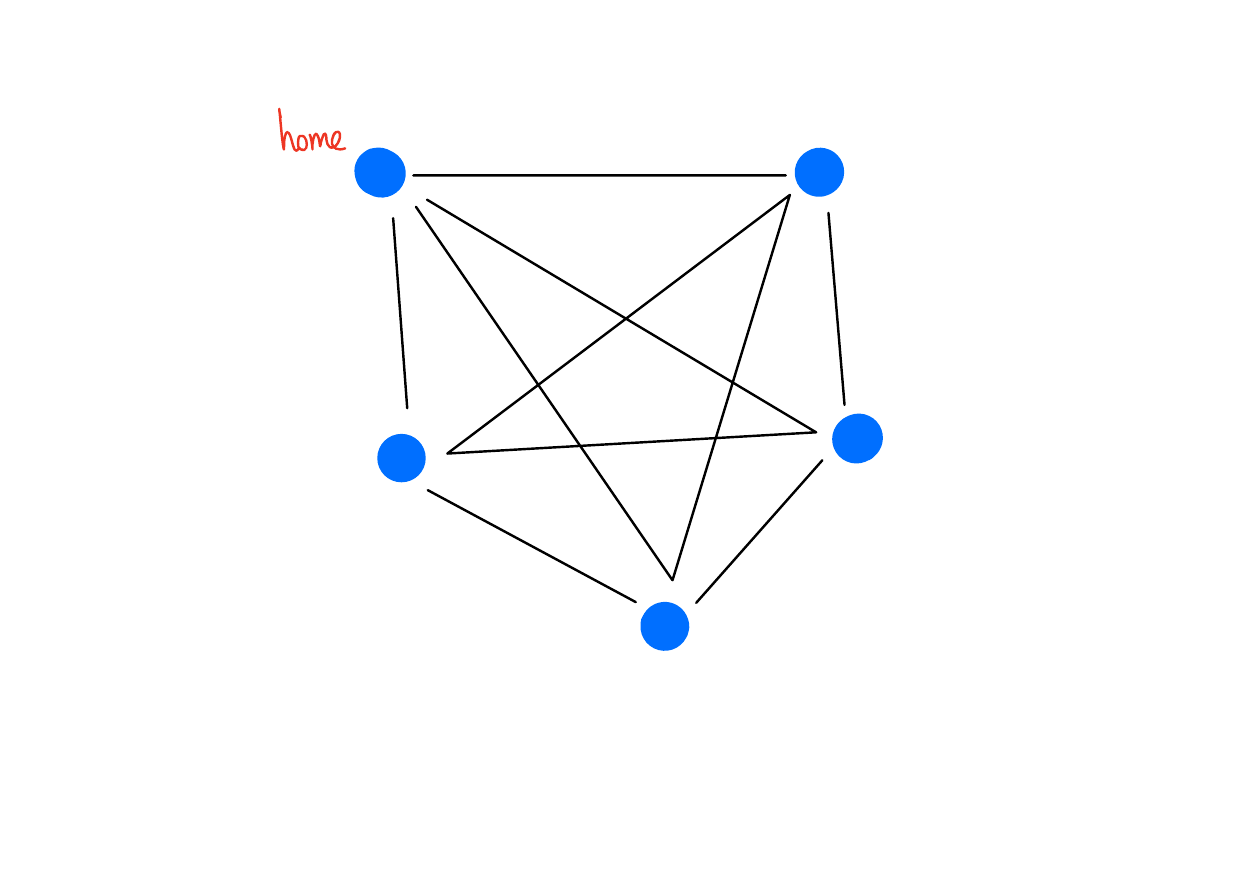
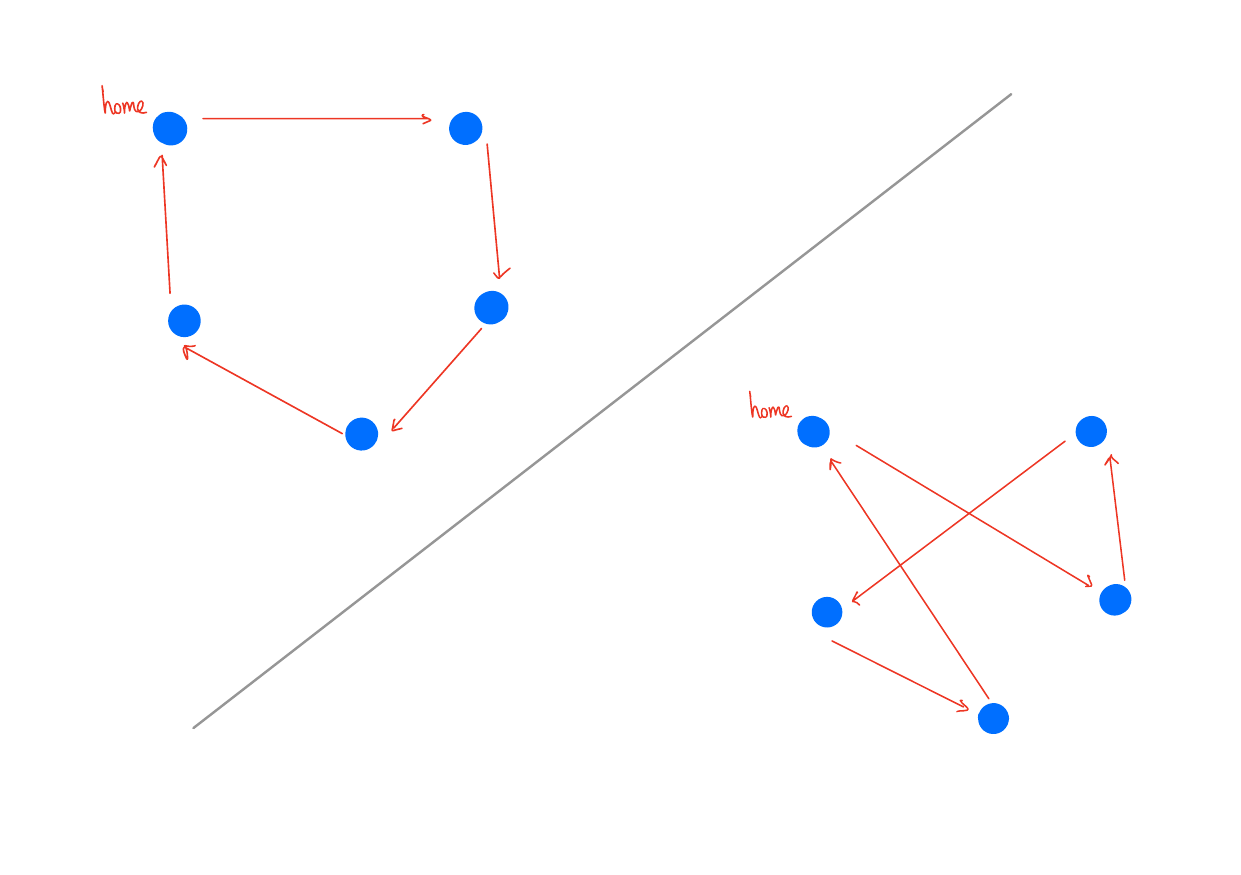
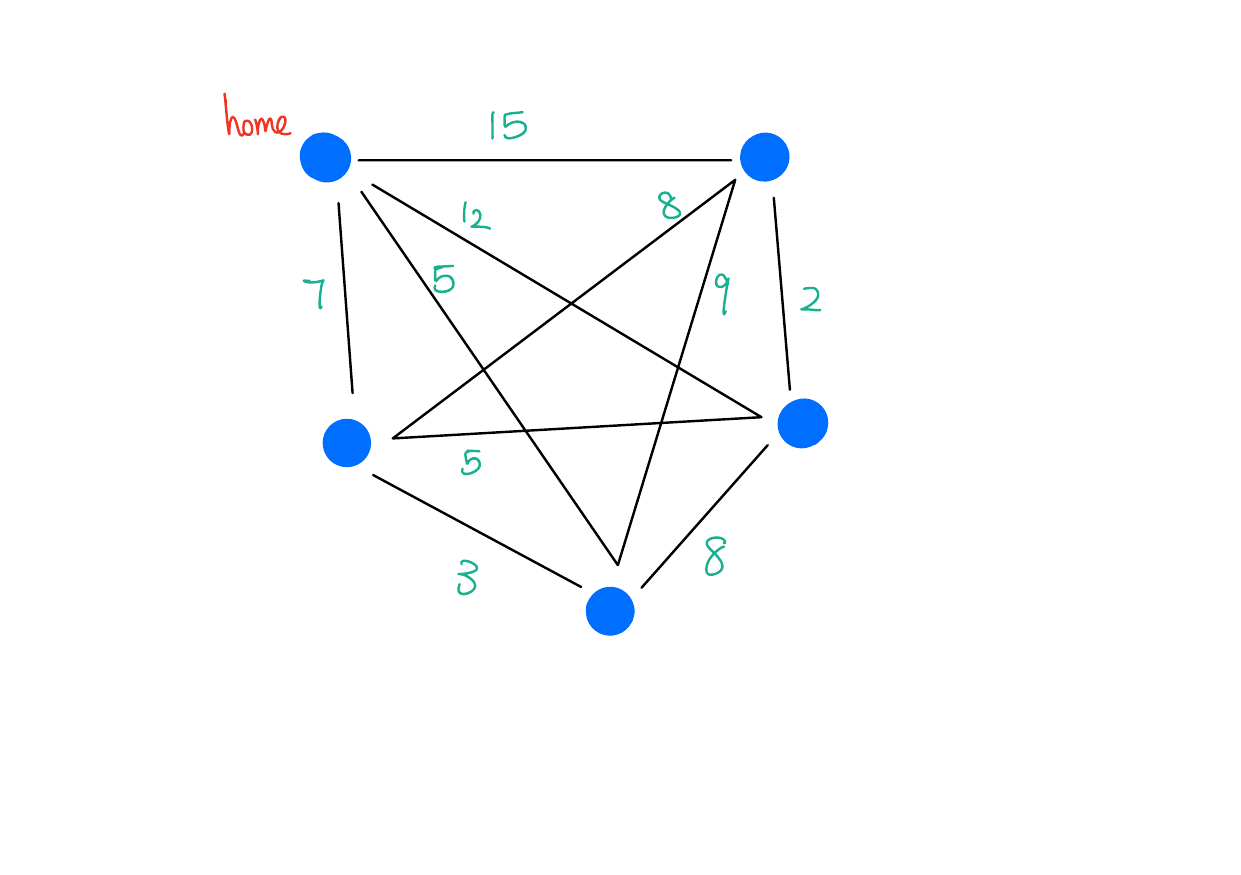
Selling Strawberries

Imagine you’re a door-to-door strawberry salesperson. Let \(H\) be the set of homes in your neighborhood. You live at \(h \in H\).

Selling Strawberries

Trees - A special type of graph

Trees

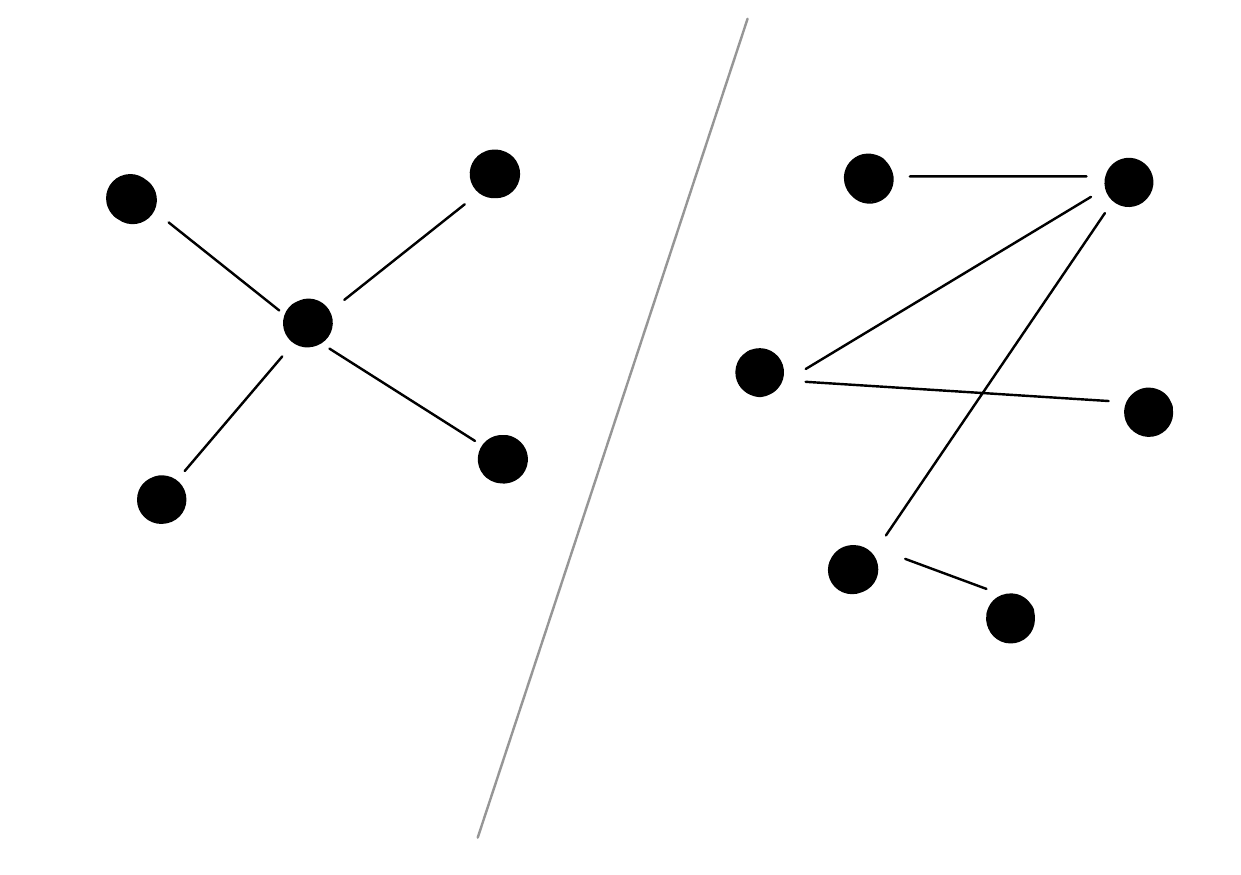
Definition 5 (Connected, Acyclic, Tree) Let \(G = (V, E)\) be any graph.

  • \(G\) is connected if for every pair of distinct vertices \(u, v\), there is some path from \(u\) to \(v\).
  • \(G\) is acyclic if there are no cycles in \(G\).
  • \(G\) is called a tree if \(G\) is both connected and acyclic.

Examples

Trees - on a knife’s edge

If \(G\) has many edges, it’s more likely to be connected, but also more likely to have a cycle.

If \(G\) has fewer edges, it’s more likely to be acyclic but less likely to be connected.

Since trees are both connected and acyclic, trees represent a perfect compromise. However, as we will see on the next slide, any addition or subtraction of an edge will destroy the balance.

Trees - on a knife’s edge

Trees are minimally connected, meaning that it is connected but removing any edge causes the tree to be disconnected.

Trees are maximally acyclic, meaning that there is no cycle, but adding any edge creates a cycle.

Proof: Minimally Connected

Tree: connected and acyclic.

WTS: Removing any edge causes the tree to be disconnected.

Proof

Let \(G = (V, E)\) be a tree. Suppose \(\{u, v\}\) is an edge in \(G\). Let \(G' = (V, E \setminus\{\{u, v\}\})\) be the graph with \(\{u, v\}\) removed. We’ll show that \(G'\) is disconnected - in particular, there is no path from \(u\) to \(v\).

By contradiction, if there was a path \(P = (u = v_1,v_2,...,v_n=v)\) from \(u\) to \(v\) in \(G'\), then the \(C = (u = v_1,v_2,...,v_n=v, u)\) is a cycle in \(G\). However, \(G\) is acyclic, so this is a contradiction.

Proof: Maximally Acyclic

Tree: connected and acyclic.

WTS: Adding any edge creates a cycle

Proof

Let \(G = (V, E)\) be a tree. Suppose \(\{u, v\}\) is an edge not in \(G\). Let \(G' = (V, E \cup\{\{u, v\}\})\) be the graph with the edge \(\{u, v\}\) added. We’ll show that \(G'\) has a cycle.

Since \(G\) is connected, there is some path \(P = (u=v_1,...,v_n = v)\) from \(u\) to \(v\) in \(G\). Then \(C = (u=v_1,...,v_n=v, u)\) is a cycle in \(G'\).

Converses

Let \(G\) be a graph.

  • If \(G\) is minimally connected. Then \(G\) is a tree.

  • If \(G\) is maximally acyclic. Then \(G\) is a tree.

Are these also true? Yes!

How many edges does a tree have?

Solution \(|V|-1\). We will prove this next time.

Problem 4. Minimum Spanning Tree

Electrical Grid

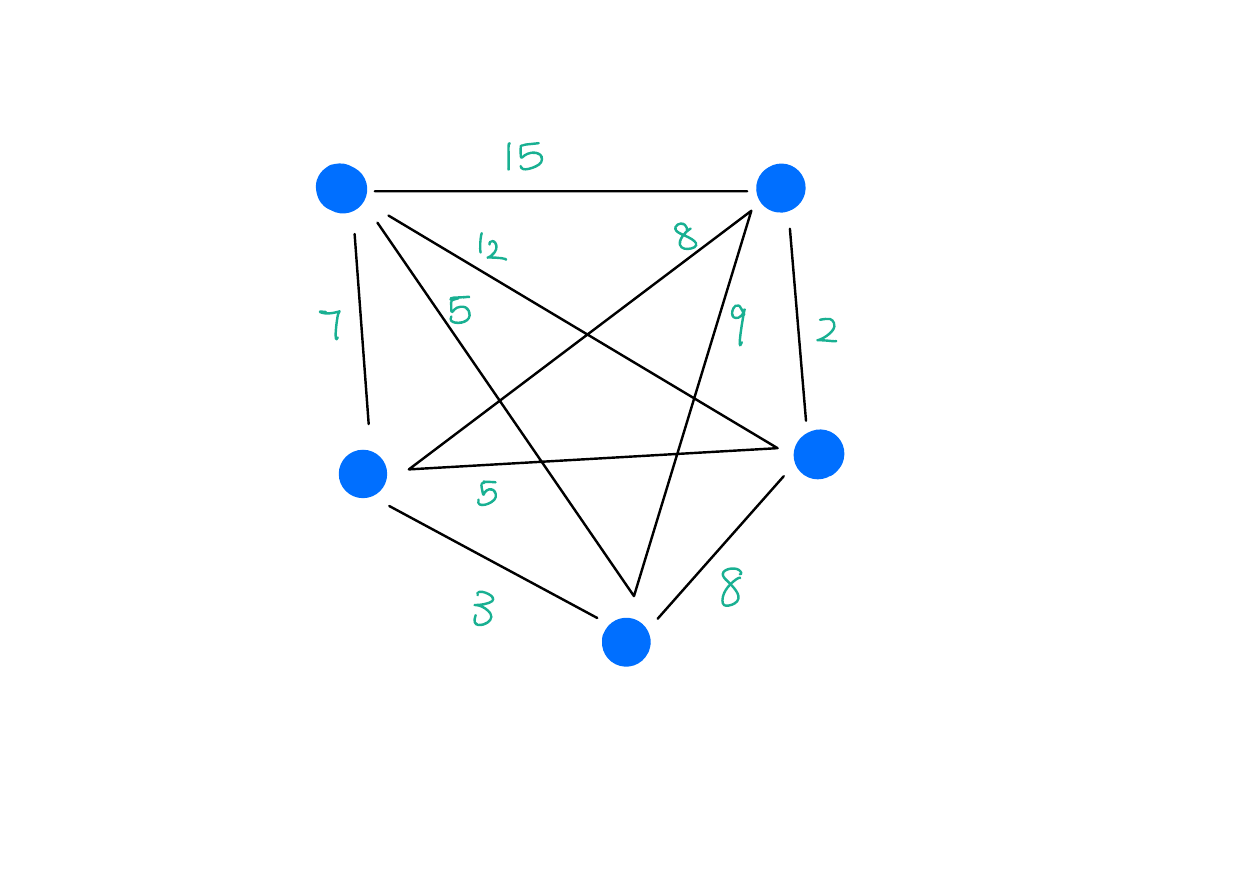
Minimum Spanning Tree

Input: A connected, weighted graph \(G = (V, E)\).

Output: A graph \(T = (V, E')\), where \(E' \subseteq E\), such that \(T\) is a tree that minimizes the total edge weights.

Example

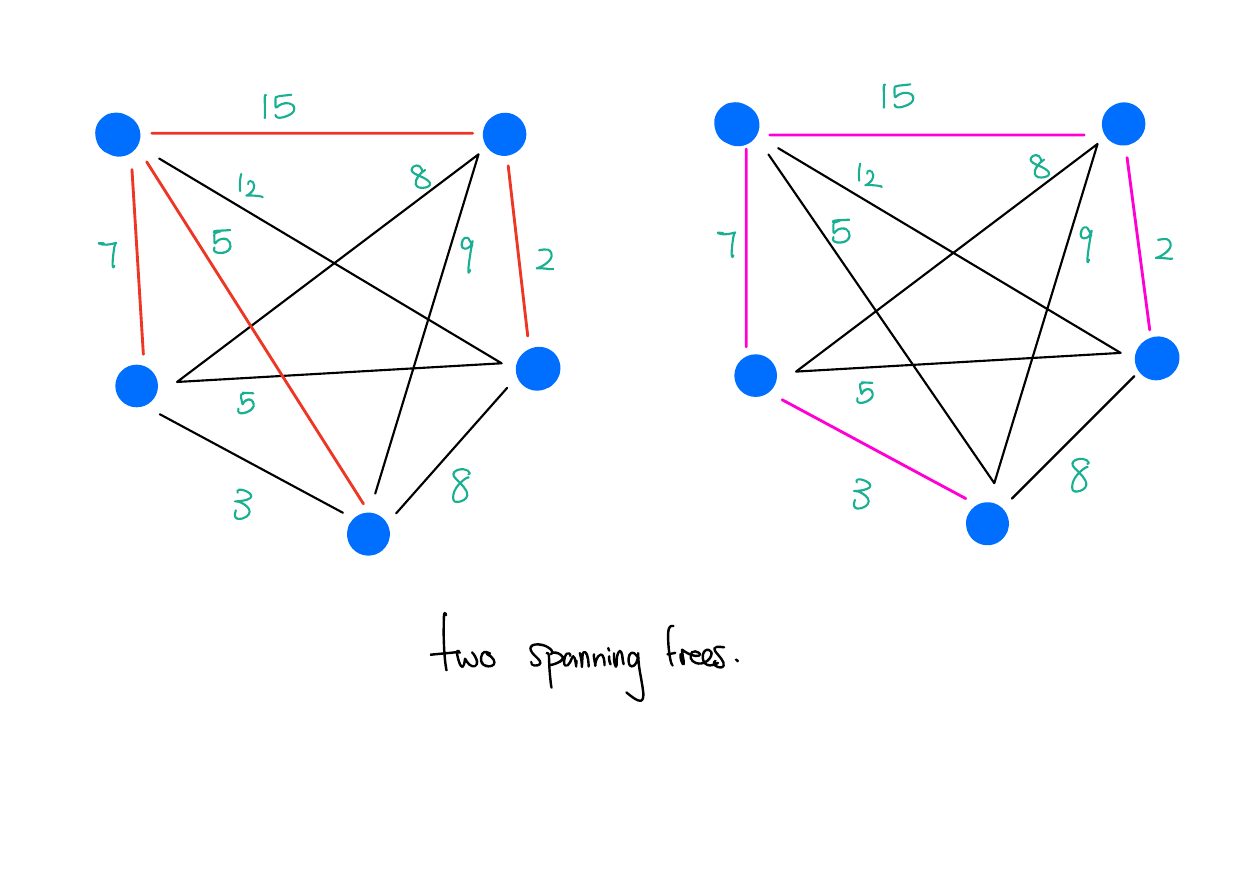
Which of these problems seem more difficult?

  • Minimum Spanning Tree
  • Shortest Path
  • Matching
  • Traveling Salesman
Comment We know fast algorithms for the first three, but NOT for the last one.
In fact, the Traveling Salesman problem is conjectured to have no efficient algorithm. You’ll see more in CSC373.

Additional Notes

  • The skill I want you to develop here is to identify how real-world problems can be translated into known problems on graphs.
  • We did not study in detail HOW to solve such problems (that’s the main topic of CSC373).
  • Even though we don’t know of a good algorithm for TSP, we do have fast approximation algorithms for it.

Here are some references for some algorithms in case you are curious.