Problem Set 1
Functions
1 Inverses
Let \(f: A \to B\) be a function. A function \(g: B \to A\) is
a left inverse of \(f\) if \(\forall a \in A\). \(g(f(a)) = a\).
a right inverse of \(f\) if \(\forall b \in B\). \(f(g(b)) = b\).
a true inverse (usually just called an inverse) of \(f\) if \(g\) is both a right inverse and a left inverse.
1.1
Show that \(f\) is injective if and only if \(f\) has a left inverse.
Solution
Forward direction. Let \(A, B\) be non-empty sets. Assume \(f:A \to B\) is injective. Since \(A\) is non-empty, assume \(\alpha \in A\). We claim \(g:B \to A\) defined by
\[ g(b) = \begin{cases} a & \text{if } f(a) = b \\ \alpha & \text{else} \end{cases} \]
is a left inverse. First we need to show that \(g\) is a valid function. Since \(f\) is injective, the condition that \(f(a) = b\) is satisfied by at most one element \(a \in A\), and thus \(g\) is well defined (i.e. every \(b \in B\) is mapped to some element of \(A\)). To show that \(g\) is a left inverse, consider any \(a \in A\). Since \(f(a) = f(a)\), \(g(f(a))\) always enters the first case and \(g(f(a)) = a\) as required.
Backward direction. Let \(A, B\) be non-empty sets, \(f: A \to B\) be any function. Suppose \(g:B \to A\) is a left inverse of \(f\). We will show that \(f\) is injective.
To that end, Let \(a, b \in A\) be arbitrary elements with \(f(a) = f(b)\). Applying \(g\) to both sides we get
\[ \begin{aligned} g(f(a)) & = g(f(b)) \\ a &= b \end{aligned} \]
where the second line follows since \(g\) is a left inverse. Thus, \(f\) is injective as required.
1.2
Show that if \(f\) has a right inverse, then it is surjective. Note that it is also true (assuming the Axiom of Choice (don’t worry about this)) that if \(f\) is surjective, it has a right inverse.
Solution
Let \(f:A \to B\) be any function and suppose \(g: B \to A\) is a right inverse of \(f\). We will show that \(f\) is surjective.
Let \(b \in B\) be any element. Then we have \(f(g(b)) = b\) since \(g\) is a right inverse of \(f\). Therefore \(f\) is surjective as required.1.3
Assuming the above, show that a function has a true inverse if and only if it is bijective. Your solution for this part of the problem should not exceed four sentences.
Solution
Forward Direction. Assume \(f:A \to B\) has a true inverse \(g: B \to A\). Then since \(g\) is both a left and a right inverse of \(f\), by the previous parts of the problem, \(f\) is both injective and surjective.
Backward Direction. Assume \(f:A \to B\) is bijective. Since \(f\) is injective, \(f\) has a left inverse \(g: B \to A\). We claim that \(g\) is also a right inverse. Let \(b \in B\), since \(f\) is surjective, we have \(b = f(a)\) for some \(a \in A\), and hence
\[f(g(b)) = f(g(f(a))) = f(a) = b,\] where second equality follows because \(f\) is a left inverse of \(g\). Thus \(g\) is a true inverse as required.1.4
Use any of the results from this question (or otherwise) to prove that if there is an injective function \(f: A \to B\), then there is a surjective function \(g:B\to A\).
Solution
Let \(f:A \to B\) be an injective function. Then \(f\) has a left inverse \(g: B \to A\) by part a of the problem. We’ll show that \(g\) is surjective. Since \(g\) is a left inverse of \(f\), for any \(a \in A\), we have \[g(f(a)) = a.\] Thus, \(f\) is the right inverse of \(g\). Since \(g\) has a right inverse, \(g\) is surjective by part 1b.
This problem gives you a new way to prove that a function is injective or surjective or bijective. To show a function is injective you can find a left inverse, to show a function is surjective, you can find a right inverse and to show a function is bijective you can find a true inverse!
2 Hilbert’s Hotel
In the lecture, we saw the example of an infinite hotel where the rooms are numbered using the natural numbers \(\mathbb{N}\).
Let \(C\) be the set of customers. Your job is the define the \(\mathrm{Assigns}: C \to \mathbb{N}\) function that assigns customers to hotel rooms. Since each room only fits one person, we need this function to be injective.
In the lecture, we saw that when a bus containing an infinite (one for each natural number) number of people arrived at the hotel, we could fit them all in. Surprisingly, when a second bus containing an infinite (one for each natural number) number of people, we could still fit everyone in.
In this problem, we will test the limits of the infinite hotel.
2.1
Now, let \(n \in \mathbb{N}\) be some number. Imagine \(n\) busses containing an infinite (one for each natural number) of people show up. For notation, let \(C_n = \{0,1,2...,n-1\} \times \mathbb{N}\) be the set of customers, where \((i, j) \in C_n\) refers to the \(j\)th person on the \(i\)th bus. Prove that you can fit everyone in the hotel for any number of busses \(n\). I.e. find an injective function \(\mathrm{Assigns}:C_n \to \mathbb{N}\) for any \(n\). Prove that your function is injective.
Solution
This is a generalization of the two bus example from lecture. Let \(n \in \mathbb{N}\) be any natural numbers greater than \(0\). We claim \(f_n: C_n \to \mathbb{N}\) defined by \(f_n(i, j) = j\cdot n + i\) is injective. Intuitively, bus \(i\) gets all the rooms with remainder \(i\) when divided by \(n\).
Suppose \(f_n(i, j) = f_n(x, y)\), then we have \[ jn + i = yn + x. \] Since \(i, x < n\), it must be the case that \(y = j\). Taking both sides mod \(n\), we also get \(i = x\). Therefore, \((i,j) = (x, y)\) and \(f_n\) is injective as required.2.2
Now imagine an infinite number (one for each natural number) of busses containing an infinite (one for each natural) number of people show up. For notation, let \(C_{\infty} = \mathbb{N}\times \mathbb{N}\) be the set of customers, where again customer \((i, j) \in C_\infty\) refers to the \(j\)th person on the \(i\)th bus. Prove that you can still fit everyone in the hotel. I.e. find an injective function \(\mathrm{Assigns}: C_\infty \to \mathbb{N}\). Prove that your function is injective.
Solution
We need to find an injective function \(f: \mathbb{N}\times \mathbb{N}\to \mathbb{N}\). There are several ways to do this, here is one example, for any \(i, j \in \mathbb{N}\), let \(f(i, j) = 2^i3^j.\)
Assume \(f(i, j) = f(x, y)\). Then we have \(2^i3^j = 2^x3^y\). Since two numbers are equal if and only if they have the same factors, and \(2\) and \(3\) are prime, \(i = x\) and \(j=y\), and hence \((i,j) = (x,y)\) and \(f\) is injective as required.3 Friends and Strangers
Suppose you’re at a social event with six people. Every pair of people are either friends or strangers.
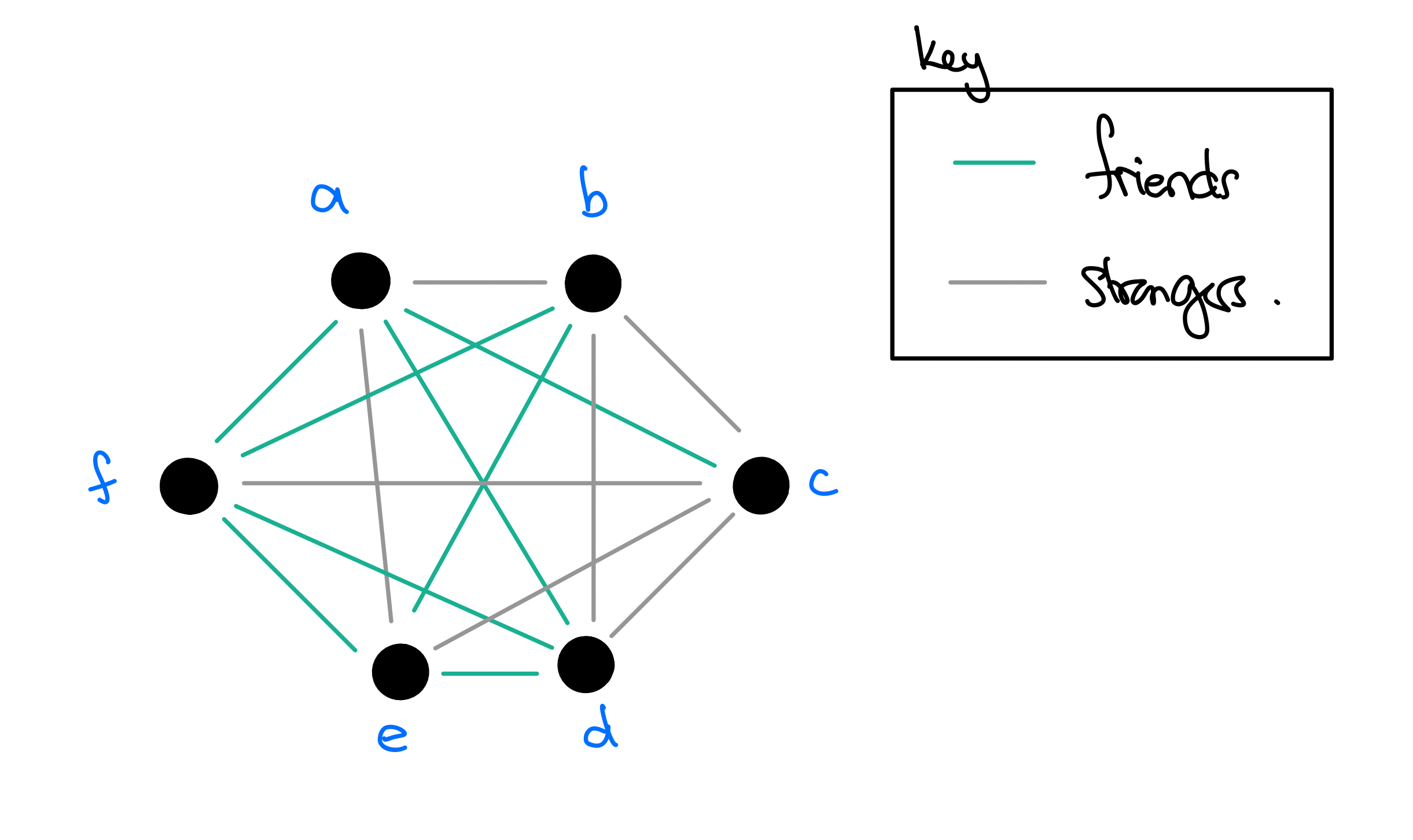
3.1
Take any person \(p\). Show that \(p\) is either friends with at least three people or strangers with at least three people.
Solution
Also see Logan’s walkthrough video.
Let \(p\) be any of the six people. Each of the other five people falls into one of two categories: friends or strangers of \(p\). Applying the generalized pigeonhole principle, we have that at least one category must have at least \(\lceil 5/2 \rceil = 3\) people. In other words, \(p\) is either friends with at least three people or strangers with at least three people.
3.2
Show that for any configuration of friendships/strangerships there must be a group of three mutual friends or three mutual strangers. For example, in the picture, \(d, e\) and \(f\) are mutual friends and \(b, c, d\) are mutual strangers.
More precisely, show that there exist three distinct people \(a, b, c\) in the party such that either
\(a\) is friends with \(b\), \(b\) is friends with \(c\), and \(c\) is friends with \(a\).
OR
\(a\) and \(b\) are strangers, \(b\) and \(c\) are strangers, and \(c\) and \(a\) are strangers.
Solution
Let \(p\) be any person. From part \(a\), we know that \(p\) is either friends with at least three people or strangers with at least three people. WLOG, assume \(p\) is friends with at least three people, and let \(F\) be the set of \(p\)’s friends with \(|F| \geq 3\).
There are 2 cases
If \(F\) is a set of mutual strangers, since \(|F|\geq 3\), we have found a set of three mutual strangers.
Otherwise, there exists \(a, b \in F\) such that \(a\) and \(b\) are friends. Then \(a, b, p\) form a mutual friendship.
Thus, there is a group of three mutual friends or three mutual strangers.
3.3
Now, imagine the following similar scenario.
Let \(S\) be a set of \(k\) people such that \(\forall u, v \in S\) with \(u \neq v\), \(u\) and \(v\) are either friends, strangers, or enemies. Note that these relationships are bidirectional.
Find \(k \in \mathbb{N}\) such that any set of \(k\) people have a group of 3 mutual strangers, 3 mutual friends or 3 mutual enemies.
Solution
Any \(k \geq 17\) works. Let \(S\) be a set of \(17\) people. Let \(x \in S\) be any person. There are 16 other people, each of which can be one of three labels. By the Generalized Pigeonhole Principle, one of the three labels has at least \(\left\lceil 16/3 \right\rceil = 6\) people. WLOG, assume \(x\) has at least \(6\) enemies, and let \(E\) be a set of \(6\) of these enemies.
If any two people, \(a, b \in E\) are enemies, then \(x, a, b\) are three mutual enemies.
Otherwise, for every pair \(a, b \in E\), \(a\) and \(b\) are friends or strangers. By HW1, since \(|E| = 6\), \(E\) contains either three mutual friends or three mutual strangers.
In any case, there is a group of three mutual friends, three mutual strangers, or three mutual enemies.
4 Functional Programming
This the coding part of this problem optional but recommended. If you don’t wish to code, at least familiarize youself with the concepts of function compoisition and partial application.
Functional programming is a paradigm for writing code that contrasts with object-oriented programming. As the name suggests, functional programming is all about functions. In recent years, functional programming has become more popular for its scalability, security, and predictability. In this question, we’ll explore some concepts from functional programming.
Suppose we’re trying to train a machine learning algorithm to classify between two types of apples labeled \(0\) or \(1\) (think Fuji and Honeycrisp). Our data is given to us in CSV (Comma Seperated Value) format in one long string, which looks like this:

Note \n is the ‘newline’ character. For this data to be actually useful, we need to parse it into the following format:

Note that this is a list of list of integers. Each column corresponds to a single feature: label, crunch, sweetness, sourness, mass, and volume, and each row corresponds to a single apple.
We have two function split and str2int available to use. See here. You can click ‘Execute’ to see the output.
A note about the programming language (Haskell): Where most programming languages use f(a, b, c) to call the function f on inputs a, b, c, in Haskell, you’d write f a b c. That is, parentheses are not required, and spaces are used instead of commas to separate inputs.
4.1
Denote by \(\mathrm{Int}\), \(\mathrm{String}\), \(\mathrm{Char}\) the set of integers, strings and characters respectively.
For any set \(A\), let \(\mathrm{List}[A]\) be the set of lists that contain elements from \(A\).
\(\mathrm{split}: \mathrm{Char} \times \mathrm{String} \to \mathrm{List[String]}\)
\(\mathrm{str2int}: \mathrm{String} \to \mathrm{Int}\)
Note that for str2int, there are some caveats when the string does not encode a valid integer. We’ll give full credit to the above solution OR any solution that handles this additional case.
What is the domain and codomain of split? How about str2int?
4.2 (Optional)
For functions that take in multiple inputs, use product notation. For example, the domain for the function ‘concat(a,b)’ which returns the concatenation of the strings a and b has domain \(\mathrm{String} \times \mathrm{String}\), and codomain \(\mathrm{String}\).
map is a special function that takes two inputs. The first input is a function \(f:A \to B\) (yes, functions can be inputs to other functions!) The second is a list of elements from \(A\). map then applies \(f\) to every element of the list. I.e.
map(f, [x1,x2,x3,...]) = [f(x1), f(x2), f(x3),...]
Informally, think of map as being a function from \(\mathrm{Funs}[A, B] \times \mathrm{List}[A] \to \mathrm{List}[B]\). Where \(\mathrm{Funs}[A,B]\) is the set of all functions from \(A\) to \(B\). See it in action using the same link as before.
Here are two more definitions:
For any function \(f: A \times B \to C\), and \(a \in A\), let \(f(a, \cdot): B \to C\) denote the function that maps \(b \in B\) to \(f(a, b)\). I.e. \(f(a, \cdot)\) fixes the first parameter of \(f\) to be \(a\). This process is called partial application. In Haskell, to partially apply a function, simply call it on fewer than expected parameters! i.e. the function \(f(a, \cdot)\) is f a in Haskell.
For any functions \(f: A \to B\), \(g: B \to C\), define their composition \(g\circ f:A \to C\) to be the function that first applies \(f\) and then applies \(g\). I.e. \(g\circ f(a) = g(f(a))\). In Haskell, to compose two functions g and f write g . f
Using split, map, str2int, partial applications of those functions, and composition, define a function \(\mathrm{prep}\) that parses a CSV string. It should take rawData to the list of list of integers shown above.
Note that you must write your function as a composition of other functions. I.e. define \(f = g \circ h\) for some functions \(g, h\), instead of writing \(f(a) = ...\). You can (and may find it helpful to) define intermediate/helper functions but these should also be compositions of other functions.
It is recommended that you write your solution in Haskell (fork the jdoodle) since that way you’ll be able to test it!
For context, there is a solution in at most 80 characters and 16 words.
Hint: keep track of the domains and codomains!
Solution
Here’s one way to do it
prepRow takes in a string corresponding to one row and returns the list of integers that row contains.
prep splits on \n to get a list of strings representing rows, and then applies prepRow to each of these strings.