Problem Set 3

Induction

1 Induction

1.1

Show that for all $n \in \mathbb{N}$ with $n \geq 1$, \[\left(1 + \frac{1}{1}\right) \left(1 + \frac{1}{2}\right) \left(1 + \frac{1}{3}\right) ... \left(1 + \frac{1}{n}\right) = n + 1\]

Solution

Let $P(n)$ be the predicate \[\left(1 + \frac{1}{1}\right) ... \left(1 + \frac{1}{n}\right) = n + 1\] By induction.

Base case. For $n = 1$, we have $(1 + 1/1) = 1 + 1$. Thus, the base case holds. Inductive step. Let $k \in \mathbb{N}$ be any natural number with $k \geq 1$, and assume $P(k)$. We’ll show $P(k+1)$.

$$ \[\begin{aligned} \left(1 + \frac{1}{1}\right) ... \left(1 + \frac{1}{k}\right) \left(1 + \frac{1}{k+1}\right) & = (k+1)\left(1 + \frac{1}{k+1}\right) \\ & = (k+1) + \frac{k+1}{k+1} \\ & = (k+1) + 1, \end{aligned}\]

where the first equality holds by the induction hypothesis, as required.

1.2

Show by induction $\forall n \in \mathbb{N}. (n^3 \leq 3^n)$.

Solution

We first note that the claim holds for $n = 0, 1, 2$ since $0^3 = 0 \leq 3^0$, $1^3 = 1 \leq 3^1$, and $2^3 = 8 \leq 3^2 = 9$.

We will now show that $\forall n \in \mathbb{N}, n\geq 3. (n^3 \leq 3^n)$. By induction.

Base case. For $n = 3$, both the LHS and the RHS of the equation are $3^3$ and thus equal. Inductive step. Let $k \in \mathbb{N}$, with $k \geq 3$ be any natural number at least 3. Suppose $k^3 \leq 3^k$. Then we have the following

$$ \[\begin{aligned} (k+1)^3 & = k^3 + 3k^2 + 3k + 1 \\ & \leq k^3 + k^3 + k^2 + k & (k \geq 3) \\ & \leq k^3 + k^3 + k^2 + k^2 & (k^2 \geq k) \\ & \leq k^3 + k^3 + 3k^2 & (3k^2 \geq 2k^2) \\ & \leq k^3 + k^3 + k^3 & (k \geq 3) \\ & = 3k^3 \\ & \leq 3\cdot 3^k & (\text{IH}) \\ & = 3^{k+1} \end{aligned}\]

$$ which completes the induction.

1.3

Your friend claims the following. Claim: $a^n = 1$ for all $n \in \mathbb{N}, a \in \mathbb{R}_{>0}$, and proposes the following proof by complete induction.

Proof. Base case. The base case holds since $a^0 = 1$ for any non-zero $a$.

Inductive step. Let $k \in \mathbb{N}$ be any natural number and assume for every $m \leq k$, and $a \in \mathbb{R}_{>0}$, $a^m = 1$. Then we have

\[a^{k+1} = a^{k + k - (k - 1)} = \frac{a^k\cdot a^k}{a^{k-1}} = \frac{1 \cdot 1}{1} = 1,\]

which completes the induction. ◻

Find the flaw in the following argument, and explain the mistake.

Solution

You can’t use $a^{k-1}$ in the inductive step since when $k = 0$, $k-1$ is not a natural number and hence is not included in the inductive hypothesis.

1.4

Define the function $f: \mathbb{N}_{\geq 1} \to \mathbb{N}$ recursively as follows \[ \begin{aligned} f(n) = \begin{cases} 0 & n=1 \\ 3 & n=2 \\ 2f(n-1) - f(n-2) + 2 & n\geq2 \\ \end{cases} \end{aligned} \] Show $\forall n \in \mathbb{N}, n \geq 1, f(n) \leq n^2$.

Your friend proposes the following (incorrect) proof.

Let $P(n)$ be the predicate that is true when $f(n) \leq n^2$. By complete induction.

Base case. We’ll show $P(1)$, $P(2)$. For $n=1$, $1^2 = 1$, and $f(1) = 0$, and $0 \leq 1$. For $n=2$, $2^2 = 4$, and $f(2) = 3$, and $3 \leq 4$. Thus, the base cases hold.

Inductive step. Let $k \in \mathbb{N}$ with $k \geq 2$, and suppose for the inductive hypothesis that for all $i \in \mathbb{N}$ with $1 \leq i \leq k$, $P(i)$ . We’ll show $P(k+1)$. \[ \begin{aligned} f(k+1) & = 2f(k) - f(k-1) + 2 \\ & \leq 2k^2 - (k-1)^2 + 2 & (\text{IH}) \\ & = 2k^2 - (k^2 -2k + 1) + 2 \\ & = k^2 +2k - 1 + 2 \\ & = k^2 +2k + 1 \\ & = (k+1)^2 \end{aligned} \] This completes the induction.

Point out the invalid step in the proof and explain why it is invalid.

Solution

The first inequality is incorrect. To get the $\leq$, we are allowed to replace the RHS with something larger. The inductive hypothesis applied to $k-1$ says that $f(k-1) \leq (k-1)^2$, which implies $-f(k+1) \geq -(k-1)^2$, so we are not justified in replacing $-f(k+1)$ with $-(k-1)^2$.

1.5

Although the above proof is invalid, the result is still true. I.e., it is true that $\forall n \in \mathbb{N}, n \geq 1. f(n) \leq n^2$.

Prove $\forall n \in \mathbb{N}, n \geq 1. f(n) \leq n^2$.

Solution

We’ll show $\forall n \in \mathbb{N}, n \geq 1. f(n) = n^2 - 1$. Since for any $n \in \mathbb{N}$, $n^2 - 1 \leq n^2$ this is clearly sufficient.

By (complete) induction.

Base case. For the base case, $f(1) = 0 = 1^2 - 1$, and $f(2) = 3 = 2^2 - 1$. Thus, the base case holds.

Inductive step. Let $k \in \mathbb{N}$ with $k \geq 2$, and assume for all $i \in \mathbb{N}$ with $1 \leq i \leq k$, $f(i) = i^2 -1$, we’ll show $f(k+1) = (k+1)^2 -1$

$$ \[\begin{align*} f(k+1) & =2f(k) - f(k-1) + 2 \\ & = 2(k^2 - 1) - ((k-1)^2 - 1) + 2 & \text{(IH)} \\ & = 2k^2 - 2 - ((k^2 - 2k +1) - 1) + 2 \\ & = 2k^2 - (k^2 - 2k) \\ & = k^2 + 2k \\ & = k^2 + 2k + 1 - 1 \\ & = (k+1)^2 - 1 \end{align*}\] $$

2 Task Scheduling

Suppose you had a bunch of tasks. Here’s a small example:

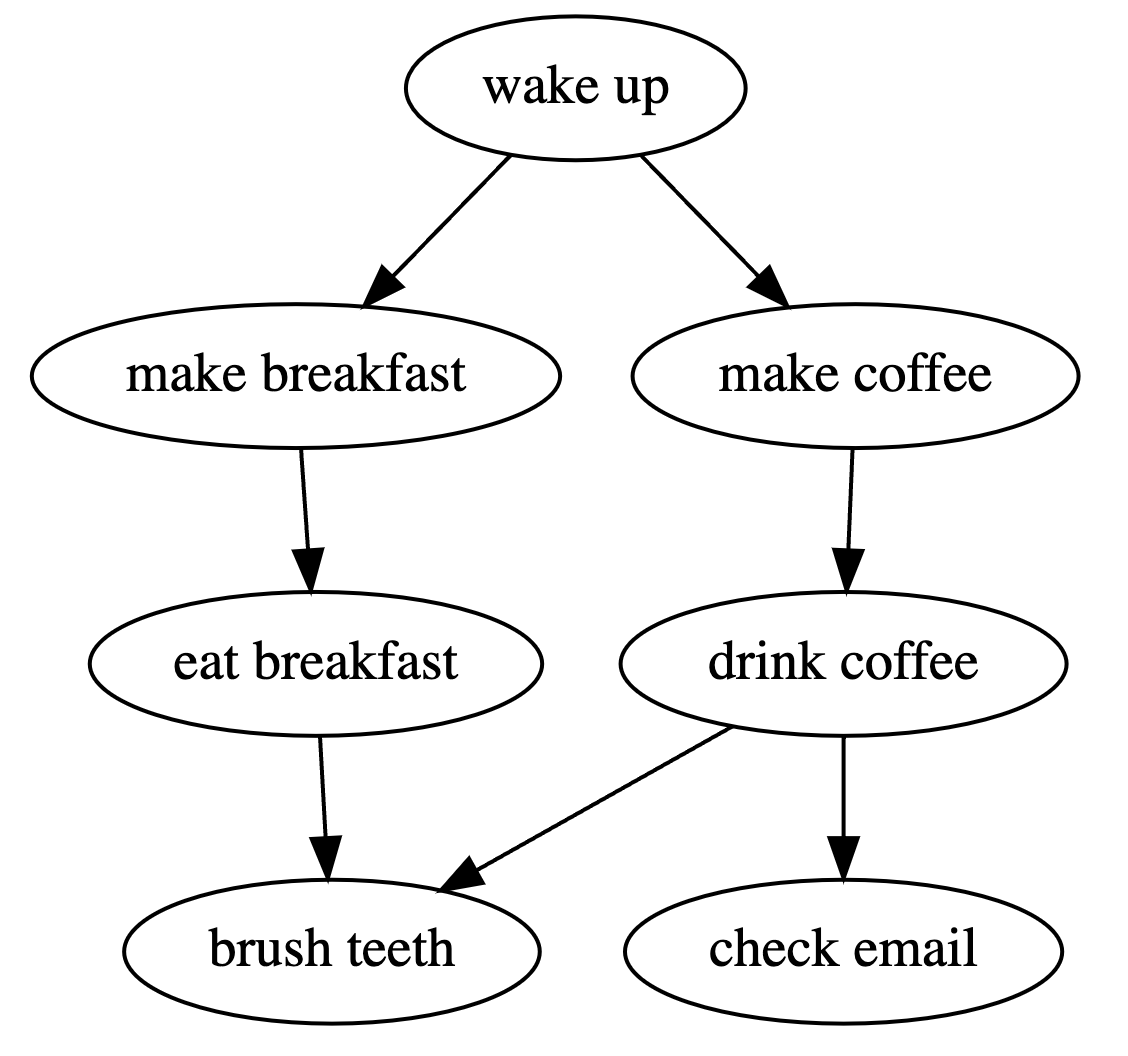
In this problem, we’ll study the problem of finding a valid ordering of the tasks.

Call task $a$ a prerequisite for task $b$ if task $a$ must be done before $b$, and write $a \prec b$.

Let $T$ be a set of $n$ tasks. Let $t_1,...,t_n$ be an ordering of the elements in $T$. We say that the ordering respects $\prec$ if there does not exist $i, j \in [n]$ such that $i < j$ and $t_j \prec t_i$. In other words, if $t_j$ appears after $t_i$, $t_j$ is not a prerequisite for $t_i$.

2.1

Give two orderings that respect the morning schedule example (in that example, $a\prec b$ if there is a directed edge from $a$ to $b$).

Solution

Wake up, make breakfast, make coffee, eat breakfast, drink coffee, brush teeth, check email
Wake up, make coffee, drink coffee, check email, make breakfast, eat breakfast, brush teeth

2.2

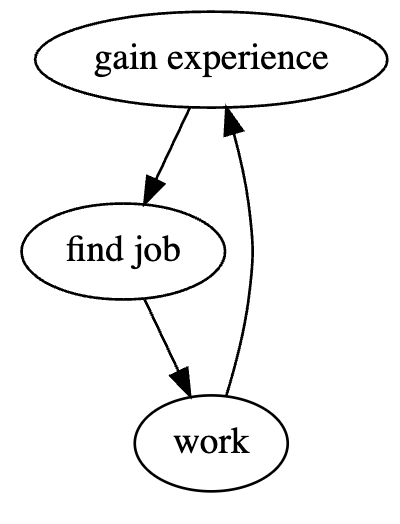
Argue that there is no valid ordering for the following example.

Solution

Since each task has a prerequisite, none of them can be the first task.

2.3

Let’s impose some additional constraints on what kind of relationships we can allow. In particular, call $\prec$ valid a valid prerequisite relation over $T$ if it satisfies the following.

$\forall a, b, c \in T$.

$a\not\prec a$. That is, no task is a prerequisite of itself.
If $a \prec b$, and $b \prec c$, then $a\prec c$. That is, a prerequisite of a prerequisite is also a prerequisite.

Call a task $a \in T$ minimal if it does not have any prerequisites.

Show that $\forall n\geq 1$, if $T$ is a set of $n$ tasks and $\prec$ is a valid prerequisite relation over $T$, then $T$ has a minimal element.

Solution

Let $P(n)$ be the following predicate: For every set $T$ on $n$ elements and every valid prerequisites relation over $T$, $T$ has a minimal element.

By induction.

Base case. For $n = 1$, $T$ contains a single element $a$, since no task is a prerequisite of itself, $a$ has no prerequisites.

Inductive step. Let $k \in \mathbb{N}$ with $k \geq 1$, and assume $P(k)$. Now let $T$ be a set of $k+1$ elements and $\prec$ be a valid prerequisite relation over $T$. Let $a$ be any element in $T$, and consider the set $T'$. Note that $T'$ is a set of $k$ elements, and note that $\prec$ is still a valid prerequisite relation over $T'$. Thus, by the inductive hypothesis, $T'$ has a minimal element $b$.

If $a \not \prec b$, then $b$ is still minimal in $T$, and we’re done. Otherwise, $a \prec b$. In this case, we claim that $a$ is minimal in $T$. By contradiction, assume $a$ was not minimal. Then there is some $c \in T$ such that $c \prec a$. Since $c \prec a$, and $a \prec b$, we have $c \prec b$, which contradicts the minimality of $b$ in $T'$.

2.4

Show that for any finite, non-empty set of tasks $T$, and valid prerequisite structure $\prec$ on $T$, there is a valid ordering of the tasks in $T$.

Solution

We’ll show that $\forall n \in \mathbb{N}$ with $n \geq 1$, if $T$ is a set of size $n$, and $\prec$ is a valid prerequisite relation over $T$, then there exists a valid ordering. By induction.

Base case. Let $T$ be a set of size $1$. $T$ contains a single element $a$ and this is already an ordering that respects $\prec$.

Inductive step. Let $k \in \mathbb{N}$ with $k \geq 1$, and assume the claim holds for sets of size $k$. Let $T$ be a set of size $k + 1$. By part 4c, $T$ has a minimal element $a$. Let $T' = T \setminus \{a\}$. By the inductive hypothesis, $T'$ has a ordering ($t_1,...,t_k)$ that respects $\prec$. We claim that $(a, t_1,...,t_k)$ is an ordering of elements of $T$ that respects $\prec$. Since $(t_1,...,t_k)$ was a valid ordering of $T'$, we just need to check that $a$ does not have a prerequisite among $t_1,...,t_k$. This is guaranteed by the fact that $a$ is minimal in $T$.

3 A Neural Network Breakthrough?

Your friend approaches you with a new idea, claiming it is possibly a breakthrough in neural networks for binary classification.

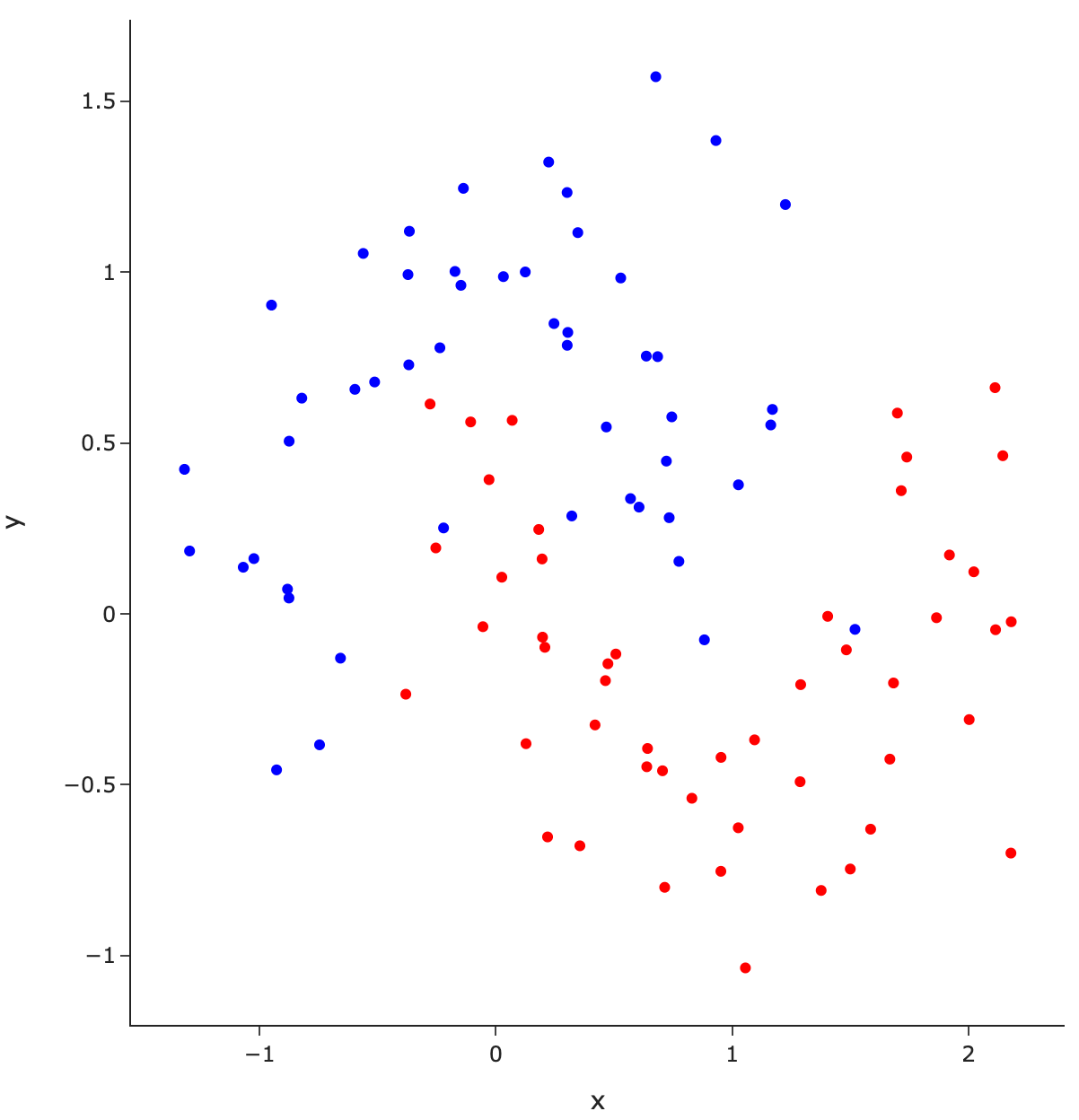
Binary classification is the problem where you’re given some input and asked to classify the input as one of two classes. One example of binary classification is predicting whether a patient has pneumonia based on X-ray images. In this problem, we will focus on predicting whether a point is blue or red given the $x$ and $y$ coordinates.

Our data looks like this:

A neural network is depicted as follows.

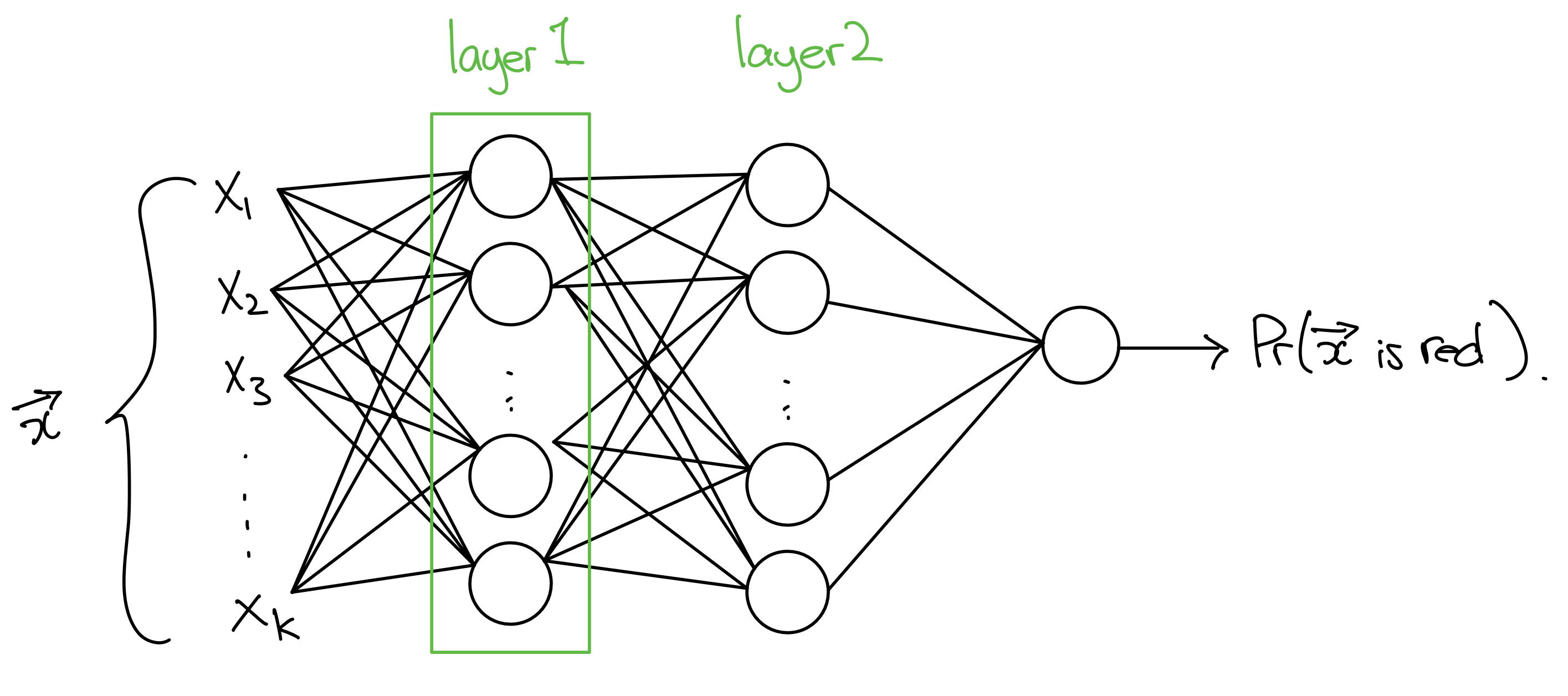
The circles are called neurons. Zooming in on a single neuron:

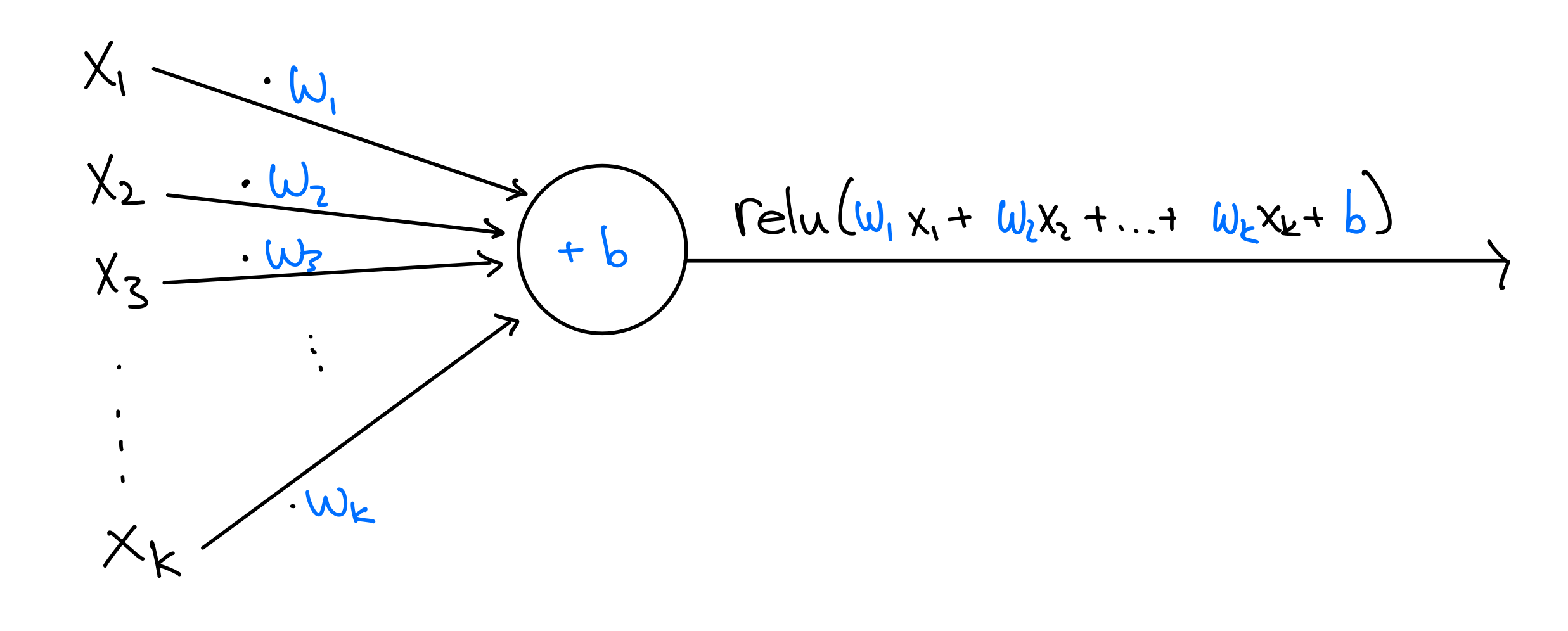
Let $k$ be the number of inputs for a particular neuron. Each neuron stores $k+1$ parameters, one weight, $w_i \in \mathbb{R}$, for each input, and one additional parameter called the bias, $b \in \mathbb{R}$. The output of the neuron is $\mathrm{relu}(w_1x_1 + w_2x_2 + ... + w_kx_k + b)$. In words, the neuron computes the weighted sum of the inputs, adds the bias term, and applies $\mathrm{relu}$. $\mathrm{relu}: \mathbb{R}\to \mathbb{R}$ is function defined as follows

\[ \mathrm{relu}(x) = \begin{cases} 0 & x \leq 0 \\ x & x > 0 \end{cases} \]

Neurons are then arranged into layers so that the first layer receives inputs from the actual inputs, and subsequent layers receive their inputs from the outputs of the previous layers. One reason neural networks are so powerful is that you can have many layers, each transforming the data in more complex ways. The size of a layer is the number of neurons in it.

The final layer contains a single neuron whose output is the probability that the input is red. Then, if the probability is $\geq 0.5$, we predict the point is red; otherwise, it is blue.

The final neuron is very slightly different from the other neurons. It still computes a weighted average of its inputs plus a bias. However, it applies a different function called $\sigma$ (‘sigmoid’) instead of relu.

Here is your friend’s idea:

“Look carefully at what $\mathrm{relu}$ does. If the input to relu is positive, we report the value, but if it is negative, relu just outputs 0. Isn’t that wasting a lot of information? Shouldn’t it be useful for later neurons to know how negative the input was? So here is my idea, instead of having a neuron output $\mathrm{relu}(w_1x_1 + w_2x_2 + ... + w_kx_k + b)$, have it output $w_1x_1 + w_2x_2 + ... + w_kx_k + b$!”

3.1

Test this theory out for yourself here.

First, run the model as is to check that it works.

Then, to test your friend’s theory, remove the activation="relu" optional arguments in the definition of the model and try rerunning it. Try again with more and bigger layers.

How does the model do? Does your friend’s idea work?

3.2

Unfortunately, your friend’s idea doesn’t work. Prove the following statement to show this:

If neurons compute in the suggested way, then any neural network with an arbitrary number of layers with arbitrary sizes is equivalent to some single output neuron (and thus, can’t be all that powerful).

Note

This problem is challenging. Try to think of how you would set up the statement you’re trying to prove as $\forall n. P(n)$, and use induction. Some basic facts about matrix multiplication will be useful.

Solution

First, we’ll make an important observation. Suppose you have a layer that takes $k_{in}$ inputs and has an output size of $k_{out}$. Let $\vec{x}$ be the input to this layer. Then, if you write \[W = \begin{bmatrix} \rule[.5ex]{2.5ex}{0.5pt}\vec{w}_1\rule[.5ex]{2.5ex}{0.5pt}\\ \rule[.5ex]{2.5ex}{0.5pt}\vec{w}_2\rule[.5ex]{2.5ex}{0.5pt}\\ \vdots \\ \rule[.5ex]{2.5ex}{0.5pt}\vec{w}_{k_{out}}\rule[.5ex]{2.5ex}{0.5pt} \end{bmatrix}, \vec{b} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{k_{out}} \end{bmatrix}, \]

where $\vec{w}_i$ and $b_i$ are the weights and the biases of the $i$th neuron in the layer, the output of the layer is $W\vec{x} + \vec{b}$.

We’ll now show the following holds.

$\forall l \in \mathbb{N}$, any neural network with $l$ layers (not including the output or input layers) is equivalent to some 0-layer neural network (which is just a single output neuron).

By induction on $l$.

Base case. The base case is true since a 0-layer neural network is equivalent to itself, which is a 0-layer neural network.

Inductive step. Let $l \in \mathbb{N}$ Suppose the claim is true for $l$-layer neural networks. We’ll show that it is also true for $l+1$ layer neural networks. Consider an arbitrary $l+1$ layer neural network $N$, and look separately at the first layer and the last $l$ layers.

The last $l$ layers is a neural network with $l$ layers. By the inductive hypothesis, it is equivalent to a single output neuron. Let $\vec{w_2}$ and $b_2$ be the weight vector and bias of this equivalent output neuron.

Let $W$ and $\vec{b}$ be the weights and biases of the first layer.

Then, on input $x$, $N$ outputs $\sigma(\vec{w_2}^T(Wx + \vec{b}) + b_2)$. Using facts about matrix multiplication (namely distributivity, and associativity), this is equal to $\sigma((\vec{w_2}^TW)x + (\vec{w_2}^T \vec{b} + b_2))$, and this is computed by a single output neuron with weight vector $\vec{w_2}^TW$, and bias $\vec{w_2}^T \vec{b} + b_2$. This completes the induction.