Problem Set 11

Regular Languages

Note. Some of these problems are from past exams.

1 Automata and Code

A C-style comment looks like this /*``some text here``*/. Let $A$ be the set of C style comments. Let $\Sigma = \{ /, *, a\}$, where we view $a$ as any character that is not $/$ or $*$.

Here are some strings in $A$

/*aaaa*/
/*a*/
/*a//*/
/*a//*a*/
/***/
/**/
/*/*/*/

Here are some strings not in $A$

//aa*/
/aa/
/**/a
/**
$\epsilon$
/*/

Show $A$ is regular by finding either a DFA or an NFA $M$ such that $L(M) = A$.

Solution

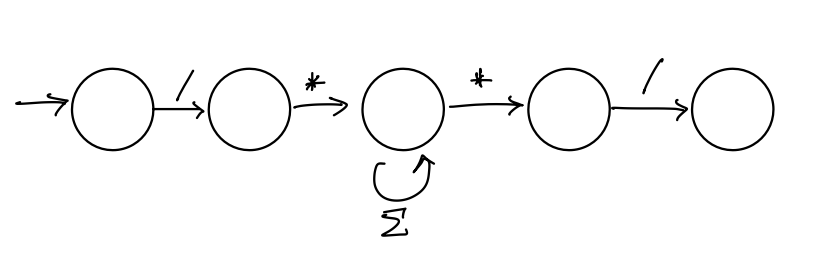
Let $B = \{w \in \{\texttt{(}, \texttt{)}\}^* : \text{every \texttt{(} has a matching \texttt{)}}\}$

Here are some strings in $B$

()
(())()
((())())

Here are some strings not in $B$

(()
)(
()(()

Show that $B$ is not regular.

Solution

Note that from the lecture, it suffices to demonstrate an infinite set of pairwise distinguishable strings.

Let $S = \{(^n: n \in \mathbb{N}\}$. Note that $S$ is infinite (no need to explain.)

Let $x, y \in S$ with $x \neq y$. Then $x = (^i, y = (^j$ for some $i \neq j$. Then since $(^i)^i \in B$ and $(^j)^i \notin B$, $)^i$ distinguishes $x$ and $y$. Thus, $S$ is an infinite set of pairwise distinguishable strings.

2 Regular?

For each of the following languages, determine whether or not the language is regular and prove your answer using any means. If you decide to construct NFAs, DFas, or regular expressions, you do not need to justify their correctness.

Please mark clearly where you start the solution for each subproblem.

$\Sigma = \left\{0,1\right\}$. \[A_{1} = \{w: w \text{ either contains 101 as a substring or has even length, but not both} \}\]
$\Sigma = \{\texttt{a,b,c}\}$. Let $n_a(w), n_b(w), n_c(w)$ be the number of $\texttt{a, b, c}$ in $w$ respectively. \[A_{2} = \{w: n_a(w) + n_b(w) = n_c(w)\mod 3\},\]
$\Sigma = \left\{0,1\right\}$. \[A_{3} = \{w: w \text{ has an equal number of 1s and 0s and length at most 100}\}\]
$\Sigma = \left\{0,1\right\}$. \[A_{4} = \{w: w \text{ has an equal number of 1s and 0s and length a multiple of 3}\}\]
$\Sigma = \left\{0,1\right\}$. \[A_{5} = \{w: |w| \geq 10, \text{ and } \exists i \in \mathbb{N}, \text{s.t.} 10 \leq i \leq |w|, \text{s.t.} w[i-10:i] \text{ has more 1s than 0s}\}.\] Note we use Python syntax (0-indexing and slicing). I.e. $w = w_0w_1w_2...w_{|w|-1}$, and $w[i-10:i]$ refers to the substring $w_{i-10}w_{i-9},...,w_{i-1}$.

Solution

Let $X = \{w: w \text{ contains 101 as a substring} \}$, $Y = \{w: w \text{ has even length}\}$. Here’s a regular expression for $X$: $\Sigma^*101\Sigma^*$, and here’s a regular expression for $Y$: $(\Sigma\Sigma)^*$. Thus, both $X$ and $Y$ are regular. Then $A_{1}$ is the symmetric difference of $X$ and $Y$, and regular languages are closed under symmetric difference by HW5.
Here’s a DFA
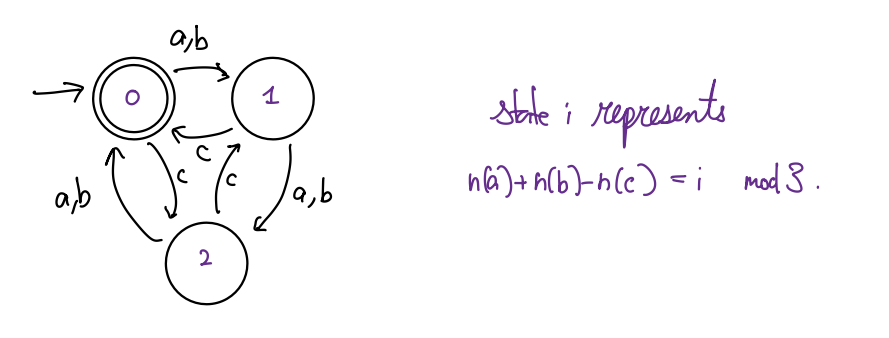
This language is finite and hence regular.
This language is not regular. Consider $S = \{0^3n: n \in \mathbb{N}\}$, by the Myhill-Nerode Theorem, it suffices to show that $S$ is infinite and pairwise distinguishable relative to $A_{4}$. First of all, $S$ is infinite since it has at least one element of every natural number, and there are an infinite number of natural numbers. Let $x$ and $y$ be elements of $S$, with $x \neq y$. Then $x = 0^{3i}$, and $y = 0^{3j}$ for some $i, j \in \mathbb{N}$ with $i \neq j$. Then $x1^{3i} \in A_{4}$ since it has $3i$ 0s and $3i$ 1s and a total of $6i$ characters which is divisible by $3$. however, $y1^{3i} \notin A_{4}$ since it has an unequal number of 0s and 1s. Thus, $S$ is pairwise distinguishable, as required.
Let $X = \{w : w \in \Sigma^*, |w| = 10, w \text{ has more 1s than 0s}\}$. Since $X$ is finite, $X$ has some regular expression $R$. Then $A_{5}$ has the following regular expression: $\Sigma^* R \Sigma^*$.

3 Handwriting

Simplify the act of handwriting English characters (not including punctuation) by drawing either lines or dots (i.e., the only dots are for ‘i’ and ‘j’).

Represent this with the alphabet $\Sigma = \{* , |\}$. Where $*$ represents a dot and $|$ represents any line that is not a dot.

People have different ways of writing.

Joe writes $i$ and $j$ as $|*$. I.e., Joe always dots the is and js immediately after writing the stem.
Kay dots the $i$ and $j$s before drawing the stem. I.e. Kay writes $i$ and $j$ as $* |$
Victoria writes lines first until three dots need to be written, at which point she writes the three dots consecutively. If, in the end, there are still more dots to be drawn, she dots them at the end.
With perhaps the most egregious technique, Tiffany writes all the lines first and then all the dots.

The set of possible sequences of marks that Joe makes can be represented as follows.

\[\mathrm{Joe} = \{w\in \{*, |\}^*: w \text{ starts with $|$ and does not contain the substring **}\}\] \[\mathrm{Kay} = \{w\in \{*, |\}^*: w \text{ does not contain the substring ** and ends with $|$}\}\]

3.1

Prove that $\mathrm{Joe}$ is a regular language.

Solution

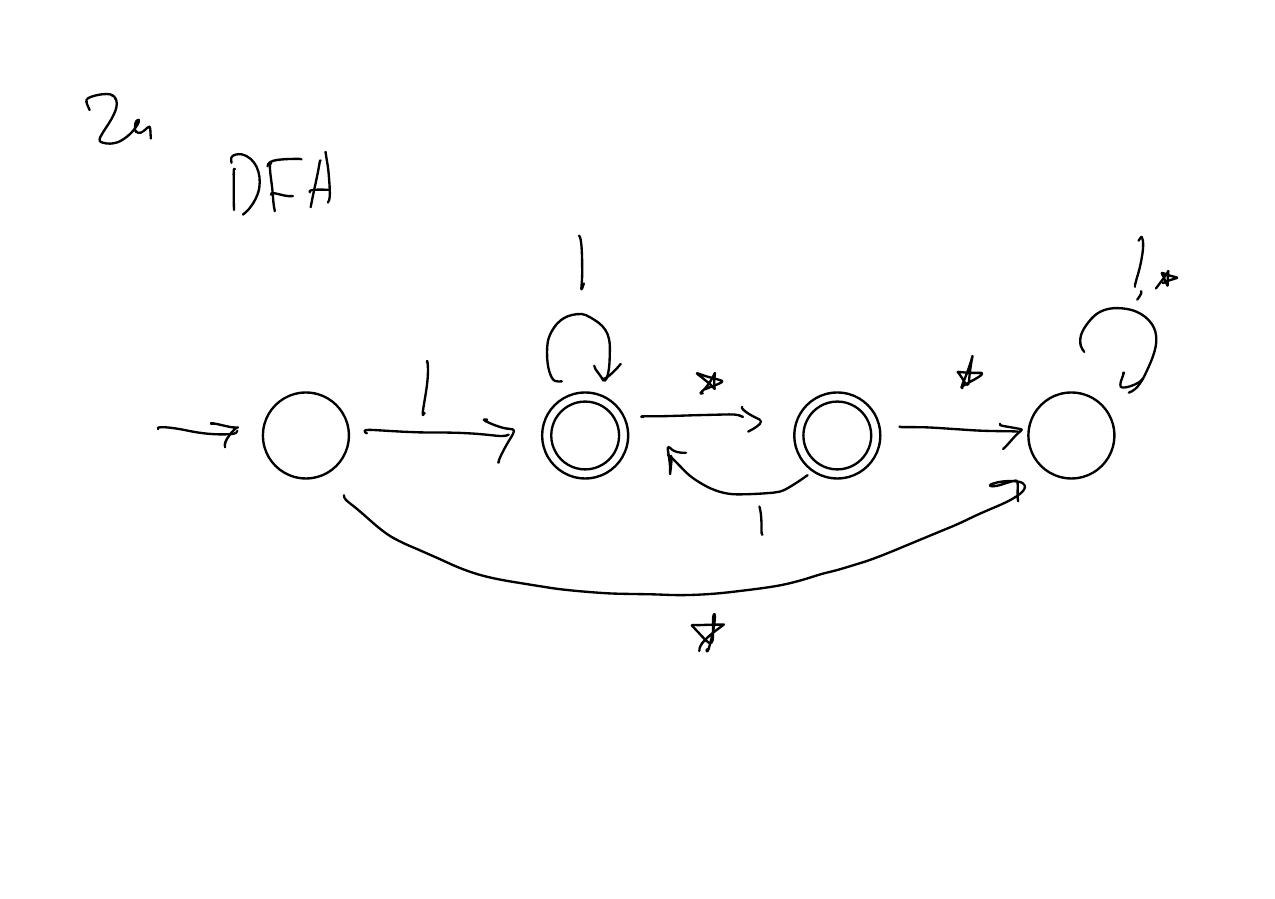
Similarly, $\mathrm{Kay}$ is also a regular language.

3.2

Formalize the set of sequences of possible marks that Tiffany makes. Is the language regular? Prove your answer.

Solution

$\mathrm{Tiffany} = \{|^n*^m: n, m \in \mathbb{N}, m \leq n\}$. The rule implies that all the dots follow all the lines. Since no character involves just a single dot, the number of dots is at most the number of lines. Finally, $|^n*^m$ for $m \leq n$ corresponds to writing a sequence of $m$ $i$s and $n - m$ $l$s.

$\mathrm{Tiffany}$ is not a regular language. Intuitively, I need to keep track of how many lines I have read, which requires infinite memory. Formally, we can prove this using the Myhill-Nerode theorem.

Let $S = \{|^n: n \in \mathbb{N}\}$ note that $S$ is an infinite set. Let $x, y \in S$ with $x \neq y$. Then $x = |^i, y = |^j$ for some $i \neq j$. WLOG assume $i < j$. Then $*^j$ is a distinguisher for $x$ and $y$ since $|^j*^j \in \mathrm{Tiffany}$ but $|^i*^j \notin \mathrm{Tiffany}$ since $j > i$ (too many dots). Thus, $\mathrm{Tiffany}$ is not a regular language.

3.3

Formalize the sequence of possible marks that Victoria makes. Is the language regular? Prove your answer.

Solution

There are many ways to do this - here’s a clean way.

For $i \in \{0,1,2,3\}$, define $A_i = \{|^n*^i: n \in \mathbb{N}, n \geq i\}$.

Then $\mathrm{Victorial} = A_3^* \circ (A_0 \cup A_1 \cup A_2)$.

Explanation: $A_i$ is the set of strings with at least $i$ lines followed by exactly $i$ dots. The $A_3^*$ part captures the fact that Victoria writes three dots in a row, and the $(A_0 \cup A_1 \cup A_2)$ part captures the last set of dots (which might not come in a multiple of 3).

To show that the language is regular, it suffices to show that each of the $A_i$s are regular.

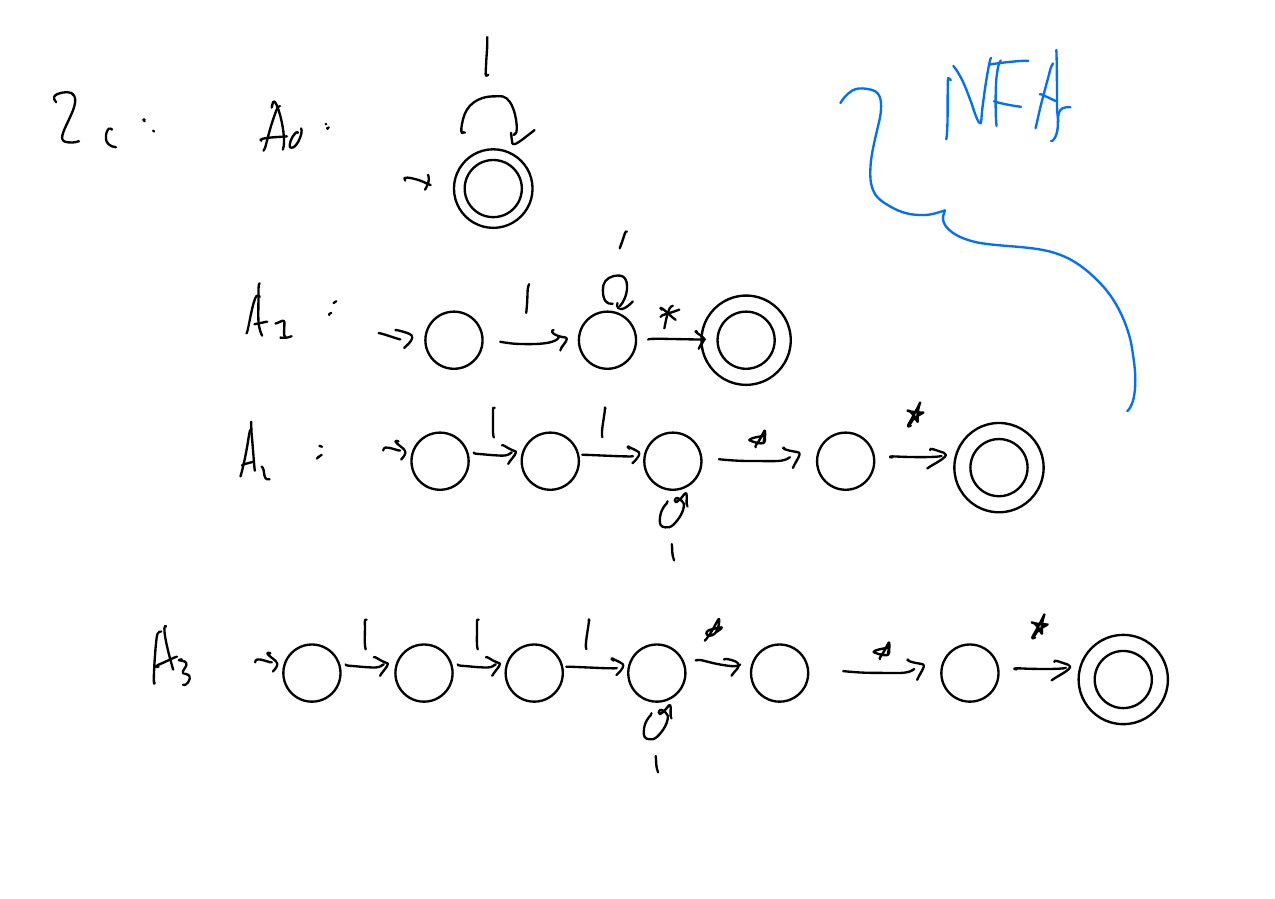
In this problem, for any set $A \subseteq\Sigma^*$, let $A_n = A \cap \Sigma^n$. I.e. $A_n$ is the subset of $A$ containing strings on length $n$.