Tutorial: Graphs
2025-05-21
1 Knights Walk

In this problem, the knight starts at some position on the chessboard and is trying to go to another position in the fewest number of hops possible.
For example, try to get the knight to the top right corner of the board in the fewest possible moves!
1.1
Exercise: Model this as one of the problems we learned from class.
Solution
Let \(G = (V, E)\).
Vertices: \(V = [8] \times [8]\)
Edges: \(E = \{\{(i, j), (k, l)\}: (k, l) \text{ is reachable from } (i, j) \text{ in one knight hop}\}\)
2 Knight’s Tour

In this problem, the knight starts at some ‘home’ position and tries to hop so that it hits every square exactly once.
2.1
Try it on 5x5.
2.2
Model the Knight’s Tour as one of the problems we learned from class.
Solution
The graph is the same as before. However, this time, we would like to find a Hamiltonian cycle in \(G\).
We can also model the knight’s tour problem as the Traveling Salesman by setting all edge weights to be \(1\).3 Independent Sets
Let \(G = (V, E)\) be a graph. A subset of vertices \(I \subseteq V\) is called an independent set if none of the vertices in \(I\) are adjacent. I.e. for all \(u, v \in I\), \(\{u, v\} \notin E\).
Example.
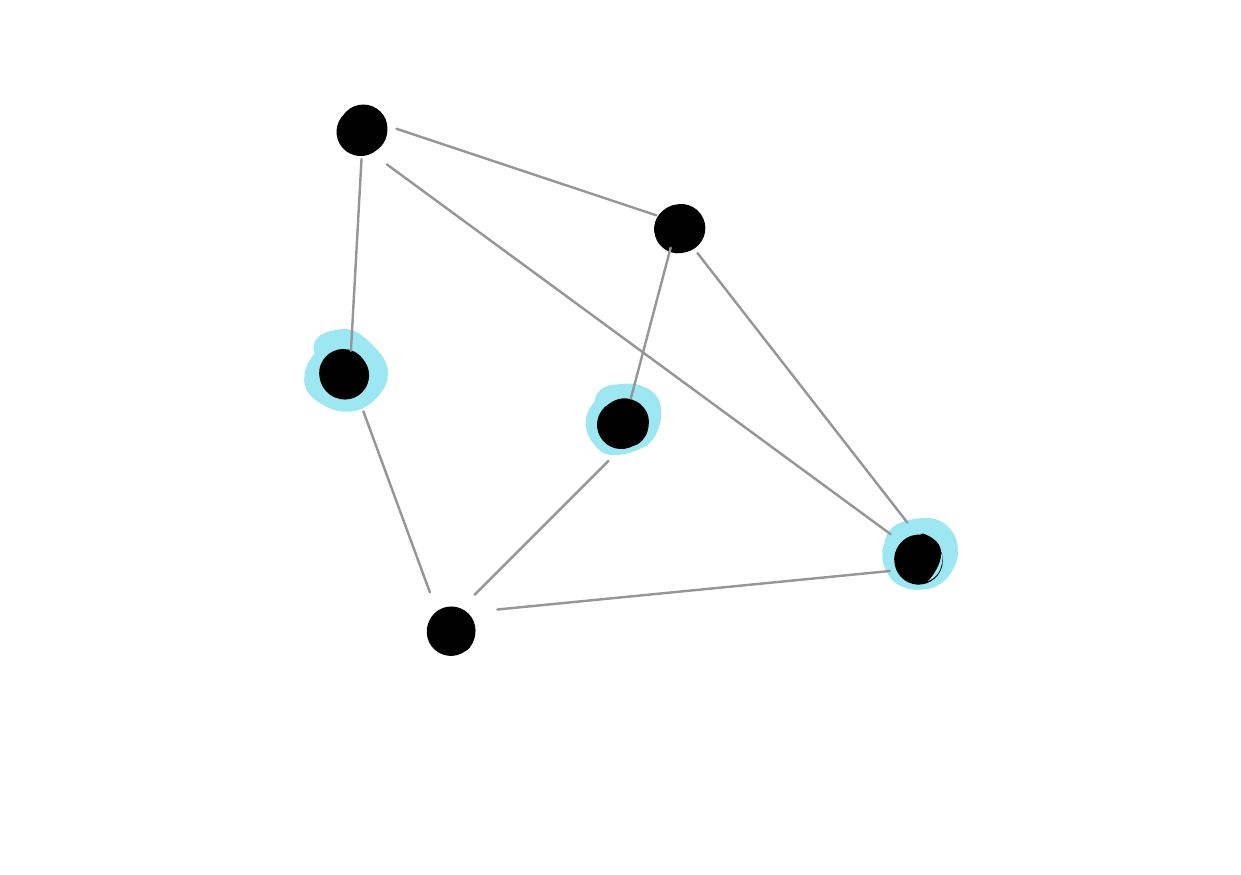
The nodes highlighted in blue form an independent set.
Here is the independent set problem:
Input: A graph \(G = (V, E)\), a number \(k \in \mathbb{N}\) with \(k > 1\).
Output: An independent set \(I \subseteq V\) in \(G\) of size \(k\).
Sometimes we don’t give a number \(k\) and ask for the largest possible independent set instead.
3.1
Imagine you are a high school teacher, and a large school fair is coming up. You need to organize students to do various tasks to help set up.
One task in particular - organizing the tables and chairs - will require a lot of collaboration and people to complete.
However, it being high school, you know that specific pairs of students DO NOT get along at all (let’s call them enemies), and if forced to work together, it will absolutely kill all productivity.
You want to find the largest possible set of students to work on organizing tables and chairs while making sure to avoid enemies working together on the task.
Exercise: Model this as an independent set problem
Solution
Define \(G = (V, E)\) as follows. Let \(V\) be the set of students. For every pair of distinct students \(u, v \in V\), the edge \(\{u, v\} \in E\) if and only if \(u\) and \(v\) are enemies.
Then, an independent set \(I\) in \(G\) is a set of students such that no two students in the set are enemies.
Finding the largest independent set then corresponds to finding the largest group of students to work on the task while ensuring that enemies don’t work together.4 Unique path
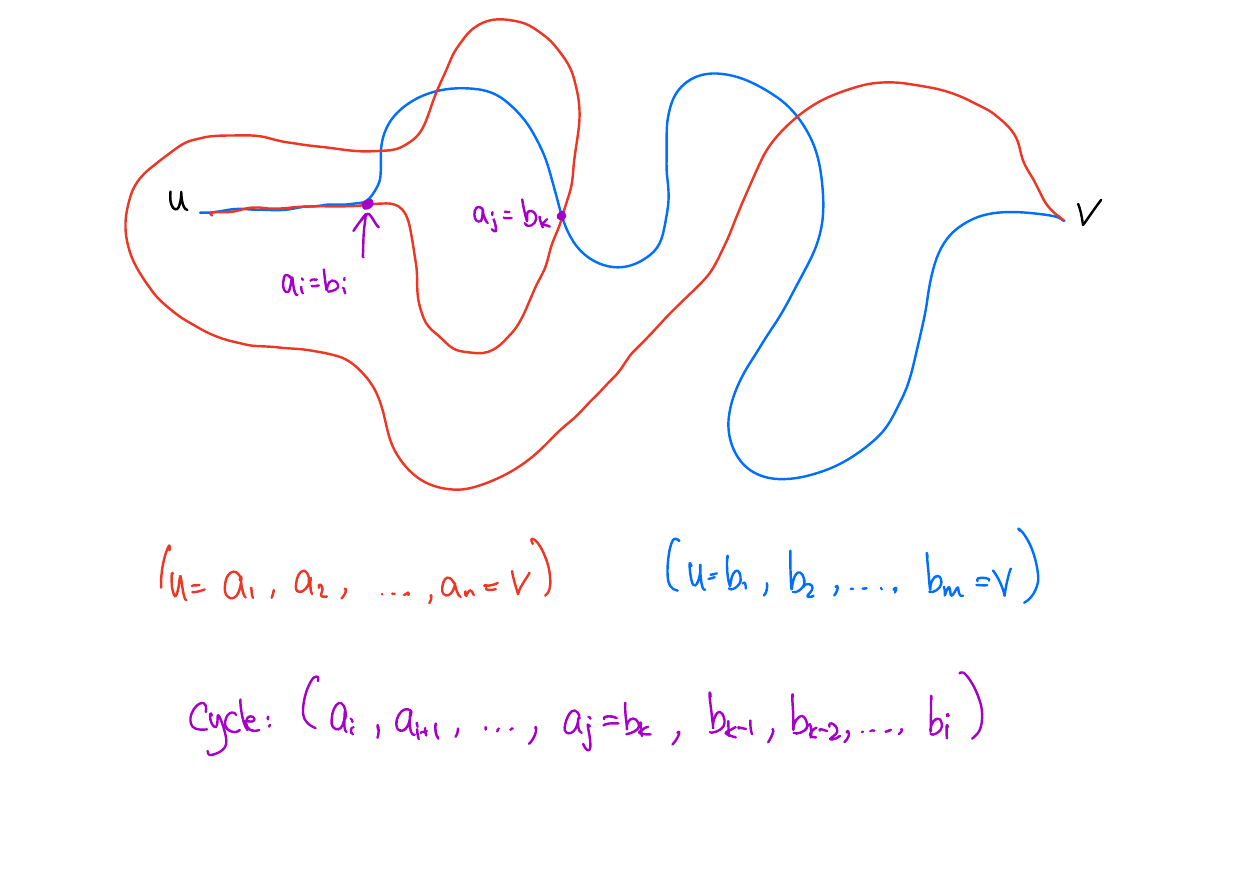
4.1
Let \(G = (V, E)\) be a tree (i.e. \(G\) is acyclic and connected). Show that for any distinct vertices \(u, v\) there is a unique path from \(u\) to \(v\).
Exercise: Prove this!
Solution
By contradiction, assume there are two distinct vertices \(u, v \in V\) and two distinct paths \(P_1 = (u=a_1,...,a_n=v)\) and \(P_2 = (u=b_1,...,b_m=v)\) from \(u\) to \(v\). We’ll show a contradiction by finding a cycle. Since \(P_1\) and \(P_2\) they paths must diverge at some point, i.e. there exists some \(i\) such that \(a_j = b_j\) for all \(j \leq i\), and \(a_{i+1} \neq b_{i+1}\).
Define \(S\) to be the set of vertices appearing in both paths after the \(i\)th vertex. Since both paths end at \(v\), \(|S| \geq 1\). Let \(j > i\) be the smallest number such that \(a_j \in S\). Let \(k\) be such that \(b_k = a_j\). Then I claim that
\[ C = (a_i, a_{i+1}, ..., a_j=b_k,b_{k-1},...,b_{i}=a_i) \]
is a cycle. Each of the edges in \(C\) is in the graph since \(P_1\) and \(P_2\) are paths. Furthermore, since we picked \(j\) to be the first vertex in \(P_1\) to appear in both paths after \(a_i\), no vertex other than \(a_i\) appears more than once in \(C\).
Here’s a picture: