Problem Set 4

Induction 2 + Part 1 Recap

1 Pairs

Let \(f_1, f_2\) be defined as follows

  • \(f_1((a, b)) = (b+1, a+1)\)
  • \(f_2((a, b)) = (2b, a+1)\)

Let \(X\) be the set generated from \(\{(0,1)\}\), by \(\{f_1,f_2\}\). Show \[\forall (a, b) \in X. (a\cdot b \text{ is even, and } a + b \text{ is odd.})\]

Solution

We’ll show the following claim. \(\forall (a, b) \in X\), \(a\) is even and \(b\) is odd.

Note that this suffices since an even number times an odd number equals an even number, and an even number plus an odd number is odd.

By structural induction.

Base case. The base case holds because \(0\) is even and \(1\) is odd.

Inductive step. Let \((a, b) \in X\) and suppose \(a\) is even and \(b\) is odd. In particular, suppose \(a = 2p\) and \(b = 2q + 1\) for some \(p, q \in \mathbb{N}\). We will show the claim for \(f_1((a, b))\), and \(f_2((a, b))\)

  • \(f_1(a, b) = (b+1 , a+1)\). We have \(b+1 = 2q + 1 + 1 = 2(q + 1)\), so \(b+1\) is even. Also, \(a + 1 = 2p + 1\), so \(a+1\) is odd.

  • \(f_2(a, b) = (2b, a+1)\). \(2b\) is even. Also, \(a + 1 = 2p + 1\), so \(a+1\) is odd.

This completes the induction.

2 Ternary Trees

Consider a subset \(\mathcal B\) of binary trees recursively defined as follows:

  • a single node is a member of \(\mathcal B\);

  • if \(T_1, T_2\in \mathcal B\) and \(T_1, T_2\) have the same height, then the tree constructed by placing \(T_1\) and \(T_2\) under a new root node (as illustrated below on the left) is also a member of \(\mathcal B\);

  • nothing else belongs to \(\mathcal B\).

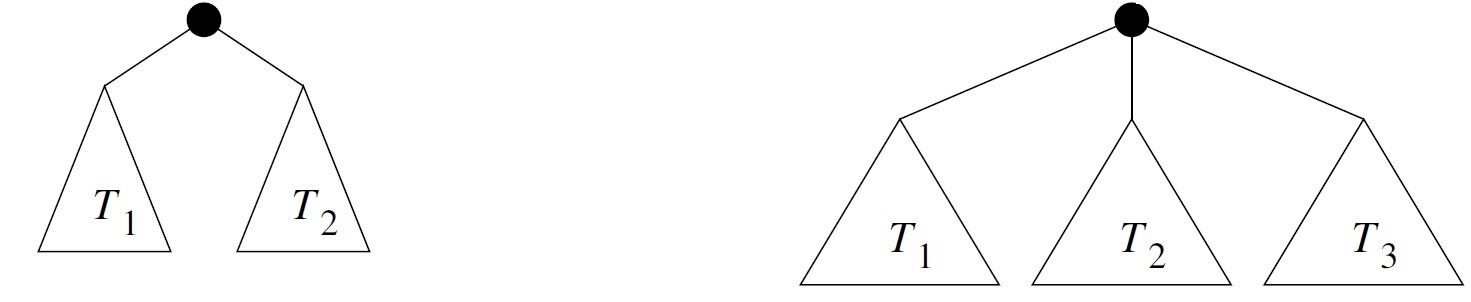
Also define a subset \(\mathcal C\) of ternary trees as follows:

  • a single node is a member of \(\mathcal C\);

  • if \(T_1, T_2, T_3\in \mathcal C\) and \(T_1, T_2, T_3\) have the same height, then the tree constructed by placing \(T_1\), \(T_2\), and \(T_3\) under a new root node (as illustrated above on the right) is also a member of \(\mathcal C\);

  • nothing else belongs to \(\mathcal C\).

Finally, we define the following terms.

  • A coloured tree is a tree in which every leaf node has been assigned one of two colours (red or blue). Only the leaves are coloured - internal nodes are colourless.

  • A leaves-subtree of a tree \(T\) is a subset of \(T\)’s leaves along with all of the leaves’ ancestors and the edges connecting them. Note that every ternary tree contains many binary leaves-subtrees.

  • A monochromatic binary tree is a coloured binary tree all of whose leaves are the same colour.

2.1

Prove that every colored tree \(T\in\mathcal C\) contains at least one monochromatic leaves-subtree which is a member of \(\mathcal B\). (For example, the coloured ternary tree on the left below, which is a member of \(\mathcal C\), contains a leaves-subtree, indicated on the right by thick edges and node outlines, which is monochromatic and is a member of \(\mathcal B\).)

Note that you cannot choose how the ternary tree is coloured. Rather, your proof must establish that the above statement is valid no matter how colours are assigned to the leaves of the ternary tree.

Solution

Also see Logan’s Walkthrough here.

\(P(T):\) arbitrarily coloured tree \(T\) contains a leaves-subtree \(T^\prime\in\mathcal B\) which is monochromatic.

The goal is to prove that for all \(T\in\mathcal C\), \(P(T)\) holds. Proof by structural induction on \(\mathcal C\).

Base Case: Let \(T\) be a single node. A single node is a member of \(\mathcal B\), and has a single colour assigned to it. Therefore, \(T\) is a member of \(\mathcal B\) which is monochromatic. Moreover, it is a leaves-subtree of itself. Therefore, \(T\) contains a leaves-subtree which is a member of \(\mathcal B\) and is monochromatic, and so \(P(T)\) holds.

Inductive Step: Let \(T_1, T_2, T_3\in\mathcal C\), and have the same height. By definition, \(\mathcal C\) includes a ternary tree \(T\) consisting of a root with \(T_1, T_2\) and \(T_3\) as subtrees.

Suppose \(P(T_1), P(T_2)\), and \(P(T_3)\). We’ll show \(P(T)\) holds. Since \(T_1, T_2\) and \(T_3\) have the same height, they contain binary leaves-subtrees of the same height. By IH, each of \(T_1, T_2\) and \(T_3\) respectively contain leaves-subtrees \(T_1^\prime, T_2^\prime, T_3^\prime\) which are monochromatic and are members of \(\mathcal B\). That is, \(T_1^\prime, T_2^\prime, T_3^\prime\in\mathcal B\), \(T_1^\prime, T_2^\prime, T_3^\prime\) have the same height, and all leaves of each \(T_1^\prime, T_2^\prime\) and \(T_3^\prime\) are coloured either red or blue.
Since there are 2 colours and 3 trees, by the pigeonhole principle, at least two of these monochromatic leaves-subtrees have to be of the same colour. Without loss of generality, let’s assume that all leaves of both \(T_1^\prime\) and \(T_2^\prime\) are red. In this case, \(T\) has a binary leaves-subtree \(T^\prime\) that is red. Namely, the one obtained by placing \(T_1^\prime\) and \(T_2^\prime\) under the root of \(T\). Since the root of \(T\) is not contained in \(T_1\) or \(T_2\), \(T^\prime\) is a member of \(\mathcal B\), by the recursive definition of \(\mathcal B\). By construction, \(T^\prime\) is a leaves-subtree of \(T\) and monochromatically red. Thus, \(P(T)\). So, by structural induction, for all \(T\in\mathcal C\), \(P(T)\) holds.

3 Round Robin

A round-robin tournament is a tournament in which every player plays a single game (rock-paper-scissors, tennis, chess, etc.) with every other player.

If \(V\) is a set of players, we encode the results of a tournament as a directed graph \(G = (V, E)\), \(E = \{(p, q) \in V \times V: p \text{ beats }q\}\)

3.1

Let \(G = (V, E)\) be a round-robin tournament. Here are two more definitions.

  • A player \(p\) is a winner if for all other players \(q\), either \(p\) beat \(q\) or \(p\) beat someone who beat \(q\).

  • A player \(p\) has a maximal number of wins if there is no other player \(q\) with strictly more wins than \(p\).

Is a player with the maximal number of wins always a winner? Prove your answer!

Solution

Let \(p\) be a player with the maximal number of wins, \(k\). By contradiction, suppose \(p\) is not a winner, that is, there is some \(q\) that \(p\) did not beat, and \(p\) did not beat anyone who beat \(q\). Let’s count the number of people \(q\) beat. \(q\) beat \(p\), AND everyone \(p\) beat, thus \(q\) beats at least \(k+1\) people, which is a contradiction to the fact that \(p\) is a player with the maximal number of wins.

3.2

Let \(G = (V, E)\) be any round-robin tournament encoded as a directed graph. Show that if \(|V| \geq 3\), and \(G\) has some cycle, \(G\) has a cycle of length exactly 3. Hint: Try the Well Ordering Principle!

Solution

Let \(P(n)\) be the predicate that is true if and only if for every round robin tournament \(G = (V, E)\) with \(|V| = n\) with a cycle has a cycle of length 3. We are trying to prove \(\forall n \in \mathbb{N}, n \geq 3. (P(n))\)

If \(|V| = 3\), and \(G\) has a cycle, it must be of length 3. Thus, \(P(3)\) holds.

By contradiction, assume the claim was false so that the set \(A = \{n \in \mathbb{N}: n \geq 3 \land \neg P(n)\}\) is non-empty. By the well ordering principle, \(A\) has some minimal element \(m\). Let \(G = (V, E)\) be a round robin tournament where \(|V| = m\), \(G\) has a cycle but no cycle of length \(3\). Let \((x_1,...,x_k)\) be a cycle in \(G\) with \(k \geq 4\). There are two cases.

  • If \((x_3, x_1) \in E\), then there is a cycle of length 3, namely \((x_1,x_2,x_3,x_1)\), which is a contradiction.

  • Otherwise, \((x_1, x_3) \in E\). Let \(G'\) be the graph obtained by throwing out \(x_2\). Then \((x_1,x_3,...,x_k)\) is a cycle in \(G'\), but there is still no cycle of length \(3\) in \(G'\) (throwing out a vertex does not create a new cycle). Vince \(G'\) has \(m-1\) vertices, \(m-1 \in A\), which contradicts the minimality of \(m\) in \(A\).

4 Rubik’s Inevitability

A Rubik’s cube is a fun puzzle/toy. If you don’t have a Rubik’s cube, check out this simulator.

Assume the blue face of the cube is always facing you. A state of the cube describes the current position of all the stickers. For example, the solved state of the cube is the one where every face has just one color (namely, the one matching the center square of the face).

The cube has \(6\) faces. Let \(f_i\) be the operation of turning the \(i\)th face of the cube a quarter turn clockwise. Let \(\mathrm{Turns}= \{f_1,...,f_6\}\) be the set of turns one can perform on the Rubik’s cube.

4.1

Let \(s\) be the solved state of the Rubik’s cube. Define the set of possible Rubiks cube states, \(\mathrm{Rubiks}\), recursively or inductively.

Solution

Also see Logan’s Walkthrough here.

\(\mathrm{Rubiks}\) is the smallest set such that

  • \(s \in \mathrm{Rubiks}\)

  • If \(x \in \mathrm{Rubiks}\), then \(\forall i \in [6]\), \(f_i(x) \in \mathrm{Rubiks}\).

Alternatively: \(\mathrm{Rubiks}\) is the set generated by \(\{s\}\) and \(\mathrm{Turns}\).

4.2

Model the task of solving a Rubik’s cube in the minimum number of moves as a graph problem. Fully specify the vertex set, edge set, and edge weights (if any), and explain why a solution to the graph problem corresponds to solving the cube.

Solution

Let \(s \in \mathrm{Rubiks}\) be the solved state of the cube. Define the following directed graph \(G = (\mathrm{Rubiks}, E)\) where for any states \(x, y \in \mathrm{Rubiks}\),

\[(x , y) \in E \iff \exists f \in \mathrm{Turns}. (f(x) = y).\] I.e. there’s an edge from \(x\) to \(y\) if and only if you can reach state \(y\) from state \(x\) with one turn.

A path in the \(G\) from \((x_1,...,x_n)\) corresponds to a sequence of turns, that takes the cube from state \(x_1\) to state \(x_n\). Thus, the problem of solving a Rubik’s cube from a scrambled state \(r\) in the fewest number of turns corresponds to the shortest path problem on input \(G\), starting vertex \(r\), and end vertex \(s\).

Start with a solved Rubik’s cube and consider any fixed sequence of turns. Now repeat that sequence of turns many times. Eventually, somewhat magically, the Rubik’s cube will return to the solved configuration! In this problem, we will prove this fact.

4.3

Let \(g\) be an aribitrary sequence of turns. Show \(g : \mathrm{Rubiks} \to \mathrm{Rubiks}\) is injective function.

Hint 1. Represent \(g\) as a composition of functions in \(\mathrm{Turns}\).
Hint 2. Show that each function in \(\mathrm{Turns}\) is injective.
Hint 3. Show by induction on \(n\) that the composition of \(n\) injective functions is injective.
Solution

Note that each \(f_i \in \mathrm{Turns}\) is injective, since each each turn \(f_i\) has a left inverse, namely \(f_i^3\). \(f_i^3\) is the function that applies \(f_i\) three times, i.e. a 270 degree turn, which is equivalent to a 90 degree turn in the counterclockwise direction, and clearly this undoes a 90 degree turn in the clockwise direction. I.e. \(f^3_i \circ f_i(x) = x\) for all \(x \in \mathrm{Rubiks}\). Thus, by HW1, \(f_i\) is injective.

Let \(g\) be an arbitrary sequence of turns. We can represent \(g: \mathrm{Rubiks} \to \mathrm{Rubiks}\) as a composition of functions in \(\mathrm{Turns}\). To show that \(g\) is injective, we will show that the composition of \(n\) injective functions is injective, for any \(n \in \mathbb{N}\).

Let \(P(n)\) be the predicate: For any sequence of \(k\) functions \(f_1,...,f_k \in \mathrm{Turns}\), the composition \(f_k \circ f_{k-1}\circ ... \circ f_1\) is injective. We’ll show \(\forall n \in \mathbb{N}, n \geq 1. P(n)\) holds.

By induction.

Base case. For \(n = 1\), let \(f_1 \in \mathrm{Turns}\). By the previous part, \(f_1\) is injective, thus the base case holds.

Inductive step. Let \(k \in \mathbb{N}, k \geq 1\) be any natural number at least 1, and assume \(P(k)\). Let \(f_1,...,f_{k+1} \in \mathrm{Turns}\) be a sequence of \(k+1\) functions. Let \(h = f_{k} \circ f_{k-1} \circ ... \circ f_{1}\). By the induction hypothesis, since \(h\) is the composition of \(k\) functions in \(\mathrm{Turns}\), \(h\) is injective. Then \(f_{k+1} \circ f_{k} \circ f_{k-1} \circ ... \circ f_{1} = f_{k+1} \circ h\). Since \(f_{k+1} \in \mathrm{Turns}\) and is injective by the previous part, and \(h\) is injective, and the composition of two injective functions is injective (by HW1), \(f_{k+1} \circ f_{k} \circ f_{k-1} \circ ... \circ f_{1}\) is injective as required.

4.4

Give an upper bound on \(|\mathrm{Rubiks}|\) i.e. find some \(k\) such that \(|\mathrm{Rubiks}| \leq k\)

Solution

There are 6 colors on the Rubik’s Cube, and \(9 \times 6 = 54\) stickers. Thus, there are at most

\[6^{54}\]

states of the Rubik’s Cube (each sticker can be one of 6 colors).[^2]

Let \(g\) be an arbitrary sequence of turns. Denote \[g^m = g\underbrace{\circ ... \circ}_{m \text{ times}}g\] to be the function that applies \(g\) \(m\) times. Also, let \(s \in \mathrm{Rubiks}\) be the solved state of the cube.

4.5

Show that for some \(m \in \mathbb{N}\) with \(m \geq 1\), \(g^m(s) = s\). That is, after \(m\) applications of the seqeunce of moves defined by \(g\), we return to the solved state!

Hint: Consider the sequence \(s_0, s_1, s_2,...\) where \(s_0 = s\), and \(s_i = g^i(s)\).

Solution

Let \(g\) be any sequence of turns. Let \(k\) be the upper bound on \(\mathrm{Rubiks}\). Let \(s = s_0\) be the solved state and \(s_0,...,s_k \in \mathrm{Rubiks}\) be the sequence of states obtained by repeatedly applying \(g\). I.e. for \(i \in \mathbb{N}i \geq 1\), \(s_i = g^i(s)\).

Note that since there are \(k+1\) states in the sequence, and \(|\mathrm{Rubiks}| \leq k\), by the pigeonhole principle, there is at least one state that appears at least twice in the sequence. Let \(m \in \mathbb{N}\) with \(m \leq k\) be the first index for which the sequence \(s_0,...,s_m\) has some state appearing twice. I.e. \(s_0,...,s_{m-1}\) are distinct and \(s_m = s_i\) for some \(i \in \mathbb{N}\), \(i < m\).

We’ll show that \(i\) must be \(0\). By contradiction, suppose \(s_m = s_i\) for some \(i > 0\). Then \(g(s_{i-1}) = g(s_{m-1})\). Since \(i < m\), and \(m\) is the first index for which there is a repeated state, \(s_{i-1} \neq s_{m-1}\) - but this contradicts the fact that \(g\) is injective!

Thus, \(g^m(s) = s\).

5 Cycles (optional)

For any function \(f: A \to A\), define the directed graph \(G_f = (A, E)\) where \((x, y) \in E\) if and only if \(f(x) = y\).

For this problem, we allow self-loops in directed graphs, i.e. \((x, x)\) can be an edge. Furthemore, we expand the definition of cycles to include cycles of length 1 (i.e a self-loop), and length 2 (i.e. two vertices \(x\) and \(y\) such that \((x, y) \in E\) and \((y, x) \in E\)).

What you just showed in the previous problem is in fact a special case of a more general result.

Theorem 1 Let \(A\) be any finite set and suppose \(f: A \to A\) is injective. Then the directed graph \(G_f = (A, E)\) consists entirely of disjoint cycles1.

5.1

Prove the theorem.

Footnotes

  1. By disjoint cycles, we mean that no vertex in \(G_f\) is contained in more than one cycle.↩︎