PROBABILISTIC MODELING OF NATURAL IMAGES

Several studies of natural image statistics have shown that natural images (like those taken by people with their camera) have peculiar properties. For instance, images tend to be very smooth. Understanding these properties is important for advancing our understanding of human perception as well as for many practical applications.

Probabilistic models of images have been a popular tool to capture these properties. A natural way to assess the quality of a probabilistic model is to draw samples from it. Unfortunately, current parametric models generate samples that are very different from natural images.

The aim of this project is to improve the generation quality of probabilistic models of natural images. There have been two leading approaches to the design of generative models of images that have latent variables. The simplest one and most primitive (e.g. factor analysis, sparse coding and Gaussian RBM) assumes that the data is conditionally generated using a spherical Gaussian distribution, ignoring the strong spatial correlations between neighboring pixels. The other approach has been to model this distribution with a zero-mean full covariance Gaussian distribution (see the Product of Student's t (PoT) model and covariance RBM (cRBM) model proposed in our AISTATS 2010 paper). In this project we put together these two approaches and use a conditional distribution that is the product of two Gaussians, one spherical but with a non-zero mean, and one that has zero-mean but with full covariance. The resulting distribution is again a Gaussian with a mean and a covariance that depend on the state of the latent variables. We have therefore extended PoT in mean-PoT (mPoT) and cRBM in mean-cRBM (mcRBM).

The model can also be interpreted as a gated Markov Random Field, because the pair-wise couplings between pixels and their biases are modulated, or gated, by the state of the latent variables.

The figure below shows some natural image patches of size 16x16 pixels used for training (on the left) and some samples drawn from the mcRBM model (on the right). Samples exhibit long range structures, smooth regions and sharp edges.

SPARSE CODING

For instance, Gabor Wavelets produce a sparse representation of natural images. A sparse coding algorithm is not only able to produce a similar sparse representation, but also, it adapts the analysis and synthesis transformations to the data (for instance, the filter banks used in the decomposition).

LEARNING INVARIANT REPRESENTATIONS

A sparse coding algorithm can be modified to learn representations that are not only sparse, but also invariant to some transformation. Invariance can be learned by adding terms to the loss function that is minimized during training (see our CVPR 2009 paper), exploiting the knowledge we have about the transformation, or exploiting general properties like temporal coherence in consecutive video frames or spatial stationarity in static images, for instance. Another possibility is to change the architecture of the system to produce the transformation we want (as in the method described in our CVPR 2007 paper); here is an example of this:

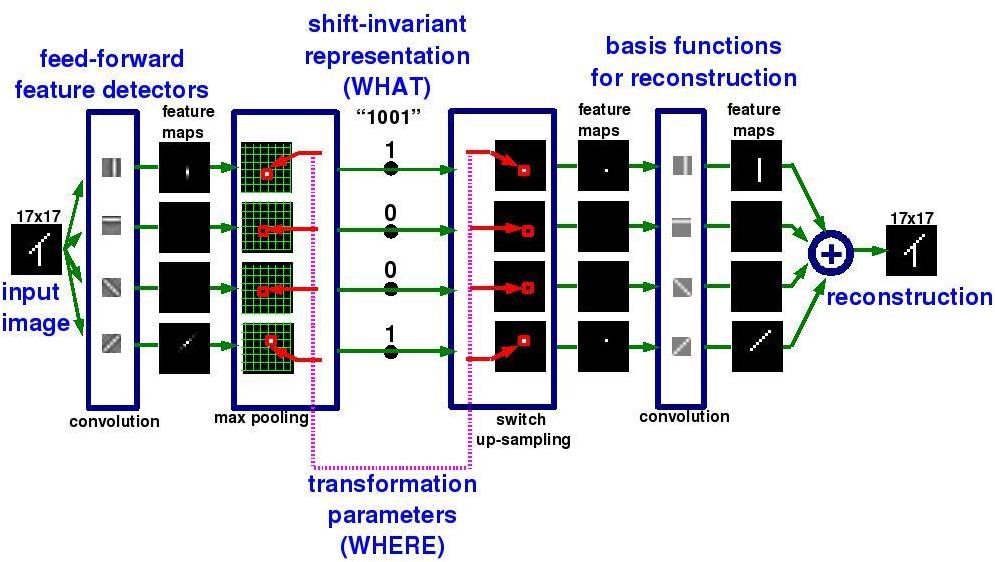
Consider the problem of detecting the orientation of bars placed at random locations in a binary image. The feed-forward path has a filter bank (that is learned) detecting bars in each possible orientation. By taking the largest value in the output map produced by each filter detector, we have a representation that is invariant to shifts. In the figure, the first filter is detecting vertical bars. No matter where a vertical bar is located, the largest value of the convolution of the input with this filter will be always the same (hence, the invariance to shifts). Since during training the filters are learned by reconstructing the input from the representation, we have to be able to recover the information about the location of the bar in order to generate good reconstructions. Hence, we store the position of the largest values in another set of variables, called the "transformation parameters". The feed-back path will be able to reconstruct the input by using not only the sparse and shift invariant representation, but also, the transformation parameters that specify where the features where found in the image.

LEARNING DEEP HIERARCHIES OF FEATURES WITH APPLICATIONS TO OBJECT RECOGNITION

The unsupervised learning algorithms that have been previously described can be used as building block to train deep networks in a layer-wise fashion. Once a layer has been trained, it used to produce the input to train the layer above. Hinton et al. (Neural Computation 2006) have a nice variational bound argument to explain why this procedures is a sensible thing to do.

Deep models have an important computational advantage. A deep model can re-use intermediate representations to learn more abstract representations that, hopefully, are more easily correlated with the underlying causes generating the data.

The figure below shows the performance of our earlest visual recognition system on a few categories of objects from the Caltech 101 dataset.

MODELING ACOUSTIC SIGNALS WITH APPLICATIONS TO RECOGNITION

In this project my collegues and I applied Deep Belief Nets to spectrograms and achieved the best reported results (to date of publication) on the speaker-independent TIMIT phone recognition task!

IMAGE DENOISING AND COMPRESSION

Sparse coding algorithms can also be used to denoise images. Assuming we know a model for the corruption process (e.g. additive Gaussian noise), then we can train the forward path of the model to map noisy inputs to a sparse representation, and we can force the feed-back path to reconstruct the original un-corrupted input from the sparse representation. After training, the model has learned to denoise images by first mapping the input into a sparse representation, and then, by mapping back the sparse representation into input space through the transformation given by the feed-back path. Since a sparse representation concentrates the energy in a few coefficients, the noise added to the input causes the representation to change very little in terms of the relative magnitude between active and approximately zero coefficients, yielding good results in denoising.

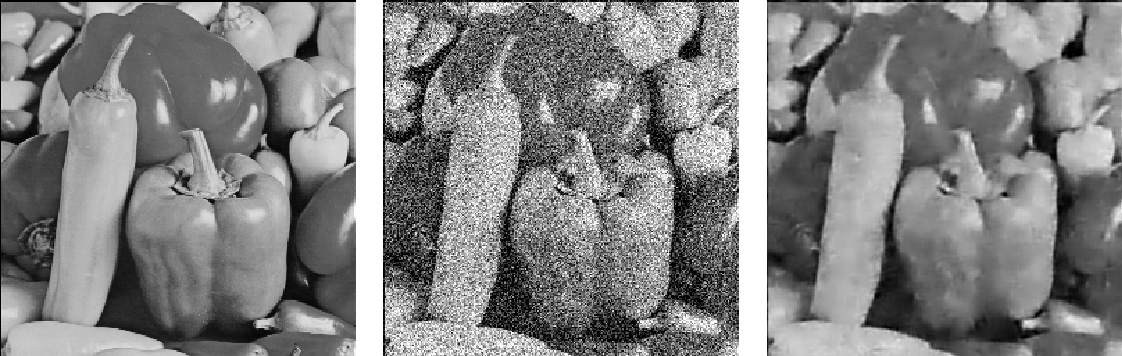
Our experiments reported state-of-the-art performance in denoising of natural images corrupted by additive Gaussian noise for medium and high levels of noise. The figure below shows an example. The original image is on the left, the corrupted image is in the middle, and the denoised image in on the right.

We also did experiments in text document image compression. After learning sparse representations of document images, a page is compressed by encoding the representation and the location of patches that contain characters. An example of document image reconstruction is given below (compression ratio equal to 95, percentage of flipped pixels 1.35%).

TEXT RETRIEVAL AND CLASSIFICATION

I devised a Semi-Supervised algorithm to learn text document representations, and used these representations for classification and retrieval tasks. Nowadays the most popular document representation is the bag-of-word representation storing the number of times each word of the dictionary appears in a given document. This is conceivably sub-optimal because it assumes that words are independent of each other, disregarding synonyms and polysemous words.

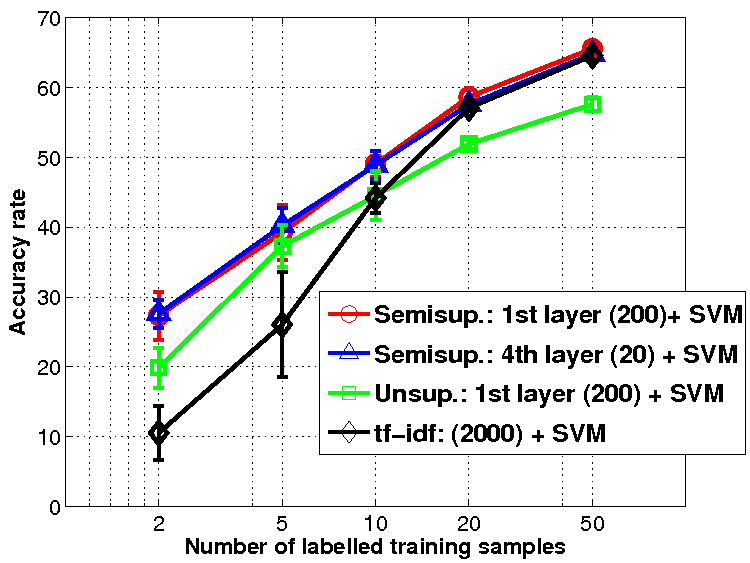
In this work, I have developed an algorithm to train a deep network that extracts representations of documents. Training proceeds by minimizing an objective function that combines both an unsupervised term enforcing good reconstruction of the input from the representation, and a supervised term requiring the representation to be predictive of the document label (e.g. the topic). The figure on the left shows that a representation that has been learned by combining both objectives outperforms the re-weighted input bag-of-word representation (tf-idf) as well as the representation produced by the same algorithm, but trained totally unsupervised (20 Newsgroup dataset). Also, the performance does not degrade significantly if we compress the representation as we go from the first to the last layer. In this experiment the first layer produces a 200-dimensional representation, while the top layer a representation with just 20 components. If the last layer of the deep network has only two components, then we can map the data into the plane for visualization. The figure on the right shows the learned mapping for the documents of the Ohsumed dataset (medical abstracts). The input 30,000-dimensional space is mapped into the plane in such a way that documents belonging to the same class are clustered together, and similar topics are placed next to each other.

ENERGY-BASED MODELS

The Energy-Based Model is a framework for devising efficient learning algorithms. In the supervised case an energy is associated to each pair of input sample and target value. Inference consists of minimizing the energy with respect to the target, and learning consists of defining a loss functional, which is a function of the energy, whose minimization yields the desired behavior, i.e. the energy is lower for the target that corresponds to the true label. Probabilistic models are an instance of Energy-Based Models and they correspond to models that are trained with a particular choice of loss functional, the negative of the log-likelihood, which is often intractable to compute. Energy-Based Models are useful in high-dimensional spaces when the normalization requirement imposed by probabilistic models become computationally intractable. In some sense, Energy-Based Models can be interpreted as a “local probabilistic model”, because they change the model distribution only around regions of interest, like those populated by training samples. There are conditions on the energy and the loss functional that guarantee learning and correct inference. Also, there are extensions to the case in which models have latent variables. The figure below shows the energy function of two models trained with different loss functionals. Despite the different shape of energy, the two models achieve the same goal, i.e. they give lower energy to the training samples (the blue dots).

In Unsupervised Learning labels are not provided. Therefore, the energy is a function of the input data, and maybe some other latent variable. The goal of learning is to assign lower energy to samples that are similar to training samples, and higher energy to the other points in input space (or at least to those points that are in a neighborhood of the training samples). This problem can be interpreted as an “energy carving” problem because learning consists of adjusting the parameters of the model to carve the energy surface in such a way that training samples are always on the valleys of the surface (i.e. local minima). In general, it is not sufficient to adjust the parameters in such a way that only the energy of the training samples is decreased because it might well be that the energy surface becomes flat, corresponding to a model that cannot discriminate between points that are similar and points that are dissimilar to the training samples.

Some unsupervised learning algorithms are able to learn good energy surfaces by using a loss functional that has two terms. The first one decreases the energy of the training samples, while the second one increases the energy of a properly chosen point in input space. However, it might be difficult and computationally expensive to individuate a good candidate for pulling up the energy, overall in high-dimensional spaces. Other methods achieve the same goal of energy carving by replacing this explicit pull-up term in the loss, with constraints on the representation, such as sparsity for instance. By making sure that the internal representation of the model can carry only a limited amount of information, the energy surface can take the right shape without using a contrastive term in the loss functional. This can yield to the design of far more efficient unsupervised learning algorithms.

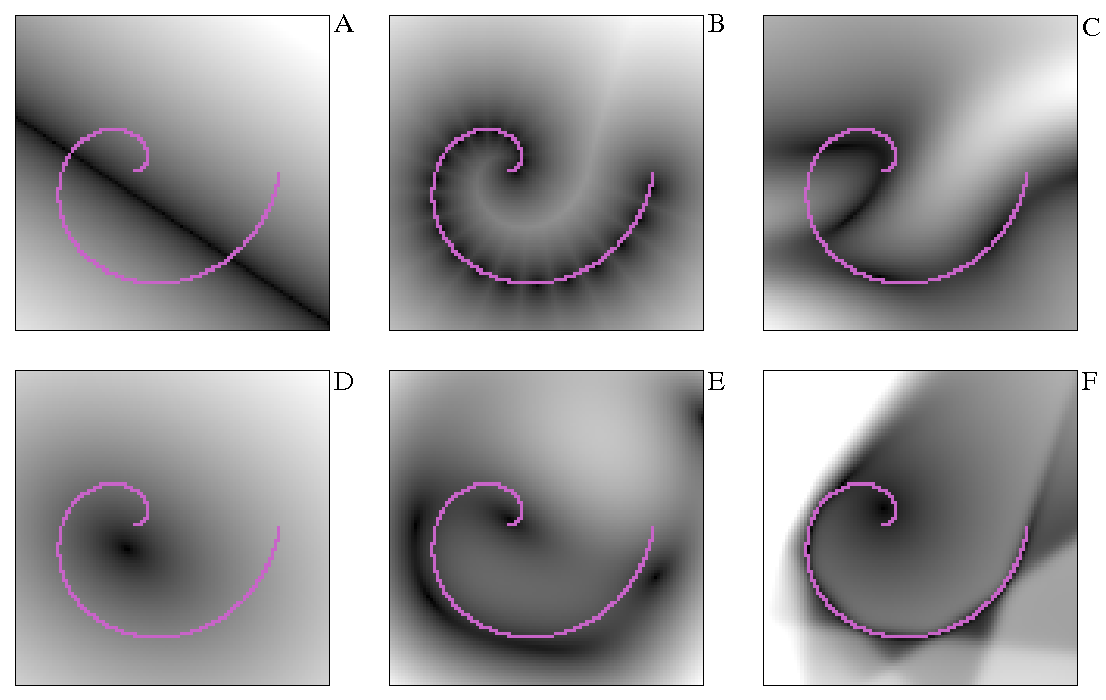
For instance, the figure below shows the energy surface (in this case the energy is the reconstruction error) produced by different algorithms after training on a dataset of points sampled from a spiral (the points in magenta). We can see the energy surface produced by A) PCA, B) K-Means, C) 2-1-2 auto-encoder neural net, D) 2-20-2 auto-encoder neural net trained by maximum likelihood, E) 2-20-2 auto-encoder neural net trained my maximum margin loss, and F) a 2-20-2 network trained with a sparse coding algorithm. All these algorithms are able to avoid flat energy surfaces, and the apparently very different shapes of these energies can be understood under the principle described above of explicit or implicit energy pull-up.

AUTONOMOUS ROBOT NAVIGATION

I developed several unsupervised learning algorithms to extract visual features for the DARPA project called LAGR (learning applied to ground robots). We used the learned features to do long range stereo helping the robot navigate in unknown outdoor environments.

AUTOMATIC RECOGNITION OF BIOLOGICAL PARTICLES

While I was at Caltech, I worked on a system for automatic recognition of biological particles in microscopic images, such as pollen grains and cells in human specimen. The system is composed of (1) a detector, and (2) a classifier assigning a particles to its category. The figure shows the tool I designed to collect the pollen data. After acquiring an image from the microscope, an expert had to detect and label the pollen grains. These were subsequently used to train the algorithm for automatic recognition. In this image, there are two Chinese elm pollen grains, the other particles are just debris.