NumPy Review. This tutorial gives a conceptual and practical introduction to Numpy. The code can be found here.
Dataset split. Kilian Weinberger's Cornell class CS4780 Lecture 3 starts to talk about proper dataset split at 2:00 until 24:00.
No free lunch. The same lecture touches on no free lunch theorem and algorithm choice starting at 27:10 until 33:30.
K-Nearest-Neigbors. The same lecture starts to talk about KNN at 36:00 until the end. The lecture note also has an easier to follow convergence proof for 1-NN in the middle of the page and it also has a nice demo of curse of dimensionality after that.
K-Nearest-Neigbors with Numpy. Prerecorded video going through the implementation of K-Nearest-Neigbors using Numpy. Code.
A very nice Probability Cheatsheet share by a student.
Information content and entropy. Video.
Snapshots We encourage you to watch the
whole video.
If you don't have enough time, you could consider watching it at 1.5x or 2x speed.
If you have trouble following this lecture, you can also watch their
first
lecture.
Further understanding of entropy and source coding theorem. Video.
Snapshots
We encourage you to watch the whole video.
If you don't have enough time, you could consider watching it at 1.5x or 2x speed.
More info theory. The concept of entropy is at the heart of information theory and also many machine learning methods, so it is important to have a thorough understanding of it. We will see two more different ways of explaining entropy. This tutorial first explain the concept of entropy from another way, and then nicely build on that to explain the concepts of cross entropy and KL divergence. This tutorial first explain the concept of entropy from yet another way, and then talk about information gain, and in the specific formulation in this tutorial it can also be interpreted as mutual information.
Eigen decomposition. Video. Transcript (The middle tab). We encourage you to watch the whole video.
Positive Definite and Semidefinite Matrices. Video. Transcript (The middle tab). He briefly discussed convexity and gradient descent here, you can just take it as a prelude as we'll be getting into more details about those topics later. We encourage you to watch the whole video.
SVD. Video. Transcript (The middle tab). I particularly like how he talked about the geometry of SVD starting from 28:50, even though there's a minor mistake there too. The mistake is the second step, multiplying the diagonal matrix of singular values. It should stretch along the standard basis, not along the rotated basis. In other words, the sigma should be applied on the x-y directions, not the rotated directions, you can refer to a correct picture on wikipedia here.
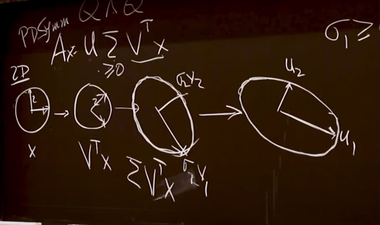
Screenshot from the lecture at 34:06
Gradient Descent intro, for logistic regression. Video.
Gradient Descent on multiple samples Video.
Vectorization. Video.
Gradient Descent for NN Video.
Backprop intuition Video.
Forward and backward propagation Video.
Gradient checking. Video.
Mini batch gradient descent Video.
Understanding mini batch gradient descent Video.
[Optional] More on optimization The no free lunch theorem states that any two optimization algorithms are equivalent when their performance is averaged across all possible problems. There are a lot of optimizers out there, and each could be the best under different situations. Here we introduce some of the most commonly used ones for your reference. Before that, you should have a intuitive understanding of exponentially weighted averages as it'll be used a lot in those methods: videos 1, 2, 3. After that, gradient descent with momentum, RMSProp, Adam. In this Adagrad video, there's also some nice visualizations of the behaviors of different optimizers on different loss landscapes. You can find the complete set of such visualizations here.
We'll go through this simple implementation of gradient descent during the tutorial: Code.
Decision tree. Please watch this lecture by Nando de Freitas to breifly review decision tree. Slides. If you don't have enough time, you could consider watching it at at 1.25x or 1.5x speed.
Random Forests. Please watch this lecture by Nando de Freitas. Slides. If you don't have enough time, you could consider watching it at at 1.25x or 1.5x speed.
Maximum Likelihood. We will go through some derivations on the maximum likelihood estimators during the tutorials.
More PCA (Optional). Here is a lecture that goes through the PCA derivation in great detail if you are interested
Pytorch. This tutorial gives an overview of pytorch and the basics on how to train neural net. Code.
Transfer Learning with pytorch (optional). The last part of the the same video briefly talks about transfer learning, it's optional.
Autograd (optional). This tutorial explains how autograd works in pytorch so that you can have a general idea of how the gradients are handled by pytorch.
This week we will cover two major types of deep generative models: VAEs and GANs and watch some lecture excerpts from by Pieter Abbeel (et al.) 's latest deep unsupervised learning course.
VAEs. Please watch this lecture from here to 1:46:00, where the foundational ideas of VAEs are covered. VAE might seem like a simple model but there are a lot of conceptually elegant ideas behind it. Notice how the the likelihood ratio gradient connects to the REINFORCE algorithm covered in this week's lecture, especially why it has huge variance. Everything (Variations and related ideas) after 1:46:00 is optional. Slides. Code used in the lecture.
GANs. Please watch this lecture from here to 0:57:00, where the foundational ideas of GANs are covered. Everything (More GANs) after it is optional. However if you ever use GAN in your project, you are encouraged to learn about the Gradient Penalty(GP) covered around 1:55:00. It is helpful not only for WGAN but also for almost any GAN setting. (Shown in papers 1(image), 2(waveform) and 3(text)), and it's very simple to implement, so you are encouraged to consider adding GP when you use GAN for your project. Slides. Code used in the lecture.
ML Project Workflow. By popular demand, we will talk about typical workflow for a ML project. This is usually something that's never taught, and one was just expected to know how to work on ML projects. As a result there are many types of workflows out there. The one introduced in this tutorial is Sheldon's typical workflow. It was based on and inspired by many of (past) collaborators and mentors, and special thanks to for.ai and UTMIST. The codebase. GitKraken. Note that if you are a student you have free access to github pro, which gives you full access to GitKraken pro. VS Code. You are not required to follow this workflow for your final project.
Self-Supervised Learning.
Please watch this lecture from here to 1:02:00, where the foundational ideas of self supervised learning in vision are covered.Final project. Slides
Website template. Any feedback is very appreciated, please reach out to: Sheldon, email: huang at cs dot toronto dot edu