Andrew Li
PhD Candidate, Computer Science
University of Toronto

Background

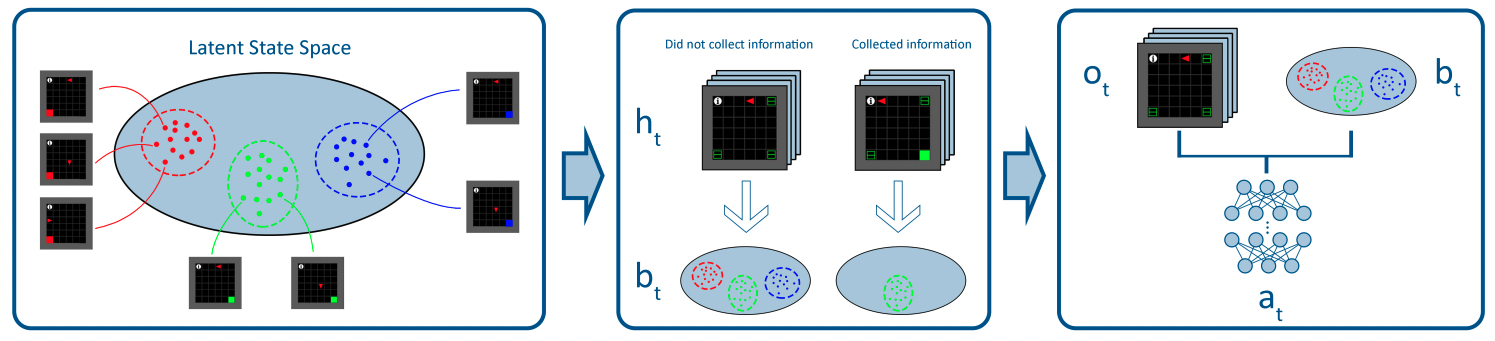
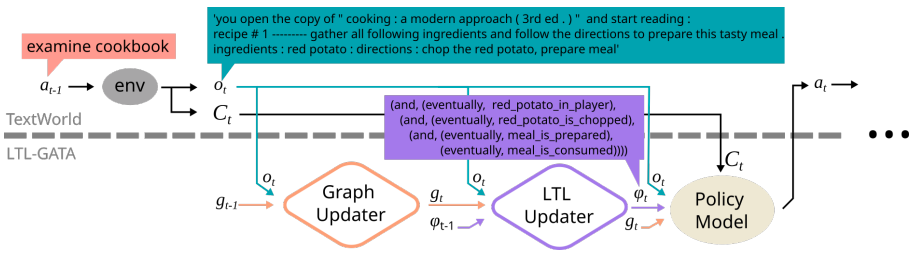
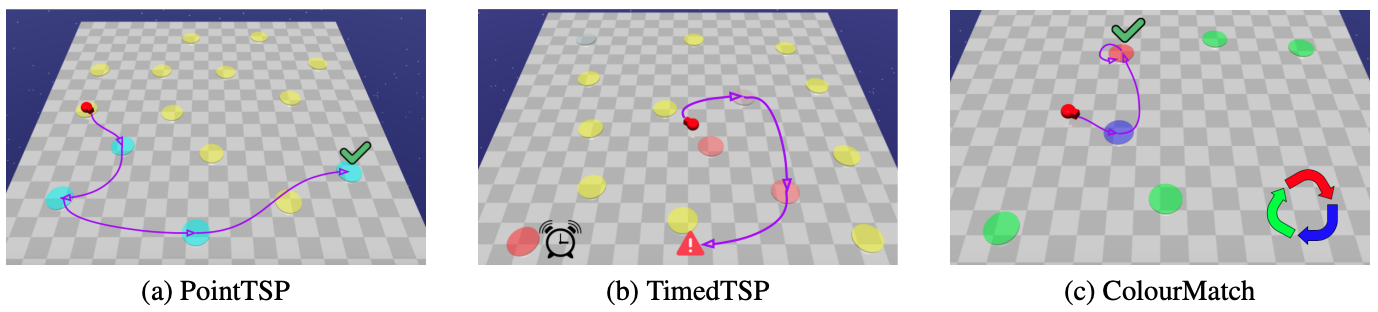
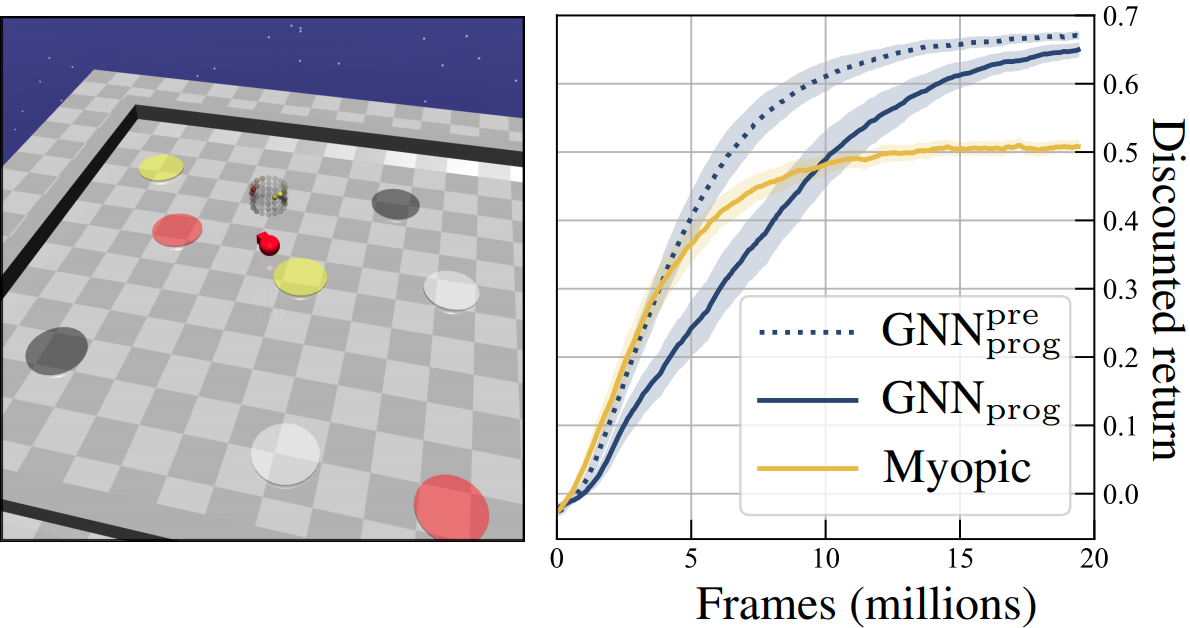
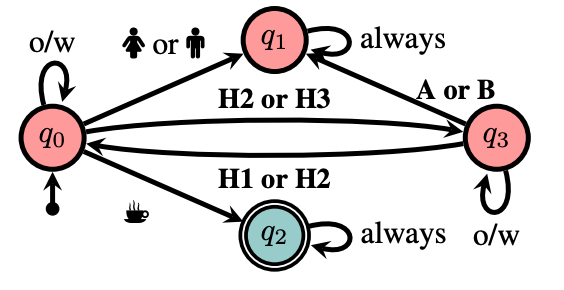
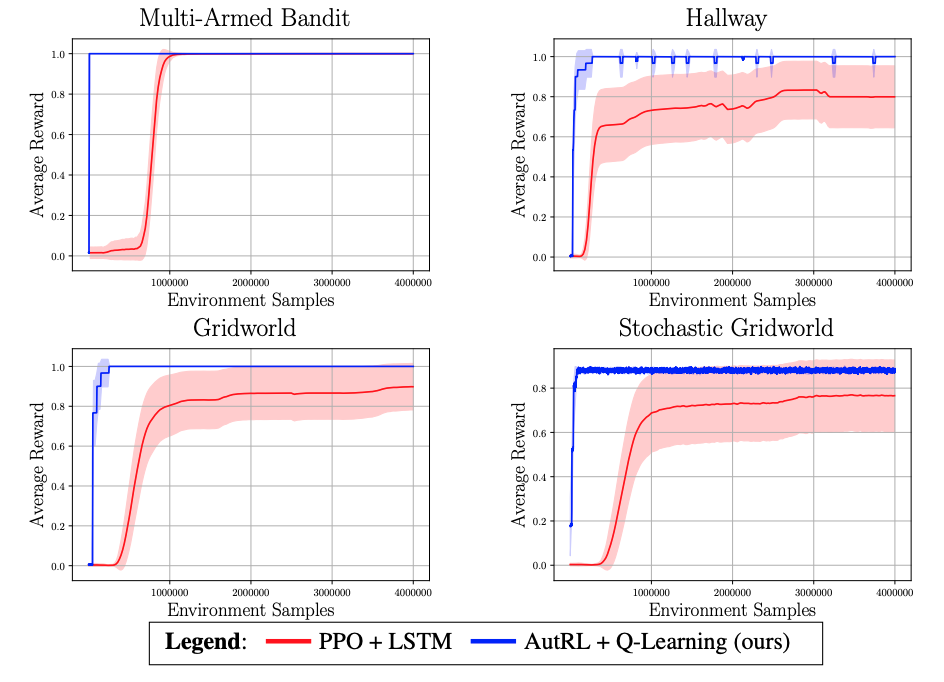
I am a final-year PhD student in Computer Science at the University of Toronto and the Vector Institute for Artificial Intelligence, supervised by Sheila McIlraith. My research interests lie at the intersection of machine learning (particularly reinforcement learning), AI planning, and knowledge representation & reasoning. I aim to develop AI that learns over a long lifetime by acquiring knowledge from its interactions with the world, abstracting knowledge into generalizable concepts, and reasoning at a high-level to robustly handle new situations.

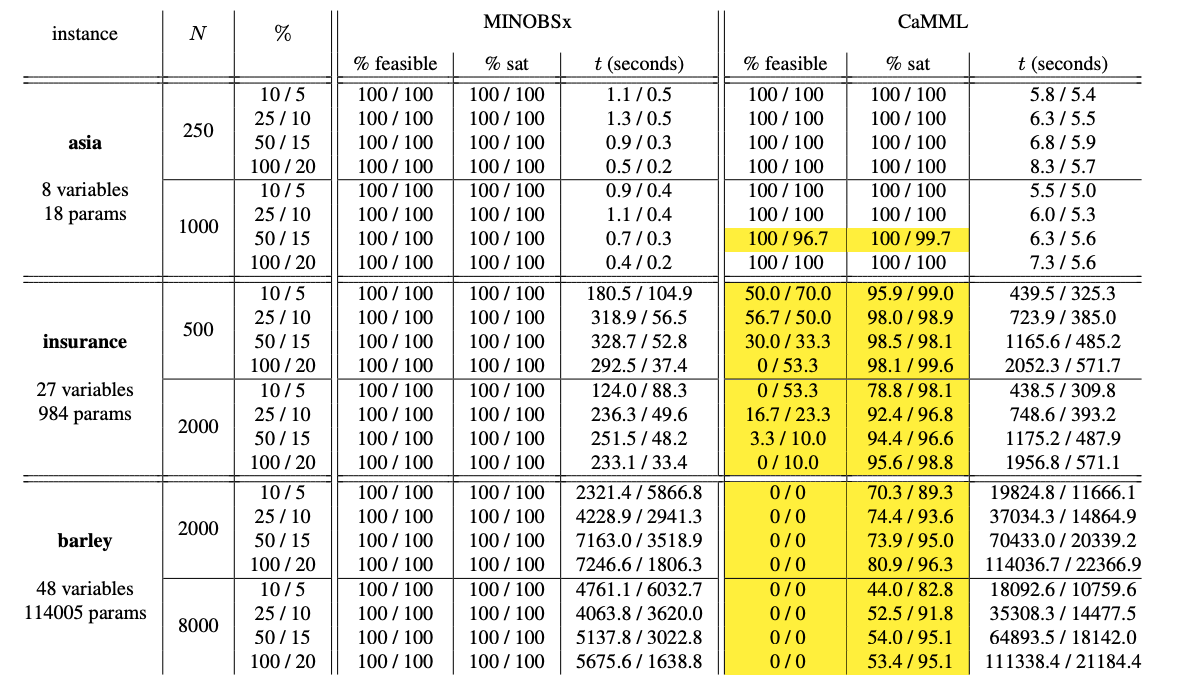
In 2023, I interned at Zoox, where I worked on reinforcement learning for autonomous driving. As an undergrad at the University of Waterloo, I researched combinatorial optimization algorithms for learning Bayesian network structures from data. Before that, I was one of the top competitive programmers in Canada.

Education

• Candidate for Ph.D. in Computer Science, 2021 - present
  University of Toronto
• M.Sc. in Computer Science, 2019 - 2021
  University of Toronto
• B.Math. in Computer Science, Combinatorics & Optimization (Double Major), 2015 - 2019
  University of Waterloo

Research

Research Statement (October 2024).

• Reward Machines for Deep RL in Noisy and Uncertain Environments   (NeurIPS 2024)

  by Andrew Li, Zizhao Chen, Pashootan Vaezipoor, Toryn Klassen, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Poster   Code

  Abstract: Reward Machines provide an automaton-inspired structure for specifying instructions, safety constraints, and other temporally extended reward-worthy behaviour. By exposing the underlying structure of a reward function, they enable the decomposition of an RL task, leading to impressive gains in sample efficiency. Although Reward Machines and similar formal specifications have a rich history of application towards sequential decision-making problems, they critically rely on a ground-truth interpretation of the domain-specific vocabulary that forms the building blocks of the reward function—such ground-truth interpretations are elusive in the real world due in part to partial observability and noisy sensing. In this work, we explore the use of Reward Machines for Deep RL in noisy and uncertain environments. We characterize this problem as a POMDP and propose a suite of RL algorithms that exploit task structure under uncertain interpretation of the domain-specific vocabulary. Through theory and experiments, we expose pitfalls in naive approaches to this problem while simultaneously demonstrating how task structure can be successfully leveraged under noisy interpretations of the vocabulary.

• Learning Belief Representations for Partially Observable Deep RL   (ICML 2023)

  by Andrew Wang*, Andrew Li*, Toryn Klassen, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Talk   Poster   Code

  Abstract: Many important real-world Reinforcement Learning (RL) problems involve partial observability and require policies with memory. Unfortunately, standard deep RL algorithms for partially observable settings typically condition on the full history of interactions and are notoriously difficult to train. We propose a novel deep, partially observable RL algorithm based on modelling belief states — a technique typically used when solving tabular POMDPs, but that has traditionally been difficult to apply to more complex environments. Our approach simplifies policy learning by leveraging state information at training time, that may not be available at deployment time. We do so in two ways: first, we decouple belief state modelling (via unsupervised learning) from policy optimization (via RL); and second, we propose a representation learning approach to capture a compact set of reward-relevant features of the state. Experiments demonstrate the efficacy of our approach on partially observable domains requiring information seeking and long-term memory.

• Learning to Follow Instructions in Text-Based Games   (NeurIPS 2022)

  by Mathieu Tuli, Andrew Li, Pashootan Vaezipoor, Toryn Klassen, Scott Sanner, Sheila McIlraith
  Paper   Poster   Code

  Abstract: Text-based games present a unique class of sequential decision making problem in which agents interact with a partially observable, simulated environment via actions and observations conveyed through natural language. Such observations typically include instructions that, in a reinforcement learning (RL) setting, can directly or indirectly guide a player towards completing reward-worthy tasks. In this work, we study the ability of RL agents to follow such instructions. We conduct experiments that show that the performance of state-of-the-art text-based game agents is largely unaffected by the presence or absence of such instructions, and that these agents are typically unable to execute tasks to completion. To further study and address the task of instruction following, we equip RL agents with an internal structured representation of natural language instructions in the form of Linear Temporal Logic (LTL), a formal language that is increasingly used for temporally extended reward specification in RL. Our framework both supports and highlights the benefit of understanding the temporal semantics of instructions and in measuring progress towards achievement of such a temporally extended behaviour. Experiments with 500+ games in TextWorld demonstrate the superior performance of our approach.

• Exploring Long-Horizon Reasoning with Deep RL in Combinatorially Hard Tasks   (Decision Awareness in RL Workshop @ ICML 2022)

  by Andrew Li, Pashootan Vaezipoor, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Poster   Code

  Abstract: Deep reinforcement learning has shown promise in discrete domains requiring complex reasoning, including games such as Chess, Go, and Hanabi. However, this type of reasoning is less often observed in long-horizon, continuous domains with high-dimensional observations, where instead RL research has predominantly focused on problems with simple high-level structure (e.g. opening a drawer or moving a robot as fast as possible). Inspired by combinatorially hard optimization problems, we propose a set of robotics tasks which admit many distinct solutions at the high-level, but require reasoning about states and rewards thousands of steps into the future for the best performance. Critically, while RL has traditionally suffered on complex, long-horizon tasks due to sparse rewards, our tasks are carefully designed to be solvable without specialized exploration. Nevertheless, our investigation finds that standard RL methods often neglect long-term effects due to discounting, while general-purpose hierarchical RL approaches struggle unless additional abstract domain knowledge can be exploited.

• LTL2Action: Generalizing LTL Instructions for Multi-Task RL   (ICML 2021)

  by Pashootan Vaezipoor*, Andrew Li*, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Talk   Poster   Blog Post   Code

  Abstract: We address the problem of teaching a deep reinforcement learning (RL) agent to follow instructions in multi-task environments. Instructions are expressed in a well-known formal language – linear temporal logic (LTL) – and can specify a diversity of complex, temporally extended behaviours, including conditionals and alternative realizations. Our proposed learning approach exploits the compositional syntax and the semantics of LTL, enabling our RL agent to learn task-conditioned policies that generalize to new instructions, not observed during training. To reduce the overhead of learning LTL semantics, we introduce an environment-agnostic LTL pretraining scheme which improves sample-efficiency in downstream environments. Experiments on discrete and continuous domains target combinatorial task sets of up to ∼1039 unique tasks and demonstrate the strength of our approach in learning to solve (unseen) tasks, given LTL instructions.

• Interpretable Sequence Classification via Discrete Optimization   (AAAI 2021)

  by Maayan Shvo, Andrew Li, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Appendix   Talk   Poster   Code

  Abstract: Sequence classification is the task of predicting a class label given a sequence of observations. In many applications such as healthcare monitoring or intrusion detection, early classification is crucial to prompt intervention. In this work, we learn sequence classifiers that favour early classification from an evolving observation trace. While many state-of-the-art sequence classifiers are neural networks, and in particular LSTMs, our classifiers take the form of finite state automata and are learned via discrete optimization. Our automata-based classifiers are interpretable—supporting explanation, counterfactual reasoning, and human-in-the-loop modification—and have strong empirical performance. Experiments over a suite of goal recognition and behaviour classification datasets show our learned automata-based classifiers to have comparable test performance to LSTM-based classifiers, with the added advantage of being interpretable.

• Learning Symbolic Representations for Reinforcement Learning of Non-Markovian Behavior   (KR2ML Workshop @ NeurIPS 2020)

  by Phillip Christofferson, Andrew Li, Rodrigo Toro Icarte, Sheila McIlraith
  Paper   Poster

  Abstract: Many real-world reinforcement learning (RL) problems necessitate learning complex, temporally extended behavior that may only receive reward signal when the behavior is completed. If the reward-worthy behavior is known, it can be specified in terms of a non-Markovian reward function—a function that depends on aspects of the state-action history, rather than just the current state and action. Such reward functions yield sparse rewards, necessitating an inordinate number of experiences to find a policy that captures the reward-worthy pattern of behavior. Recent work has leveraged Knowledge Representation (KR) to provide a symbolic abstraction of aspects of the state that summarize reward-relevant properties of the state-action history and support learning a Markovian decomposition of the problem in terms of an automaton over the KR. Providing such a decomposition has been shown to vastly improve learning rates, especially when coupled with algorithms that exploit automaton structure. Nevertheless, such techniques rely on a priori knowledge of the KR. In this work, we explore how to automatically discover useful state abstractions that support learning automata over the state-action history. The result is an end-to-end algorithm that can learn optimal policies with significantly fewer environment samples than state-of-the-art RL on simple non-Markovian domains.

• Bayesian Network Structure Learning with Side Constraints   (PGM 2018)

  by Andrew Li, Peter van Beek
  Paper   Poster   Code

  Abstract: Hybrid methods for Bayesian network structure learning that incorporate both observed data and expert knowledge have proven to be important in many fields. Previous studies have presented both exact and approximate hybrid methods for structure learning. In this paper, we propose an approximate method based on local search that is capable of efficiently handling a variety of prior knowledge constraints, including an important class of non-decomposable ancestral constraints that assert indirect causation between random variables. In our experiments, our proposed approximate method is able to significantly outperform an existing state-of-the-art approximate method in finding feasible solutions when hard constraints are imposed. Our approach is able to find nearoptimal networks while scaling up to almost fifty random variables. In contrast, previous exact methods are unable to handle more than twenty random variables. Furthermore, we show that when prior knowledge is integrated, we are often able to produce a network much closer to the ground truth network, particularly when the amount of data is limited.