Lecture 11: Formal Language Theory 3
2025-07-30
Recap
Regular Languages
The following are equivalent
\(A\) is regular
There is a DFA \(M\) such that \(L(M) = A\)
There is a NFA \(N\) such that \(L(N) = A\)
Closure
If \(A\), \(B\) are regular, so are
\(\overline{A}\)
\(A \cup B\)
\(A \cap B\)
\(AB\)
\(A^n\)
\(A^*\)
Regular Expressions
Let \(\Sigma\) be an alphabet. Define the set of regular expressions \(\mathcal{R}_\Sigma\) recursively as follows.
\(\mathcal{R}_\Sigma\) is the smallest set such that
\(\emptyset \in \mathcal{R}_\Sigma\)
\(\epsilon\in \mathcal{R}_\Sigma\)
\(a \in \mathcal{R}_\Sigma\) for each \(a \in \Sigma\)
\(R \in \mathcal{R}_\Sigma \implies (R)^* \in \mathcal{R}_\Sigma\)
\(R_1, R_2 \in \mathcal{R}_\Sigma \implies (R_1R_2) \in \mathcal{R}_\Sigma\)
\(R_1, R_2 \in \mathcal{R}_\Sigma \implies (R_1 | R_2) \in \mathcal{R}_\Sigma\)
Language of a Regular Expression
The language if a regular expression \(R\), denoted \(L(R)\) is the set of strings that \(R\) matches. Formally,
\(L(\emptyset) = \emptyset\)
\(L(\epsilon) = \{\epsilon\}\)
\(L(a) = \{a\}\), for \(a \in \Sigma\)
\(L(R^*) = L(R)^*\) for \(R \in \mathcal{R}_\Sigma^*\)
\(L(R_1R_2) = L(R_1)L(R_2)\) for \(R_1, R_2\in \mathcal{R}_\Sigma\)
\(L(R_1 | R_2) = L(R_1) \cup L(R_2)\) for \(R_1, R_2\in \mathcal{R}_\Sigma\)
Equivalence of NFAs and Regular Expressions (!)
Equivalence of NFAs and Regex
For every regular expression \(R\), there exists a NFA \(N\) such that \(L(R) = L(N)\).
Regex \(\to\) NFA
We want to show \(\forall R \in \mathcal{R}_\Sigma\), there is an equivalent NFA. How do we do this?
Solution
By structural induction!Regex \(\to\) NFA
Solution
Base cases.
\(\emptyset\) has an equivalent NFA - one without an accept state!
\(\epsilon\) has an equivalent NFA - one with just an accept state!
For each \(a \in \Sigma\), \(a\) has an equivalent NFA - the following:
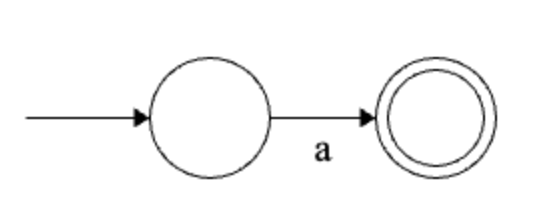
Inductive step. Suppose \(R, S \in \mathcal{R}_\Sigma\), and have equivalent NFAs \(M\), and \(N\). We need to show that \(R|S, RS, R^*\) all have equivalent NFAs.
\(R|S\). \(L(R|S) = L(R) \cup L(S)\). By the inductive hypothesis, this is then equal to \(L(M) \cup L(N)\). Since \(L(M)\) and \(L(N)\) are the languages of NFAs, they are regular. Since regular languages are closed under \(\cup\) (from last lecture), \(L(M) \cup L(N)\) is regular and hence has some NFA \(N'\).
\(RS\). This follows from an identical argument as above, using the observation that regular languages are closed under concatenation.
\(R^*\). This follows from an identical argument as above, using the observation that regular languages are closed under \({}^*\).
NFA to Regex
Example 1
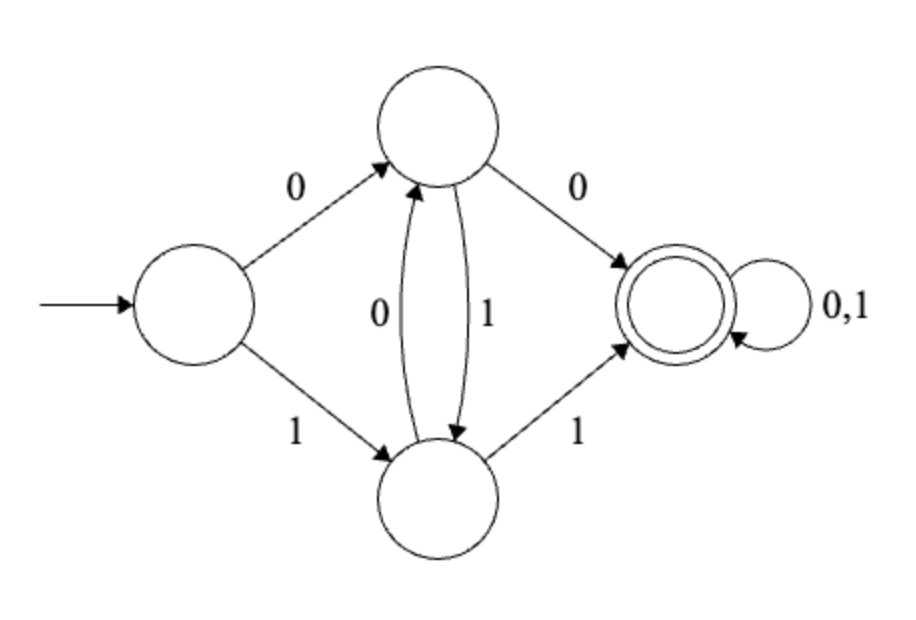
Solution
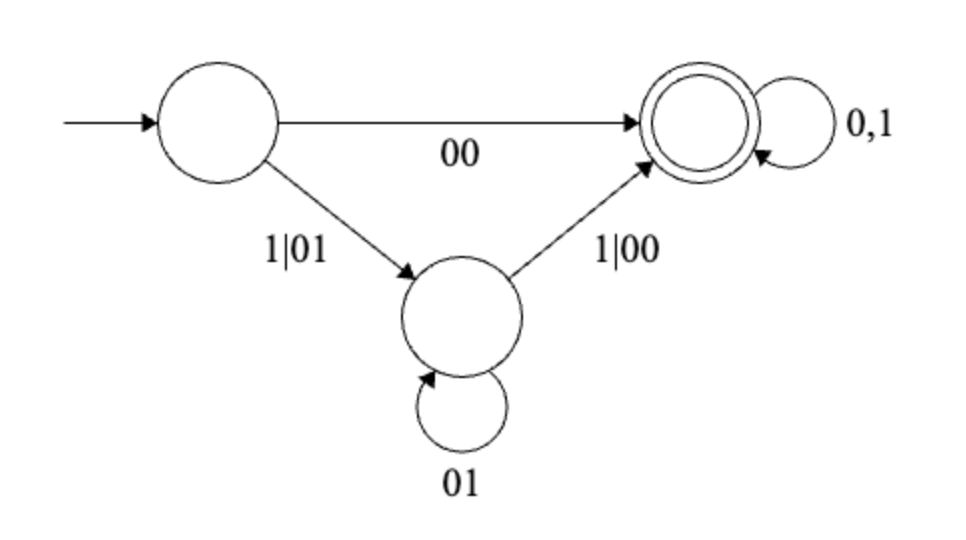
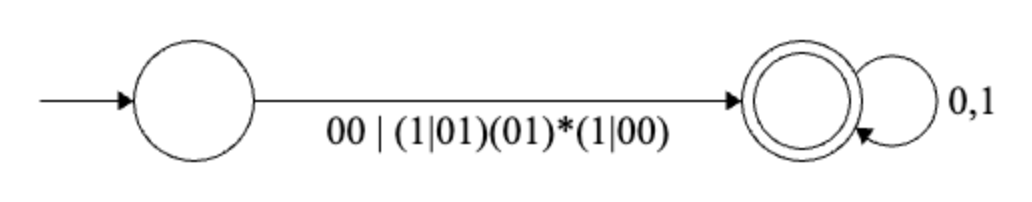
Final regular expression: \[ (00|(1|01)(01)^*(1|00))(0|1)^* \]
Example 2
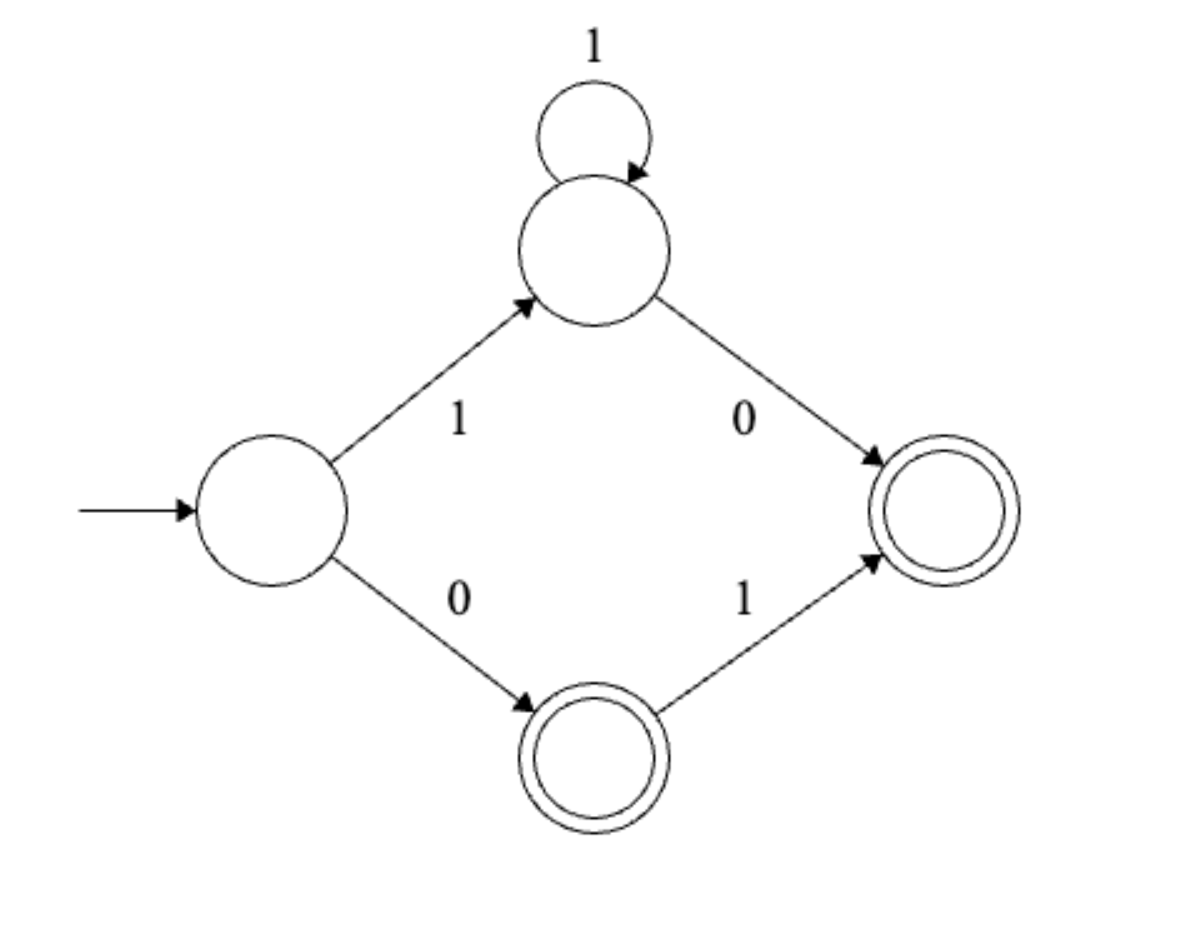
Solution
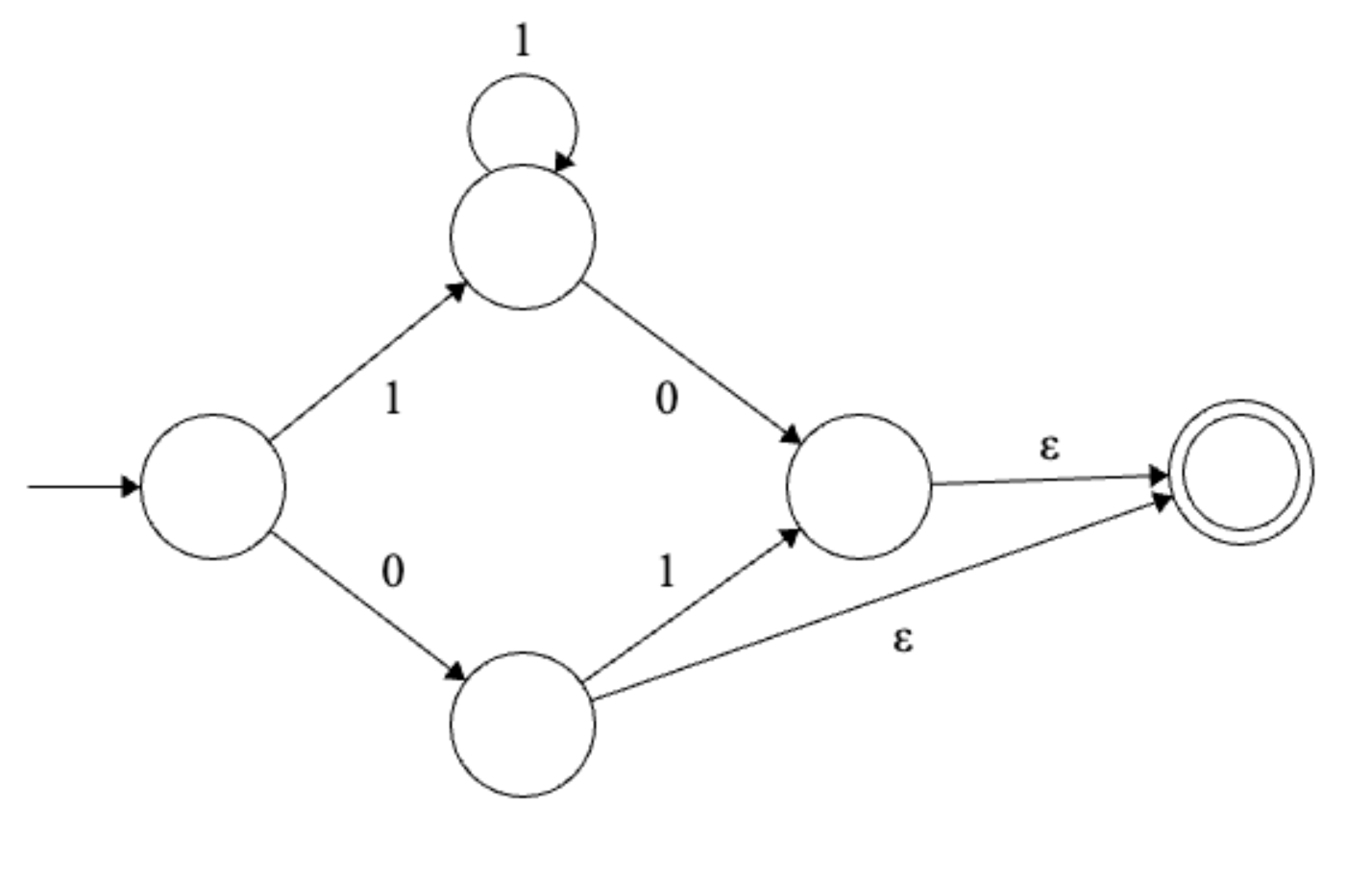
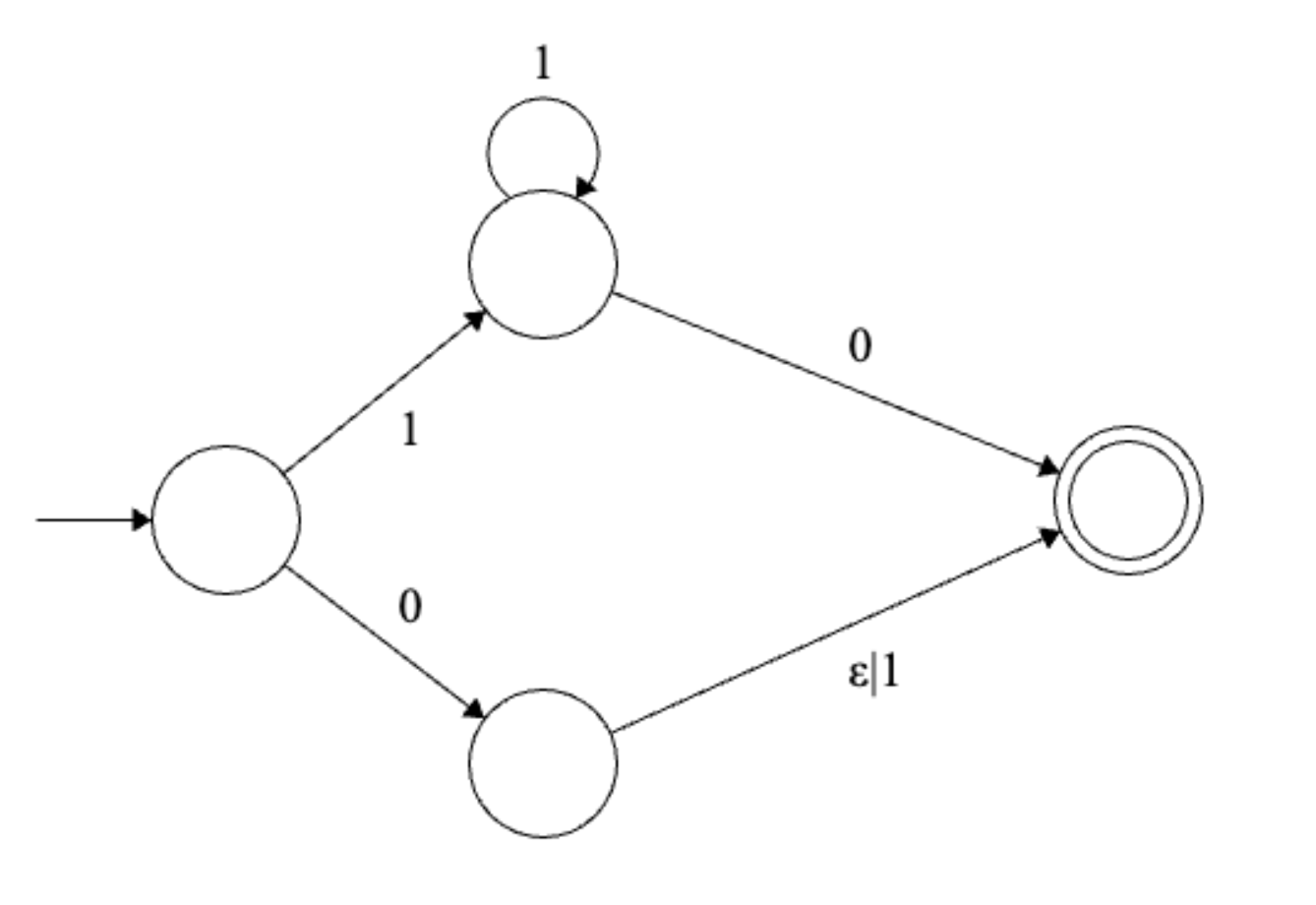
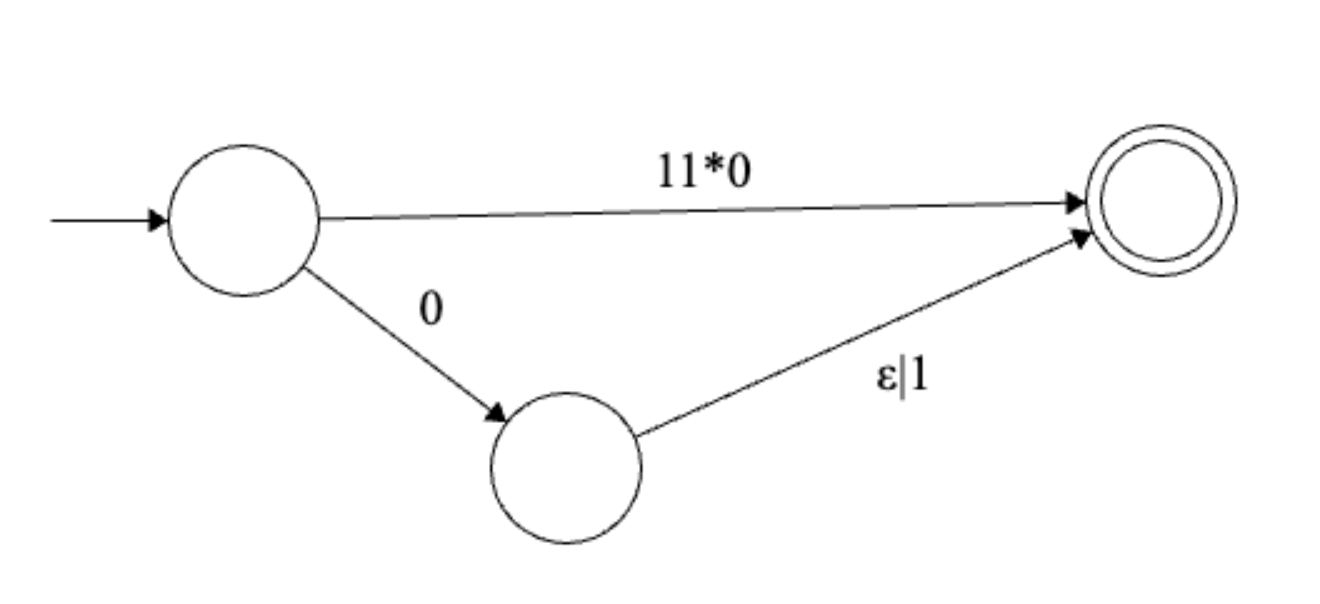
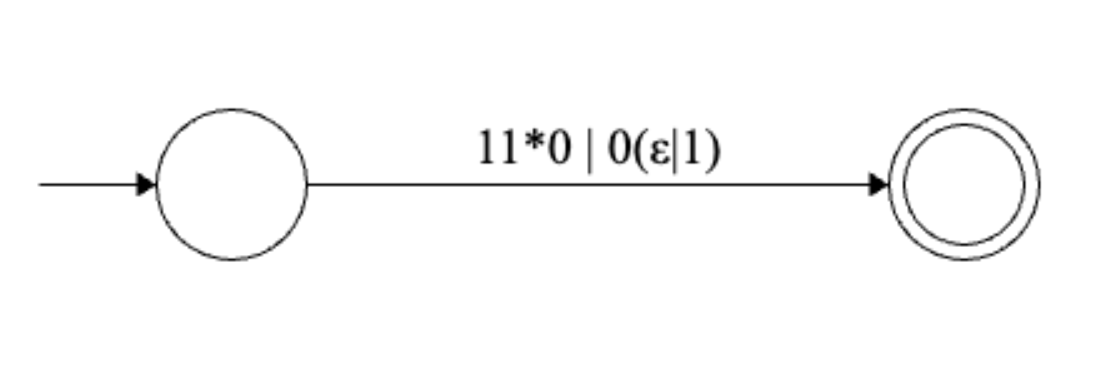 Final regular expression: \(1^+0 | 0(\epsilon | 1)\)
Final regular expression: \(1^+0 | 0(\epsilon | 1)\)
Sketch
Alter the NFA so there’s just one accepting state (using \(\epsilon\) transitions).
Iteratively rip out states, replacing transitions with regular expressions until you have something that looks like
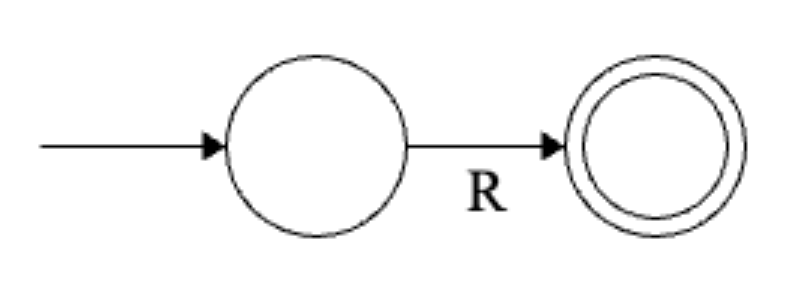
\(R\) is the equivalent regular expression.
“Ripping” out states
For two states \(q_1, q_2\) with a transition between them, let \(f(q_1, q_2)\) be the regular expression labelling the transition.
Here are the steps to rip out a state \(q\).
Remove the loop: If there is a self loop on state \(q\), for each state \(s\) with a transition into \(q\), update the transition \(f(s, q) = f(s, q)f(q,q)^*\). For each state \(s'\) with a transition out of \(q\), update the transition \(f(q, s') = f(q,q)^*f(q, s')\)
Bypass \(q\): for each path \((s, q, t)\) of length \(2\) through \(q\), update \(f(s, t) = f(s, t) | f(s, q)f(q, t)\). Note that it is possible that \(s = t\), in which case this step adds a loop.
Remove \(q\).
Regular Languages
The following are equivalent
\(A\) is regular
There is a DFA \(M\) such that \(L(M) = A\)
There is a NFA \(N\) such that \(L(N) = A\)
There is a regular expression \(R\) such that \(L(R) = A\)
Consequences
If I ask you to show me a language \(A\) is regular, you can choose to give me either a DFA, NFA or a regular expression!
How to choose
I typically use regular expressions for languages that seem to require some form of ‘matching’. For example contains 121 as a substring, or ends with 11. Regular expressions are typically faster to find and write out in an exam setting.
I’ll use NFAs when I can’t easily figure out a regular expression for something. These are usually languages for which memory seems to be useful like the \(\mathrm{Dogwalk}\) example from hw.
Stuff involving negations also seems easier to do with NFAs than with regular expressions. For example, contains the substring \(011\) is easy with regular expression, but doesn’t contain the substring \(011\) is a bit more complicated.
Non-regular Languages
We showed a bunch of languages were regular...
However, from lecture 1, we know that there are some problems that computers can’t solve...
... so what do non-regular languages look like?
What are some limitations for DFAs and NFAs?
Regular languages KEY intuition
DFAs has a finite number of states.
States correspond to memory.
Thus, DFAs can compute languages that only need a finite amount of memory (and read the input once left to right).
In particular, a DFA has a fixed amount of memory, no matter how large the input is.
Example
\(\mathbf{Even}\) is regular because no matter how large the input is, I only need to store one bit corresponding to whether or not the input has an even number of \(1\)s so far.
Infinite Memory Required
What are some things you can’t do with a fixed amount of memory?
Solution
Even simple things like storing the length of the input or the number of 1s - we don’t know in advance how long our input string can be!Example
Here’s an example of a language that can’t be computed using finite memory.
\[ \{a^nb^n: n \in \mathbb{N}\} \]
Why?
I don’t know ahead of time how many \(a\)s there are, and I need to keep track of them to see how many \(b\)s I should expect.
Proving not regular
Intuitively, \[ X = \{a^nb^n: n \in \mathbb{N}\} \]
requires infinite memory so is not regular.
To show \(X\) is not regular, we need to show that there does not exist a DFA \(M\) such that \(L(M) = X\).
\(X = \{a^nb^n: n \in \mathbb{N}\}\) is not regular
Solution
By contradiction, suppose there was a DFA \(M\) such that \(L(M) = X\).
Claim: Suppose \(m, n \in \mathbb{N}\) such that \(m \neq n\), then \(M\) run on \(a^m\) and \(a^n\) end up in different states.
Proof of claim. Let \(q_m\), \(q_n\) be the states reached after reading \(a^m\) and \(a^n\) respectively. By contradiction, suppose \(q_m = q_n\). Suppose from this state, we then read \(b^m\), let \(q'\) be the final state. Since \(a^mb^m \in X\), \(q'\) should be accepting. However, since \(a^nb^m \notin X\), \(q'\) should be rejecting, we have reached a contradiction since \(q'\) cannot be both.
By the claim, the DFA must reach a unique state for each \(a, aa, aaa,...\). Thus, \(M\) must have infinitely many states, which is a contradiction since \(M\) is supposed to be a DFA.Key Insights
Same state \(\implies\) same fate. If two strings \(x, y\) led the DFA to the same state. No matter what string \(w\) was read after, either \(xw\) and \(yw\) both get accepted or \(yw\) both get rejected.
The language \(\{a^nb^n: n \in \mathbb{N}\}\) had infinitely many strings that do NOT share the same fate (and hence must have distinct states).
“Same state same fate” but more formal
Let \(A\) be any language and \(x, y \in \Sigma^*\). Call \(x\) and \(y\) distinguishable relative to \(A\) if there exists \(w\) such that one of \(xw\) and \(yw\) are in \(A\) and the other is not. If \(x\) and \(y\) are not distinguishable, call them indistinguishable relative to \(A\)1.
Same state same fate. Suppose \(M\) is a DFA such that \(L(M) = A\), and let \(q_x\) and \(q_y\) be the states reached after reading \(x\) and \(y\), respectively. If \(q_x = q_y\), then \(x\) and \(y\) are indistinguishable relative to \(A\).
Proof (informal)
Solution
Essentially, the DFA is deterministic, depending only on the current state and the character read.Myhill-Nerode Theorem
Myhill-Nerode Theorem (corollary)
Let \(A\) be a language over \(\Sigma\). Suppose there exists a set \(S \subseteq\Sigma^*\) with the following properties
(Infinite). \(S\) is infinite
(Pairwise distinguishable). \(\forall x, y \in S\), with \(x \neq y\). \(x\), and \(y\) are distinguishable relative to \(A\).
Then \(A\) is not regular.
Proof
Solution
Let \(A\) be language, and suppose \(S \subseteq\Sigma^*\) is infinite and pairwise distinguishable relative to \(A\). WTS \(A\) is not regular.
By contradiction, suppose \(A\) was regular, then there exists some DFA \(M\) such that \(L(M) = A\). Since \(M\) is a DFA, it has some finite set of states \(Q\).
Let \(g: S \to Q\), be a function mapping strings \(x \in S\) to the state the DFA reaches after reading \(x\) from the start state.
Since \(S\) is infinite, and \(Q\) is finite, \(g\) is not injective. Therefore, there exist two strings \(x, y \in S\) such that \(g(x) = g(y)\). That is \(x\) and \(y\) reach the same state. Since \(x\) and \(y\) are in \(S\), they are distinguishable; however, by the lemma, they are indistinguishable, which is a contradiction.Using The Myhill-Nerode Theorem
To show a \(A\) is not regular, it suffices (by the Myhill-Nerode Theorem) to find a set of strings, \(S\), such that \(S\) is infinite and pairwise distinguishable relative to \(A\).
Proof: \(X = \{a^nb^n: n \in \mathbb{N}\}\) is not regular
Solution
Consider the set \(S = \{a^n: n \in \mathbb{N}\}\) and note that \(S\) is infinite since it has one element for every natural number.
Let \(x, y \in S\) with \(x \neq y\). Then \(x = a^i\), \(y = a^j\) for some \(i \neq j\). We’ll show that \(x \not \sim y\), in particular, \(w = b^i\) is such that \(xw = a^ib^i \in X\), but \(yw = a^jb^i \notin X\). Thus, \(S\) is an infinite set of pairwise distinguishable strings relative to \(X\), so \(X\) is not regular.A note about the pumping lemma
The pumping lemma is an alternate way to show that a language is not regular.
I used to cover both the pumping lemma and the Myhill-Nerode theorem in class, but I found that students found the Myhill-Nerode theorem easier to understand and use.
You do not need to know the pumping lemma for this course, but if you’re interested, there is a chapter in Sipser that covers it.
CSC236 Summer 2025