A subtle point is that ![]() describes the distribution we want, but
it doesn't directly help create it. Programming languages often
provide a way of generating a sequence of pseudo-random integers in
the range
describes the distribution we want, but
it doesn't directly help create it. Programming languages often
provide a way of generating a sequence of pseudo-random integers in
the range ![]() by starting at some integer
by starting at some integer ![]() and then
continuing using the relation:
and then
continuing using the relation:
We need a way to associate each number we generate in ![]() with a
number in our desired distribution. The first step is to construct
the cumulative distribution function
with a
number in our desired distribution. The first step is to construct
the cumulative distribution function ![]() which represents the
probability that
which represents the
probability that ![]() :
:
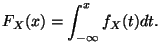
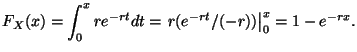
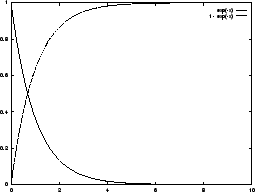
Now we can invert ![]() -- turn the graph sideways! For
each
-- turn the graph sideways! For
each
![]() we generate, we can solve
we generate, we can solve
![]() in
order to find the corresponding
in
order to find the corresponding ![]() . Rearrange the equation and take
. Rearrange the equation and take
![]() (natural log) of both sides, and you have
(natural log) of both sides, and you have
![]() . We
don't have to worry about taking
. We
don't have to worry about taking ![]() , since we rigged things so
that
, since we rigged things so
that ![]() is never 1.
A more straight-forward task is to invert a uniform continuous
distribution on the interval
is never 1.
A more straight-forward task is to invert a uniform continuous
distribution on the interval ![]() . If
. If
![]() the cumulative
distribution is
the cumulative
distribution is ![]() =
=
![]() , so now we solve for
, so now we solve for
![]() , or
, or
![]() .
.