


Next: Discrete distributions
Up: November lecture summary
Previous: Barber simulation
October 8
In many simulations we want a value to be calculated ``randomly,''
that is chosen from some distribution of values where each
particularly choice is unknowable in advance. Since we're simulating
this on a computer where there has to be some rule for
calculating the values, we usually use a pseudo-random sequence of
values that obey our desired distribution of values, and instead of
``unknowable'' we settle for hard-to-know in advance.
Some of the distributions we simulate are
- uniform:
- Each value in some range has an equal chance of
occurring (for example we expect each number on a single fair die to
occur in 1/6 of the rolls)
- normal:
- Two or more independent events are summed (e.g. two
dice), yielding a familiar bell-shaped curve.
- exponential:
- The range of values is infinite, but we determine
in advance what the mean (average) value is. Streetcars may arrive every
10 minutes on average, but this includes cases where five arrive
bunched together plus the cases when equipment failure suspends
service for several hours.
As well as these distributions we distinguish discrete
distributions (there is a finite set of possible values), and
continuous distributions (infinitely many values along some
segment of the real line).
We describe probability that a value, or range of values, will occur
by inventing a random variable 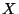 , a probability density function
, a probability density function
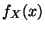 indicating the likelihood that
indicating the likelihood that 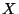 will be
will be 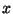 (note the
upper/lower case distinction), setting
(note the
upper/lower case distinction), setting 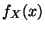 to some value in
to some value in
![$ [0,1]$](img198.gif) , and insisting that the sum of
, and insisting that the sum of 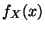 for all
for all 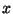 is 1. If
is 1. If
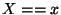 is impossible, then
is impossible, then 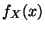 is zero. If
is zero. If 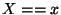 is
certain, then
is
certain, then 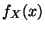 is 1. Most cases are between these extremes.
is 1. Most cases are between these extremes.
Subsections



Next: Discrete distributions
Up: November lecture summary
Previous: Barber simulation
Danny Heap
2002-12-16
![]() , a probability density function
, a probability density function
![]() indicating the likelihood that
indicating the likelihood that ![]() will be
will be ![]() (note the
upper/lower case distinction), setting
(note the
upper/lower case distinction), setting ![]() to some value in
to some value in
![]() , and insisting that the sum of
, and insisting that the sum of ![]() for all
for all ![]() is 1. If
is 1. If
![]() is impossible, then
is impossible, then ![]() is zero. If
is zero. If ![]() is
certain, then
is
certain, then ![]() is 1. Most cases are between these extremes.
is 1. Most cases are between these extremes.