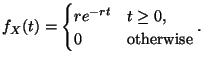Things are slightly less intuitive when our event can be selected from a segment of points on the real line. For example, I usually tell anyone who cares that I'm 166 centimeters tall. However, I'm sure that a precise enough measure would determine that I'm not exactly 166.000000...cm tall. Adult human heights are distributed over some interval between 1 meter and 3 meters (to be generous), but the chance that some particular exact height is achieved is basically zero.
So we change our point of view and talk about the probability that our
value falls within some particular range. We define ![]() so that
its values are always non-negative and its integral from
so that
its values are always non-negative and its integral from ![]() to
to ![]() represents the probability that
represents the probability that ![]() takes a value in
takes a value in ![]() :
:
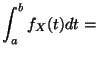 probability that
probability that ![$\displaystyle f_X(x) =
\begin{cases}
1/(b-a) & x \in [a,b] \\
0 & \text{otherwise}
\end{cases}$](img212.gif)