


Next: Your job
Up: Approximating iteratively: CSC270, Assignment
Previous: A warm-up function
A more challenging function
In the previous section, you may have wondered ``why bother with an
iterative solution when I can easily see that 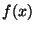
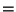
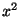 is a
solution?'' However, what if you were modelling a problem where
things were a bit messier? Suppose you knew that for some constant
is a
solution?'' However, what if you were modelling a problem where
things were a bit messier? Suppose you knew that for some constant
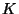 you had:
you had:
Once again you have an unknown function, 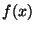 , defined in terms of
its derivative.1However, our current definition is more complicated, since the
right-hand side is an expression in both
, defined in terms of
its derivative.1However, our current definition is more complicated, since the
right-hand side is an expression in both 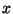 and our unknown function
and our unknown function
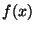 . You might have studied differential equations (which
Equation 1 is) and be able to use a well-studied bag of
tricks (integrals, integrating factors, etc.)2to work out with paper and pencil that
. You might have studied differential equations (which
Equation 1 is) and be able to use a well-studied bag of
tricks (integrals, integrating factors, etc.)2to work out with paper and pencil that
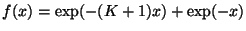 |
(3) |
However, if what you need is an approximation, you can proceed as in
the previous section:
- Decide on a step size that you'll increment
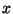 by (we used
0.1 in the last section, but your mileage may vary), and call it
by (we used
0.1 in the last section, but your mileage may vary), and call it
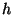 .
.
- Denote your approximate function as
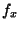 to distinguish it
from the exact function
to distinguish it
from the exact function 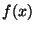 . Also denote the approximate
derivative as
. Also denote the approximate
derivative as 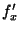 , since it won't always be identical to
, since it won't always be identical to
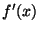 .
.
- Since you are given the exact value
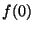
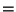 2, start things
out on the right foot by setting
2, start things
out on the right foot by setting 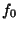
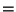 2, and the initial value of
2, and the initial value of
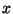
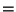 0.
0.
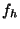 is
is
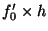

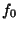 , and
, and 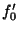 is
calculated by by substituting
is
calculated by by substituting 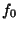 for
for 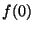 in
Equation 1.
in
Equation 1.
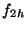 is
is
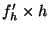

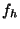 , substituting
, substituting 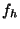 for
for 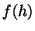 in
Equation 1.
in
Equation 1.
- And so on...
Since you've been given the exact expression for 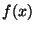 , you can
always compare your approximation
, you can
always compare your approximation 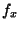 to
to 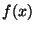 .
.



Next: Your job
Up: Approximating iteratively: CSC270, Assignment
Previous: A warm-up function
Danny Heap
2002-09-22
![]()
![]()
![]() is a
solution?'' However, what if you were modelling a problem where
things were a bit messier? Suppose you knew that for some constant
is a
solution?'' However, what if you were modelling a problem where
things were a bit messier? Suppose you knew that for some constant
![]() you had:
you had: