A warm-up function

Suppose you're building a reflector to concentrate the sun's rays. After a bit of thought you conclude that the reflector should be circular when viewed from above, and that its cross-section in any vertical plane should always have a slope equal to twice its distance from the reflector's centre. You've got a knack for mathematical notation, so you say that if the distance from the centre is called $x$, then your reflector should have vertical cross-sections that correspond to a function $f(x)$ with derivative $2x$. How do you find the function $f(x)$ that satisfies $f'(x)$ $=$ $2x$?

Since you've recently studied some calculus, you might recognize that $f(x)$ $=$ $x^2$ will work (as will $f(x)$ $=$ $x^2 + 37$, and many other similar functions). Or you might haul out the Fundamental Theorem of Calculus and integrate both sides of $f'(x)$ $=$ $2x$ to come up with the same result. Or you might decide to use the following iterative approximation:

Figure: The variable $x$ is incremented by $0.1$ at each step. Use the known value of $f(x)$ at the initial point, $x=0$), and then use the approximation $f_x$ $=$ $f'(x-0.1)$ $\times$ $0.1$ $+$ $f_{x-0.1}$.

$x$	$f_x$	$f(x)$	$x$	$f_x$	$f(x)$
0.0	0.0	0.0	0.6	0.3	0.36
0.1	0.0	0.01	0.7	0.42	0.49
0.2	0.02	0.04	0.8	0.56	0.64
0.3	0.06	0.09	0.9	0.72	0.81
0.4	0.12	0.16	1.0	0.9	1.0
0.5	0.2	0.25	1.1	1.1	1.21

Since you can always place your reflector at ground level, you know that (at least) $f(0)$ $=$ 0 -- so you know at least one pair of coordinates $(0,f(0))$ $=$ $(0,0)$. Plugging this into your formula for $f'$, you can see that $f'(0)$ is also 0. You reason that you can approximate $f(h)$ (if $h$ is pretty small) by drawing the tangent line through $f(0)$ and then calling the point where this tangent line has horizontal component $h$ $(h,f_h)$ -- a pretty good approximation of $(h, f(h))$. In fact, you don't even need to draw the tangent line if you calculate $f_h$ $=$ $f(0)$ $+$ $f'(0)\times h$. You then iterate your approach -- you use your approximation $f_h \approx f(h)$ to calculate a new tangent, and with this you come up with a second approximation $(2h, f_{2h})$. If $h$ $=$ $0.1$, the result is shown in Figure 1.

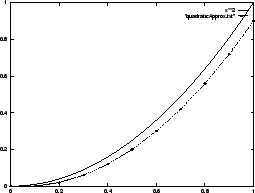
Clearly our approximate function (which we're denoting $f_x$ to distinguish it from $f(x)$) is not a perfect parabola. But it might turn out that if you build a reflector based on it, you'll be able to heat a can of soup. Otherwise, you'll need to think about how to improve your approximation.