Teaching

For a complete list of my teaching experience, see the home page. Here are some teaching materials I have developed over the years.

CSC236 (Introduction to the Theory of Computation)

Here are the course websites for when I taught the course in Summer 2023 and Summer 2025.

Notebooks + Coding Projects

For CSC373 (Algorithms, Design and Analysis)

These notebooks accompany the undergraduate algorithms course at U of T. I developed them when I taught the course in 2024.

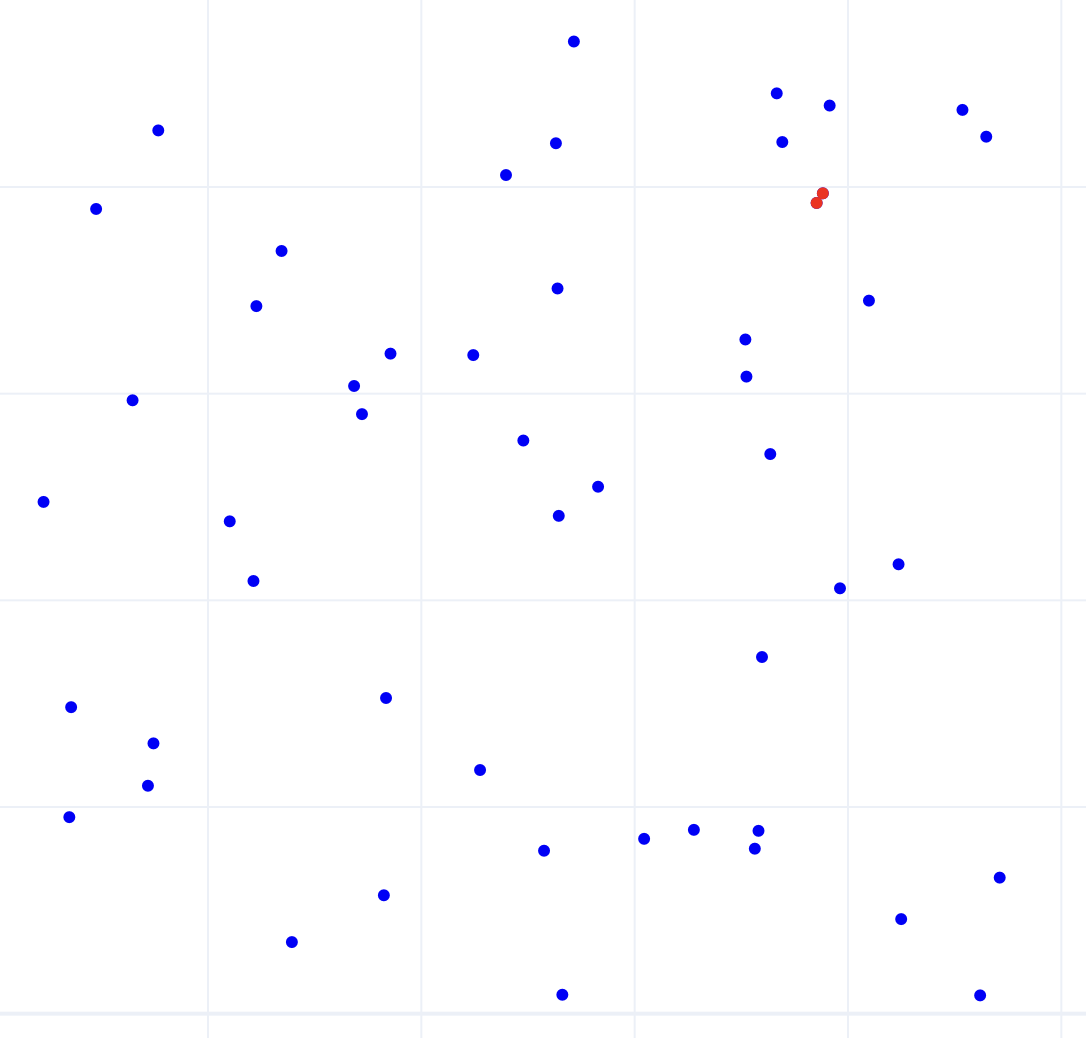
  • Huffman Coding and Closest Pair in \(\mathbb{R}^2\)

    • In this notebook, students implement two algorithms from class: Huffman Coding and the Closest pair in \(\mathbb{R}^2\)
    • There are visualizations for both algorithms
    • For the closest pair in \(\mathbb{R}^2\) problem, there is a runtime comparison with the naive algorithm.

  • Dynamic Programming

    • In this notebook, students implement DP algorithms for the knapsack problem and the traveling salesman problem.
    • Students who completed the Journey through Hoenn notebook in 236 will now be able to find an exact solution (instead of an approximate one)!

  • Flow and LP

    • In this notebook, students model and solve matchmaking problem - matching CS students with business students for a group project.
    • The unweighted version (maximum cardinality matching) is solved via max flow
    • The weighted version is solved via LP
    • Python libraries networkx and scipy are used to solve max flow and linear programming respectively.

For CSC236 (Introduction to the Theory of Computation)

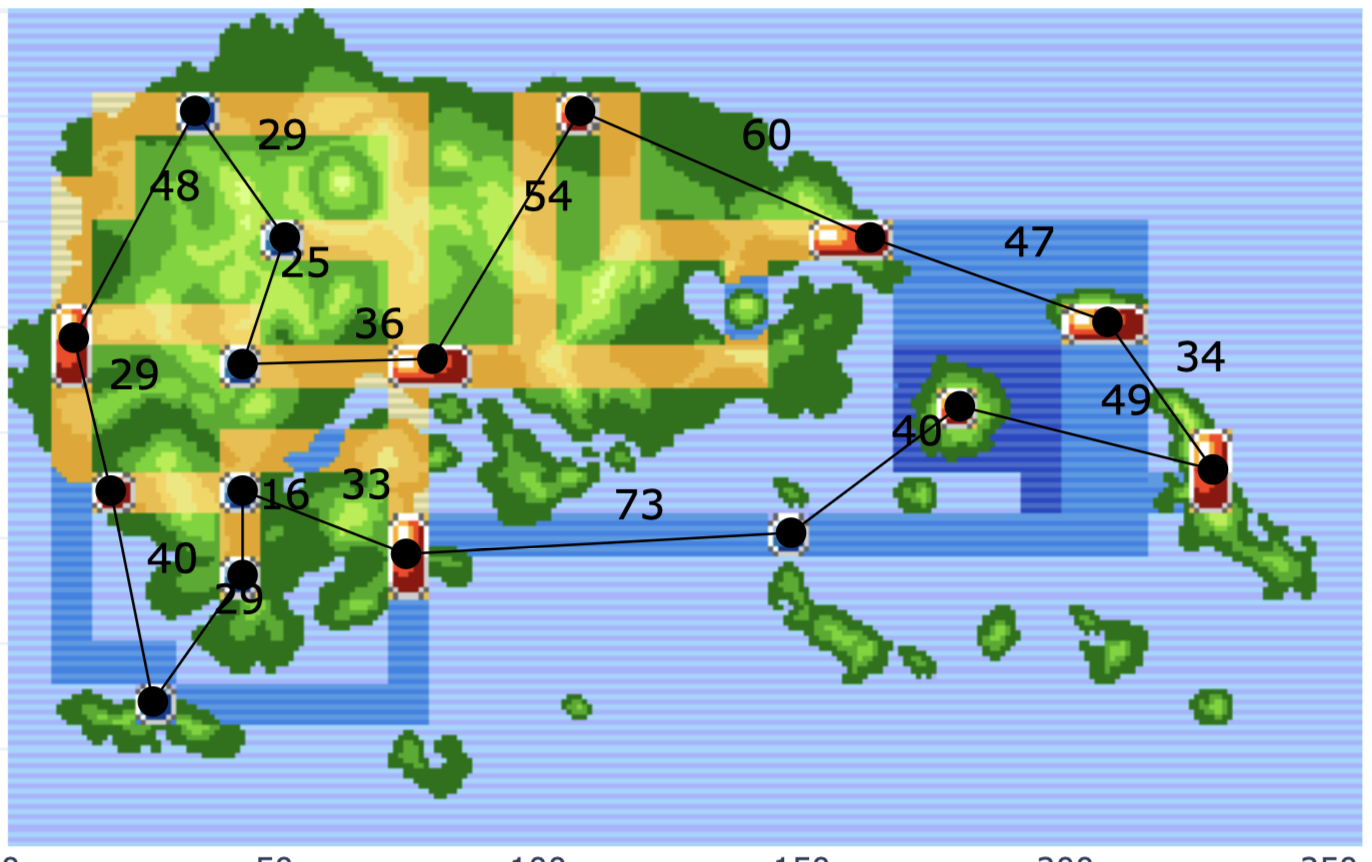
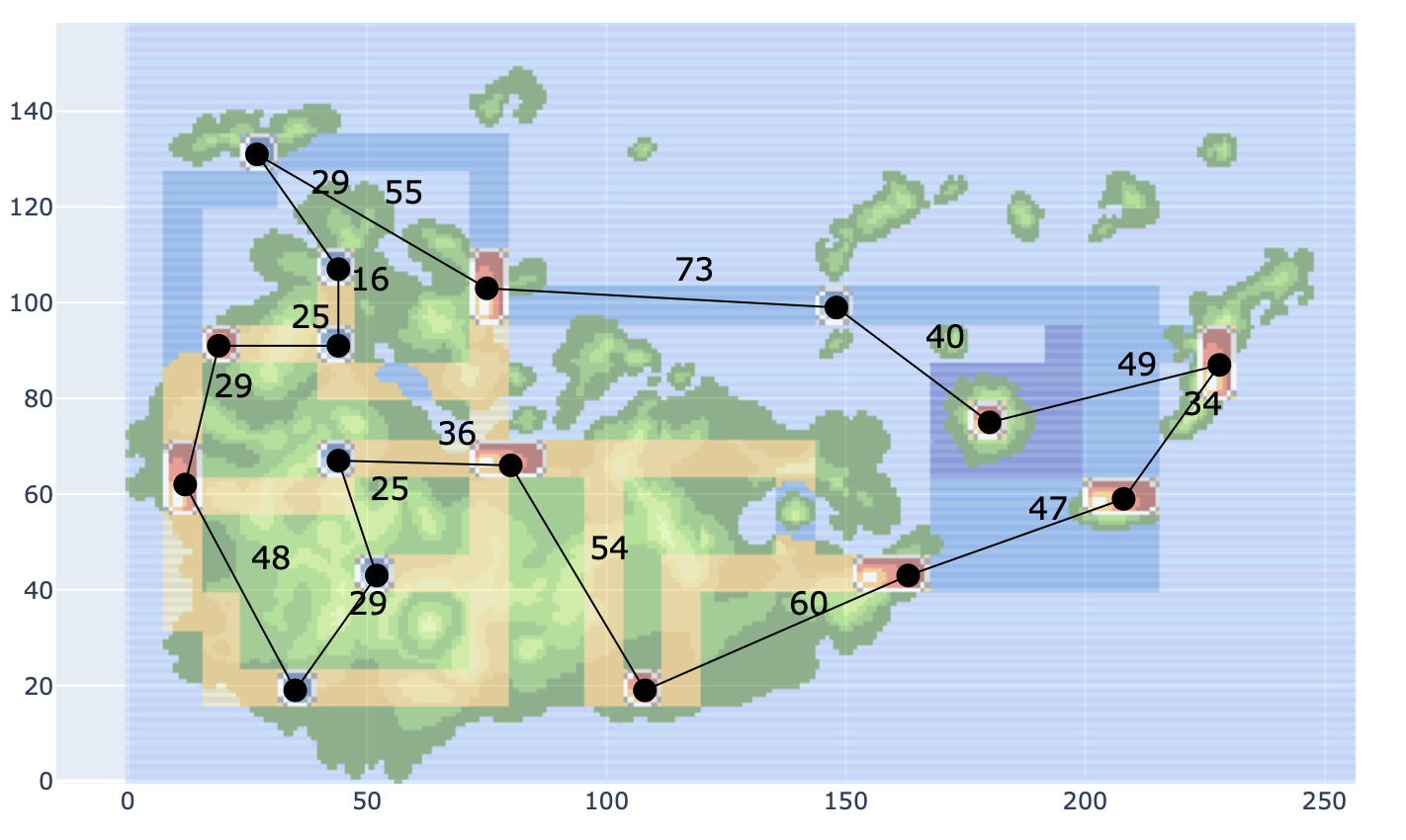
  • A Journey Through Hoenn
    • In this notebook, students model the problem of finding the quickest way to visit each city in the City of Hoenn (from Pokemon Emerald) as a graph problem and approximate a solution using the networkx library
    • There are variants for where you can move in any direction and where you can move only up/down/left/right.
    • As a bonus, the notebook explores a relaxation of the problem where backtracking is free. I.e. If I have visited a city before, I can fly to it again at zero cost. This variant can then be modeled by another well-known graph problem.

For Inspirit AI

These are notebooks I developed for Inspirit AI. These projects are for students at the high school and middle school levels.

  • Self driving cars: 1, 2, 3

    • In this project, students gradually build models to drive cars in one of the OpenAI Gyms environments.
    • The project starts with basic models to decide whether the road turns left or right and gradually builds to models based on behavioral cloning and deep Q-learning.

  • Covid mask detection: 1, 2, 3

    • In this project, students build models to detect whether or not someone is wearing a mask.
    • The models start very simple (using the color distribution of the input image) and gradually get more complex, building up to a convolutional neural network with a facial recognition preprocessing step.
    • Students then get a chance to test the model on their images.

  • Game playing AI - the minimax algorithm and variants

    • Students implement the minimax algorithm and use it to play tic-tac-toe and connect 4.
    • Students tune a heuristic evaluation function and then get to play against their algorithm, which is always fun :)