Numerical integration (aka quadrature)

From a user's perspective, integral calculus has a strange paradox. You're told that for any continuous function, the area under its graph (roughly its integral) exists. However, there is an exact paper-and-pencil method for finding integrals only for a tiny minority of continuous functions, and a large part of the art of calculus consists of guessing which of the various methods (integration by parts, substitution, partial fractions, ...) will work on a particular function. This sort of thing is difficult (probably impossible) to specify in an algorithm for a computer, so we use numerical methods to find a number sufficiently close to a definite integral.

The idea is to divide up the $x$ values our function $f(x)$ is defined on into a group of intervals. Over each interval, we make an estimate of our function whose integral we already know. As we partition into smaller and smaller intervals, we get closer approximations of our desired integral.

If a typical subinterval is $[a,b]$, then the simplest approximation of the area under the graph is the rectangle with base of length $b-a$ and height of $f$ at the midpoint. This leads to the midpoint or rectangle rule:

$$I(f) \approx (b-a) \times f\left(\frac{a+b}{2}\right).$$

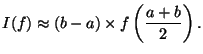
A better approximation of our function might be gained by drawing a line segment between $f(a)$ and $f(b)$, called the trapezoid rule:

$$I(f) \approx (b-a) \times \frac{f(a) + f(b)}{2}.$$

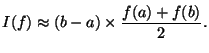
If the function might be well-approximated by a quadratic curve (parabola), then we use the two endpoints and the midpoint to determine a unique parabola, and use Simpson's rule:

$$I(f) \approx (b-a) \times \frac{f(a) + 4f([a+b]/2) + f(b)}{6}$$

Which rule to use means making judgements about the nature of the function being approximated, and are beyond the scope of this brief description.