


Next: Numerical integration (aka quadrature)
Up: October lecture summary
Previous: Newton's method
October 4
Newton's method used the first two terms of a function's Taylor
series, and omitted the others. Page 14 of the Course Notes provides
a formula for the error you can expect from this omission, called the
truncation error. If you omit all the terms from
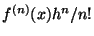 on, your error is:
on, your error is:
Although this formula doesn't tell us exactly what 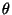 is, it
tells us its general neighbourhood. Often we can estimate the maximum
size that
is, it
tells us its general neighbourhood. Often we can estimate the maximum
size that
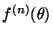 can be in the interval
can be in the interval ![$ [x,x+h]$](img108.gif) , and get
an idea of how bad our error can be. In the case of Newton's method,
this tells us that if
, and get
an idea of how bad our error can be. In the case of Newton's method,
this tells us that if 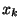 is distance
is distance 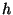 from the root, then
from the root, then
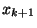 is some constant times
is some constant times 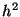 from the root -- quadratic
convergence.
from the root -- quadratic
convergence.
However, when 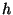 is big, you might not have convergence. You might
experiment with the innocent function
is big, you might not have convergence. You might
experiment with the innocent function
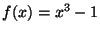 in the interval
in the interval
![$ [-2, 0]$](img114.gif) to find a couple of points where Newton's method fails to
converge.
to find a couple of points where Newton's method fails to
converge.
Subsections
Danny Heap
2002-12-16
![]() on, your error is:
on, your error is:
![]() is big, you might not have convergence. You might
experiment with the innocent function
is big, you might not have convergence. You might
experiment with the innocent function
![]() in the interval
in the interval
![]() to find a couple of points where Newton's method fails to
converge.
to find a couple of points where Newton's method fails to
converge.