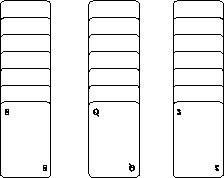
Figure 1: The layout of the cards.
Assignment 3: A Card Trick
Due: Thursday July 18, 6pm.
From the player's point of view, the trick proceeds as follows. The magician lays out 21 cards face up in 3 columns of 7 cards each (see figure 1). After choosing a card, the player indicates which column the card is in. The magician then gathers the cards up and lays them out again in the same pattern but in a different order. Once again the player indicates which column his chosen card is in, and the process is repeated once more. Then, the magician magically presents the card that the user chose.

Figure 1: The layout of the cards.
Here's how the trick is done. After the player indicates a column, the magician picks up each of the columns separately and places the chosen column in between the other two columns forming a deck of 21 cards. The cards are then laid out (for the second time) across columns, one card per column at a time (as in solitaire). After the player's second choice, they are picked up in the same manner as before, with the chosen column again sandwiched between the other two columns. Finally, after a third repetition, the chosen card always ends up as the middle card in the 21-card deck. Try it with a real deck of cards.
In this assignment, you will write a program that performs the trick. The computer will act as magician, and the user as player. The purpose of the assignment is to give you experience in using both linked lists and modules. The main work will be to design and implement a Turing module that stores and manipulates the current state of the cards involved in the trick. You will also have to write the main program that performs the trick by making calls to subprograms in the module.
There are obviously many ways to design and implement the module, so, for the sake of consistency (to help the markers), you must adhere to the following specification of the module.
There are 21 cards involved in the trick; at any time, they can be organized in one of two ways. Before being laid out, they are organized as a deck (i.e., a list) of cards. When the cards have been laid down for the user to view, they are organized as three lists of cards, one for each column. Notice that the data structure reflects the physical organization of the cards.
You are required to implement each list of cards as a linked list. Therefore, the 21-card deck will be a linked list, and each column will also be a separate linked list. Figure 2 shows the structure of the column layout. Note that The implementation of the list of columns is up to you. The whole implementation should be flexible enough to deal with other configurations, such as 4 columns of 4 cards, with only minor alterations.
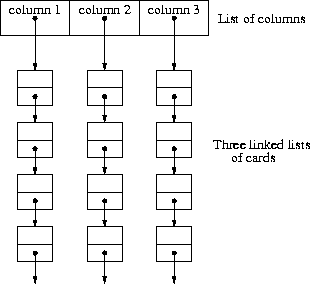
Figure 2: Structure of the column layout.
We also need a data type for a card. On the web page, we have provided a module called DeckOfCards, which defines and exports the following type:
type cardType :
record
suit : string (1) % "S", "H", "D", or "C"
value : string (2) % "A", "1" - "10", "J", "Q", "K"
end record
The DeckOfCards module is discussed in greater detail below.
Several operations are possible on this data structure; the following is a suggested breakdown. If you find a different set of operations to be better, then you may use it if you justify your decision in your report. Of course, you will probably want to further subdivide these operations into subprograms internal to the module.
The main program should import the module that you have written. At each stage of the trick it should ask the user to specify which column his chosen card is in. When the trick is complete it should tell the user which card he picked. If you want to be fancy, we have provided the Graphics module, which contains a subprogram called MouseLocation that returns the coordinates of the mouse when the button is pressed, so you could have the user select the column by using the mouse, instead of by typing.
You should write a short report that includes the following information. (Be clear, concise, and neat.)
We suggest that you first look over the two modules that we have provided. Observe their style, and use this style in your assignment. Also note how the DeckOfCards module makes use of the coord type defined in the Graphics module.
To learn how to use the modules, we suggest that you write a short main program that imports the modules, and displays all of the cards in the 52-card deck.
For the module that you are to write, start on paper by designing the data structures, and consider how to make the required operations on them as efficient as possible.
On the web page you will find:
1. The DeckOfCards module (be sure to save it as deck.t).
2. The Graphics module (be sure to save it as graphics.t).
This part is completely separate from the Part I, and requires only a written solution. It is meant to give you experience in analysing the differences and tradeoffs between different implementations of the same same abstract data type.
The problem: The Rhinoceros Party of Canada has hired you to write a program to help in their fund-raising. The program should store a list of members with information about their past contributions. The party membership changes often, but they don't have very many members on average, so you are able to store the entire list of members in memory. (Use of files is necessary only for backup purposes). The main purpose of the program is to generate mailing lists of different groups of members, for example, of members who have donated a lot in the past, or who have not paid fees in the current year.
The following information is stored for each member: surname, given names, street address, city or town name, province, postal code, date of last received membership fee, total donations, and amount of last donation.
You are considering four different implementations:
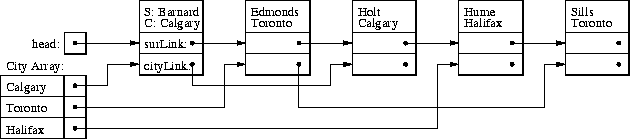
Figure 3: A list threaded on surname and city
Question: The following operations must be applied to the list of members. Discuss the relative merits of each implementation with respect to the amount of memory used by the structure, and the runtime used by each operation.
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -no_navigation as3.
The translation was initiated by Philip Edmonds on Tue Jun 25 12:13:57 EDT 1996