Non-Rigid Structure from Motion
Jump to Non-Rigid Motion: Introduction | Results | Publication, or Research Overview.
Introduction to Shape from Locally Rigid Motion.
A brief summary of our locally-rigid approach is available as a YouTube Video: Non-Rigid Structure by Locally-Rigid Motion. It shows the results obtained on two image sequences, and is worth viewing first to see the sort of motions that are being addressed. The introduction given below provides a more thorough description of the algorithm.
Suppose we are given an image sequence and we track a set of points (so the tracked points move with the image structure). Given these tracks we are interested in identifying differently moving objects and, if possible, estimating their 3D shapes. This is called the structure from motion problem.
 |
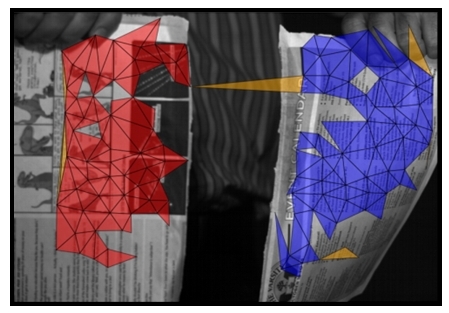
| One Frame of Tracked Points (in red) |
The structure from motion problem has been thoroughly studied in the literature for some types of scenes, namely scenes consisting of a single rigid object (equivalently, a stationary scene and a moving camera) or multiple rigid objects. However, recovering the 3D shape of non-rigid objects has recieved less attention.
Here we consider non-rigidly moving objects, such as the newspaper shown below, which is in the process of being torn in half. We would like to be able to recover the 3D shape and the change in the topology of the newspaper.
 |
| One Triangle of Tracked Points over Several Frames |
The key property we rely on is that the 3D motion is locally-rigid. That is, small triangles on the surface are essentially rigid in 3D. This approximation is valid if the surface does not stretch or bend significantly over most small triangles.
Given only image point tracks, our algorithm begins by considering many triples of tracks. It tests each triple for its consistency with a rigidly moving 3D triangle and, for consistent triples, the 3D lengths of the triangle edges are computed. This forms a soup of rigid 3D triangles.
|
A graph of triangles is formed by linking any pair of triangles which share an edge. This graph is then used to group triangles into components representing differently moving bodies.
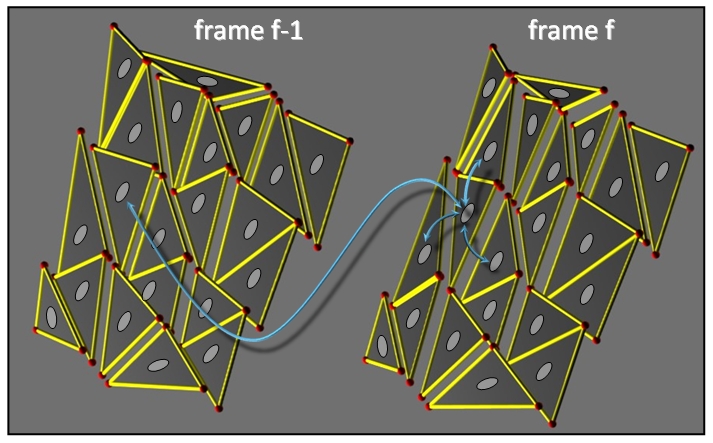 |
| Edges of MRF for Flips |
The 3D pose of each triangle in each frame is ambiguous up to a depth flip and a uniform translation in depth. To resolve the depth flips in each component we use a binary-valued, spatio-temporal, Markov random field (MRF) to represent an energy associated with each assignment of flips. The flips are determined by attempting to minimize this energy.
Once the depth flips of all the triangles in one component have been computed, we solve for each triangle's 3D depth relative to its neighbouring triangles. This gives the 3D depth of all the triangles in a component (in each frame), up to a uniform translation in depth.
 |
The three main steps of this overall process are shown above (where the viewpoint is from above, looking down on the various stages of the reconstruction process and one image of the sequence). For this sequence showing a newspaper being torn, the algorithm recovers two large connected groups of triangles, one on each side of the tear.

Jump to Non-Rigid Motion: Introduction | Results | Publication, or Research Overview.
Example Results.
The YouTube Video we mentioned above, Non-Rigid Structure by Locally-Rigid Motion, shows results of each step of this algorithm for two image sequences.
For the two sequences shown below, the image point tracks were kindly provided by Y. Tian and S. Narasimhan, using the algorithm described in their paper:
Y. Tian and S. Narasimhan, A globally optimal data-driven approach for image distortion estimation, Proc. CVPR 2010.
 |
| Results for Bending Sequence (view from above) |
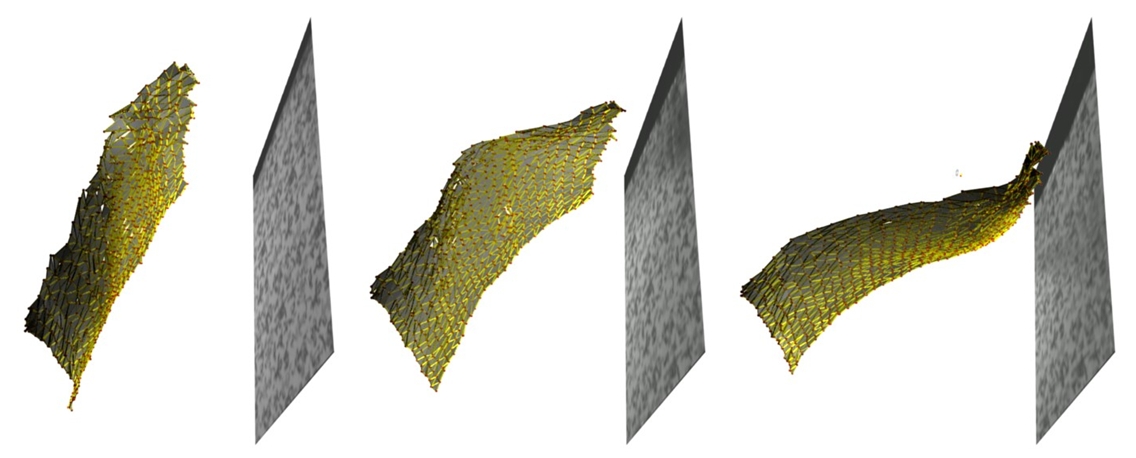 |
| Results for Silk Cloth Sequence (view from above) |
Other results, along with quantitative error analyses and comparisons, are discussed in the publication and on the project page, linked below.

Jump to Non-Rigid Motion: Introduction | Results | Publication, or Research Overview.
Publication.
Jonathan Taylor, Allan D. Jepson and Kiriakos N. Kutulakos, Non-Rigid Structure from Locally-Rigid Motion, Proc. Computer Vision and Pattern Recognition Conf., San Francisco, CA, 2010. PDF (5070KB)For more information, datasets, results and videos see our Non-Rigid Structure from Locally-Rigid Motion research project page.

Jump to Non-Rigid Motion: Introduction | Results | Publication, or Research Overview.