


Next: What to submit
Up: Description
Previous: Evaluating a polynomial
Dividing by a monic polynomial
Division of polynomials 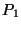 by
by 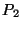 should behave like division of
integers, that is you would like to find quotient polynomial
should behave like division of
integers, that is you would like to find quotient polynomial 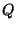 and
remainder polynomial
and
remainder polynomial 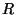 such that:
such that:
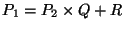
AND
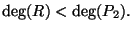
This is NOT always possible when 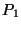 ,
, 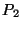 ,
, 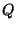 , and
, and 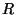 must be polynomials over the integers. For example, what quotient and
remainder would you suggest for
must be polynomials over the integers. For example, what quotient and
remainder would you suggest for 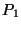
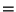
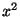 , and
, and 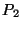
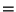
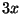 ?
?
In the special case where 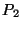 has leading (highest) coefficient
either 1 or -1 (that is,
has leading (highest) coefficient
either 1 or -1 (that is, 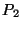 is monic), and
is monic), and 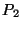 has degree no
greater than
has degree no
greater than 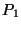 , then division is possible. Here's a recipe:
, then division is possible. Here's a recipe:
- Set the remainder
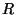 initially equal to
initially equal to 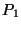 , and the quotient
, and the quotient
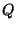 initially equal to 0.
initially equal to 0.
- While the degree of
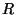 is no less than the degree of
is no less than the degree of 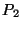 do
the following steps:
do
the following steps:
- Construct a monomial
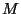 (a polynomial with one term)
(a polynomial with one term) 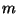 by raising
by raising
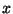 (or whatever variable you're using) to the exponent equal to the
degree of
(or whatever variable you're using) to the exponent equal to the
degree of 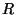 minus the degree of
minus the degree of 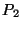 , and then multiplying this
power of
, and then multiplying this
power of 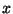 by the leading coefficient of
by the leading coefficient of 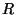 times the leading
coefficient of
times the leading
coefficient of 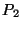 (either 1 or -1).
(either 1 or -1).
- Recalculate
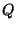 by adding
by adding 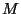 to it.
to it.
- Recalculate
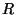 by subtracting (
by subtracting (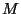
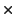
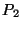 ) from it. This
new remainder will have lower degree than the old one.
) from it. This
new remainder will have lower degree than the old one.
Implement the function monDiv specified in
Polynomial.h. For 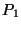 or order
or order 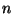 , your function should have complexity
, your function should have complexity 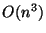 .
.



Next: What to submit
Up: Description
Previous: Evaluating a polynomial
Danny Heap
2002-09-20
![]() by
by ![]() should behave like division of
integers, that is you would like to find quotient polynomial
should behave like division of
integers, that is you would like to find quotient polynomial ![]() and
remainder polynomial
and
remainder polynomial ![]() such that:
such that:
![]() has leading (highest) coefficient
either 1 or -1 (that is,
has leading (highest) coefficient
either 1 or -1 (that is, ![]() is monic), and
is monic), and ![]() has degree no
greater than
has degree no
greater than ![]() , then division is possible. Here's a recipe:
, then division is possible. Here's a recipe:
![]() or order
or order ![]() , your function should have complexity
, your function should have complexity ![]() .
.