Evaluating a polynomial

Suppose you want to know the value of $a_n x^n$ $+$ $\cdots$ $+$ $a_1 x$ $+$ $a_0$ when $x$ has a particular value. Here is an example of a really inefficient way to evaluate the polynomial, once you've set $x$ to a particular value (e.g. $x= 7$):

$$a_n * \underbrace{x * \cdots * x}_{n  \text{times}} + a_{n-1} * \underbrace{x * \cdots * x}_{(n-1)  \text{times}} + \cdots + a_1 * x + a_0.$$

The problem is that this method uses $n-1$ $+$ $n-2$ $+$ $\cdots$ $+$ $1$ (for a total of $[(n-1)n]/2$) multiplications, and $n$ additions. You can rewrite the polynomial, using Cramer's rule, as:

$$a_0 + x*(a_1 + x*(a_2 + \cdots + x*(a_n) \cdots ))$$

This reduces the number of multiplications to $n$, and preserves the number of additions.

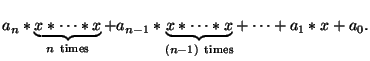
The zero polynomial evaluates to 0 for every $x$.

Implement the function eval specified in Polynomial.h. Be sure to check whether your result, or any of your intermediate results, falls outside $\pm$INT_MAX (in which case you should return INT_MAX). For a polynomial of order $n$, your function should have complexity $O(n)$.