This section reviews the basic material from Carpenter (1992), Chapters 1--10, which is necessary to use ALE.
ALE is a language with strong typing. What this means is that every structure it uses comes with a type. These types are arranged in an inheritance hierarchy, whereby type constraints on more general types are inherited by their more specific subtypes, leading to what is known as inheritance-based polymorphism. Inheritance-based polymorphism is a cornerstone of object-oriented programming. In this section, we discuss the organization of types into an inheritance hierarchy. Thus many types will have subtypes, which are more specific instances of the type. For instance, person might have subtypes male and female.
ALE does much of its processing of types at compile time, as it is reading and processing the grammar file. Thus the user is required to declare all of the types that will be used along with the subtyping relationship between them. An example of a simple ALE type declaration is as follows:
bot sub [b,c]. % two basic types -- b and c
b sub [d,e].
d sub [g,h].
e sub [].
c sub [d,f]. % b and c unify to d
f sub [].
There are quite a few things to note about this declaration. The
types declared here are bot, b, c, d, e, f and
g. Note that each type that is mentioned gets its own specification.
Of course, the whitespace is not important, but it is convenient to
have each type start its own line. A simple type specification
consists of the name of the type, followed by the keyword
sub , followed by a list of its subtypes (separated by
whitespace). In this case, bot has two subtypes, b and
c, while f, d and e have no subtypes. The subtypes
are specified by a Prolog list. In this case, a Prolog list consists
of a sequence of elements separated by commas and enclosed in square
brackets. Note that no whitespace is needed between the list brackets
and types, between the types and commas, or between the final bracket
and the period. Whitespace is only needed between constants. The
extra whitespace on successive lines is conventional, indicating the
level in the ordering for the user, but is ignored by the program.
Also notice that there are comments on two of the lines; recall that
comments begin with a
% sign and continue the length of the line.
The relation of subtyping is only specified one step at a time, but is taken to be transitive. Thus, in the example, d is a subtype of c, and c is a subtype of bot, so d is also a subtype of bot. The user only needs to specify the direct subtyping relationship. The transitive closure of this relation is computed by the compiler. While redundant specifications, such as putting d directly on the subtype list of bot, will not alter the behavior of the compiler, they are confusing to the reader of the program and should be avoided. In addition, the derived transitive subtyping relationship must be anti-symmetric. In particular, this means that there should not be two distinct types each of which is a subtype of the other.
There are two additional restrictions on the inheritance hierarchy beyond the requirement that it form a partial order. First, there is a special type bot, which must be declared as the unique most general type. In other words, every type must be a subtype of bot. Removing the declaration of bot would violate this condition, as would adding an additional specification, such as simply adding j sub [k,l], as j would not be a subtype of bot, or a declaration m sub [bot], as bot would no longer be the most general type.
The second and more subtle restriction on type hierarchies is that they be bounded complete. Since type declarations must be finite, this amounts to the restriction that every pair of types which have a common subtype have a unique most general common subtype. In the case at hand, b and c have three common subtypes, d, g, and h. But these subtypes of b and c are ordered in such a way that d is the most general type in the set, as both g and h are subtypes of d. An example of a type declaration violating this condition is:
bot sub [a,b].
a sub [c,d].
c sub [].
d sub [].
b sub [c,d].
The problem here is that while a and b have two common
subtypes, namely c and d, they do not have a most general
common subtype, since c is not a subtype of d, and d
is not a subtype of c. In general, a violation of the bounded
completeness condition such as is found in this example can be patched
without destroying the ordering by simply adding additional types.
In this case, the following type hierarchy preserves all of the
subtyping relations of the one above, but satisfies bounded
completeness:
bot sub [a,b].
a sub [e].
e sub [c,d].
c sub [].
d sub [].
b sub [e].
In this case, the new type e is the most general subtype of
a and b.
This last example brings up another point about inheritance hierarchies. When a type only has one subtype, the system provides a warning message (as opposed to an error message). This condition will not cause any compile-time or run-time errors, and is perfectly compatible with the logic of the system. It is simply not a very good idea from either a conceptual or implementational point of view. For more on this topic, see Carpenter (1992:Chapter 9).
The primary representational device in ALE is the typed feature structure. In phrase structure grammars, feature structures model categories, while in the definite clause programs, they serve the same role as first-order terms in Prolog, that of a universal data structure. Feature structures are much like the frames of AI systems, the records of imperative programming languages like C or Pascal, and the feature descriptions used in standard linguistic theories of phonology, and more recently, of syntax.
Rather than presenting a formal definition of feature structures, which can be found in Carpenter (1992:Chapter 2), we present an informal description here. In fact, we begin by discussing feature structures which are not necessarily well-typed. In the next section, the type system is presented.
A feature structure consists of two pieces of information. The first is a type. Every feature structure must have a type drawn from the inheritance hierarchy. The other kind of information specified by a feature structure is a finite, possibly empty, collection of feature/value pairs. A feature value pair consists of a feature and a value, where the value is itself a feature structure. The difference between feature structures and the representations used in phonology and in GPSG, for instance, is that it is possible for two different substructures (values of features at some level of nesting) to be token identical in a feature structure. Consider the following feature structure drawn from the lexical entry for John in the categorial grammar in the appendix, displayed in the output notation of ALE:
cat
QSTORE e_list
SYNSEM basic
SEM j
SYN np
The type of this feature structure is cat, which is interpreted
to mean it is a category. It is defined for two features,
QSTORE and SYNSEM. As can be seen from this example, we follow
the HPSG notational convention of displaying features in all caps,
while types are displayed in lower case. Also note that features and
their values are printed in alphabetic order of the feature names.
In this case, the value of the QSTORE feature is
the simple feature structure of type e_list,
which has no feature
values. On the other hand, the feature SYNSEM has a complex
feature as its value, which is of type basic, and has two feature
values SEM and SYN, both of which have simple values.
This last feature structure doesn't involve any structure sharing. But consider the lexical entry for runs:
cat
QSTORE e_list
SYNSEM backward
ARG basic
SEM [0] individual
SYN np
RES basic
SEM run
RUNNER [0]
SYN s
Here there is structure sharing between the path SYNSEM ARG SEM
and the path SYNSEM RES SEM RUNNER, where a path is simply
a sequence of features. This structure sharing is indicated by the
tag [0]. In this case, the sharing indicates that the
semantics of the argument of runs fills the runner role in the
semantics of the result. Also note that a shared structure is only
displayed once; later occurrences simply list the tag. Of course,
this example only involves structure sharing of a very simple feature
structure, in this case one consisting of only a type with no
features. In general, structures of arbitrary complexity may be
shared, as we will see in the next example.
ALE, like Prolog II and HPSG, but unlike most other systems, allows cyclic structures to be processed and even printed. For instance, consider the following representation we might use for the liar sentence This sentence is false:
[0] false
ARG1 [0]
In this case, the empty path and the feature ARG1 share a value.
Similarly, the path ARG1 ARG1 ARG1 and the path ARG1 ARG1,
both of which are defined, are also identical. But consider a
representation for the negation of the liar sentence, It is false
that this sentence is false:
false
ARG1 [0] false
ARG1 [0]
Unlike Prolog II, ALE does not necessarily treat these two feature
structures as being identical, as it does not conflate a cyclic
structure with its infinite unfolding. We take up the notion of
token identical structures in the section below on extensionality.
It is interesting to note that with typed feature structures, there is a choice between representing information using a type and representing the same information using feature values. This is a familiar situation found in most inheritance-based representation schemes. Thus the relation specified in the value of the path SYNSEM RES SEM is represented using a type, in:
SEM run
RUNNER [0]
An alternative encoding, which is not without merit, is:
SEM unary_rel
REL run
ARG1 [0]
In general, type information is processed much more efficiently than
feature value information, so as much information as possible should
be placed in the types. The drawback is that type information must be
computed at compile-time and remain accessible at run-time. More
types simply require more memory.
Feature structures are inherently partial in the information they provide. Based on the type inheritance ordering, we can order feature structures based on how much information they provide. This ordering is referred to as the subsumption ordering. The notion of subsumption, or information containment, can be used to define the notion of unification, or information combination. Unification conjoins the information in two feature structures into a single result if they are consistent and detects an inconsistency otherwise.
We define subsumption, saying that F subsumes G, if and only if:
agr < agr
PERS first PERS first
NUM plu
sign phrase
SUBJ agr < SUBJ agr
PERS pers PERS first
NUM plu
sign sign
SUBJ agr SUBJ [0] agr
PERS first PERS first
NUM plu < NUM plu
OBJ agr OBJ [0]
PERS first
NUM plu
false false [1] false
ARG1 false < ARG1 [0] false < ARG1 [1]
ARG1 false ARG1 [0]
Note that the second of these subsumptions holds only if pers is
a more general type than first, and sign is a more general
type than phrase. It is also important to note that the feature
structure consisting simply of the type bot will subsume every
other structure, as the type bot is assumed to be more general
than every other type.
Unification is an operation defined over pairs of feature structures that combines the information contained in both of them if they are consistent and fails otherwise. In ALE, unification is very efficient.
Declaratively, unifying two feature structures computes a result which
is the most general feature structure subsumed by both input
structures. But the operational definition is more enlightening, and
can be given by simple conditions which tell us how to unify two
structures. We begin by unifying the types of the structures in the
type hierarchy. This is why we required the bounded completeness
condition on our inheritance hierarchies; we want unification to
produce a unique result. If the types are inconsistent, unification
fails. If the types are consistent, the resulting type is the
unification of the input types. Next, we recursively unify all of the
feature values of the structures being unified which occur in both
structures. If a feature only occurs in one structure, we copy it
over into the result. This algorithm terminates because we only need
to unify structures which are non-distinct and there are a finite
number of nodes in any input structure.
Some examples of unification follow, where we use + to represent the operation:
agr + agr = agr
PERS first NUM plu PERS first
NUM sing
sign sign sign
SUBJ agr + SUBJ [0] bot = SUBJ [0] agr
PERS 1st OBJ [0] PERS first
OBJ agr NUM plu
NUM plu OBJ [0]
t t t
F [0] t + F t = F [1] t
G [0] F [1] F [1]
G [1] G [1]
agr + agr = *failure* PERS first PERS second
e_list + ne_list = *failure*
HD a
TL e_list
Note that the second example respects our assumption that the type
bot is the most general type, and thus more general than
agr. The second example illustrates what happens in a simple case of
structure sharing: information is retrieved from both the SUBJ
and OBJ and shared in the result. The third example shows how
two structures without cycles can be unified to produce a structure
with a cycle. Just as the feature structure bot subsumes every
other structure, it is also the identity with respect to unification;
unifying the feature structure consisting just of the type bot
with any feature structure F results simply in F. The last two
unification attempts fail, assuming that the types first and
second and the types e_list and ne_list are
incompatible.
As we mentioned in the introduction, what distinguishes ALE from other approaches to feature structures and most other approaches to terms, is that there is a strong type discipline enforced on feature structures. We have already demonstrated how to define a type hierarchy, but that is only half the story with respect to typing. The other component of our type system is a notion of feature appropriateness, whereby each type must specify which features it can be defined for, and furthermore, which types of values such features can take. The notion of appropriateness used here is similar to that found in object-oriented approaches to typing. For instance, if a feature is appropriate for a type, it will also be appropriate for all of the subtypes of that type. In other words, appropriateness specifications are inherited by a type from its supertypes. Furthermore, value restrictions on feature values are also inherited. Another important consideration for ALE's type system is the notion of type inference, whereby types for structures which are underspecified can be automatically inferred. This is a property our system shares with the functional language ML, though our notion of typing is only first-order. To further put ALE's type system in perspective, we note that type inheritance must be declared by the user at compile time, rather than being inferred. Furthermore, types in ALE are semantic, in Smolka's (1988b) terms, meaning that types are used at run-time. Even though ALE employs semantic typing, the type system is employed statically (at compile-time) to detect type errors in grammars and programs.
As an example of an appropriateness declaration, consider the simple type specification for lists with a head/tail encoding:
bot sub [list,atom].
list sub [e_list,ne_list].
e_list sub [].
ne_list sub []
intro [hd:bot,
tl:list].
atom sub [a,b].
a sub [].
b sub [].
This specification tells us that a list can be either empty (
e_list) or non-empty ( ne_list). It implicitly tells us that a
non-empty list can not have any features defined for it, since none
are declared directly or inherited from more general types. The
declaration also tells us that a non-empty list has two features,
representing the head and the tail of a list, and, furthermore, that
the head of a list can be anything (since every structure is of type
bot), but the tail of the list must itself be a list. Note that
features must also be Prolog constants, even though the output
routines convert them to all caps.
In ALE, every feature structure must respect the appropriateness restrictions in the type declarations. This amounts to two restrictions. First, if a feature is defined for a feature structure of a given type, then that type must be appropriate for the feature. Furthermore, the value of the feature must be of the appropriate type, as declared in the appropriateness conditions. The second condition goes the other way around: if a feature is appropriate for a type, then every feature structure of that type must have a value for the feature. A feature structure respecting these two conditions is said to be totally well-typed in the terminology of Carpenter (1992, Chapter 6).
For instance, consider the following feature structures:
list HD a TL bot
ne_list
HD bot
TL ne_list
HD atom
TL list
ne_list
HD [0] ne_list
HD [0]
TL [0]
TL e_list
The first structure violates the typing condition because the type
list is not appropriate for any features, only ne_list is.
But even if we were to change its type to ne_list, it would
still violate the type conditions, because bot is not an
appropriate type for the value of TL in a ne_list. On
the other hand, the second and third structures above are totally
well-typed. Note that the second such structure does not specify what
kind of list occurs at the path TL TL, nor does it specify what
the HD value is, but it does specify that the second element of
the list, the TL HD value is an atom, but it doesn't
specify which one.
To demonstrate how inheritance works in a simple case, consider the specification fragment from the categorial grammar in the appendix:
functional sub [forward,backward]
intro [arg:synsem,
res:synsem].
forward sub [].
backward sub [].
This tells us that functional objects have ARG and
RES features. Because forward and backward are subtypes
of functional, they will also have ARG and RES
features, with the same restrictions.
There are a couple of important restrictions placed on appropriateness conditions in ALE. The most significant of these is the acyclicity requirement. This condition disallows type specifications which require a type to have a value which is of the same or more specific type. For example, the following specification is not allowed:
person sub [male,female]
intro [father:male,
mother:female].
male sub [].
female sub [].
The problem here is the obvious one that there are no most general
feature structures that are both of type person and totally
well-typed.
This is because any person must have a father and mother feature,
which are male and female respectively, but since male and female are
subtypes of person, they must also have mother and father values. It
is significant to note that the acyclicity condition does not rule out
recursive structures, as can be seen with the example of lists. The
list type specification is acceptable because not every list is
required to have a head and tail, only non-empty lists are. The
acyclicity restriction can be stated graph theoretically by
constructing a directed graph from the type specification. The nodes
of the graph are simply the types. There is an edge from every type
to all of its supertypes, and an edge from every type to the types in
the type restrictions in its features. Type specifications are only
acceptable if they produce a graph with no cycles. One cycle in the
person graph is from male to person (by the
supertype relation) and from person to male (by the
FATHER feature). On the other hand, there are no cycles in the
specification of list.
The second restriction placed on appropriateness declarations is designed to limit non-determinism in much the same way as the bounded completeness condition on the inheritance hierarchy. This second condition requires every feature to be introduced at a unique most general type. In other words, the set of types appropriate for a feature must have a most general element. Thus the following type declaration fragment is invalid:
a sub [b,c,d].
b sub []
intro [f:w,
g:x].
c sub []
intro [f:y,
h:z].
d sub [].
The problem is that the feature F is appropriate for types
b and c, but there is not a unique most general type for which
it's appropriate. In general, just like the bounded completeness
condition, type specifications which violate the feature introduction
condition can be patched, without violating any of their existing
structure, by adding additional types. In this case, we add a new type
between a and the types b and c, producing the
equivalent well-formed specification:
a sub [e,d].
e sub [b,c]
intro [f:bot].
b sub []
intro [f:w,
g:x].
c sub []
intro [f:y,
h:z].
d sub [].
This example also illustrates how subtypes of a type can place
additional restrictions on values on features as well as introducing
additional features.
As a further illustration of how feature introduction can be obeyed in general, consider the following specification of a type system for representing first-order terms:
sem_obj sub [individual,proposition].
individual sub [a,b].
a sub [].
b sub [].
proposition sub [atomic_prop,relational].
atomic_prop sub [].
relational_prop sub [unary_prop,transitive_prop]
intro [arg1:individual].
unary_prop sub [].
transitive_prop sub [binary_prop,ternary_prop]
intro [arg2:individual].
binary_prop sub [].
ternary_prop sub []
intro [arg3:individual].
In this case, unary propositions have one argument feature, binary
propositions have two argument features, and ternary propositions have
three argument features, all of which must be filled by individuals.
ALE also respects the distinction between intensional and
extensional types (see Carpenter (1992:Chapter 8). The concept
of extensional typing has its origins in the assumption in standard
treatments of feature structures, that there can only be one copy of
any atom (a feature structure with no appropriate features) in a
feature structure. Thus, if path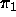 
leads to atom a, and
path 
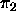leads to atom a, then the values for those two
paths are token-identical. Token-identity refers to an identity
between two feature structures with respect to the objects themselves,
as opposed to structure-identity, which refers to an identity
between two feature structures with respect to the information they
contain, i.e. whether their combined information could be construed as
information about the same object.
Smolka (1988a) partitioned his atoms according to whether more than one copy could exist or not. In ALE, following Carpenter (1992), this notion of copyability has been extended to arbitrary types -- loosely speaking, those types which are copyable we call intensional, and those which are not we call extensional. Thus, it is possible to have two feature structures of the same intensional type which, although they may be structure-identical, are not token-identical. Formally:
Given the set of types, Type, defined by an ALE signature, we designate a subset,The restriction of ExtType to maximally specific sorts is peculiar to ALE, and is levied in order to reduce the computational complexity of enforcing extensionality., as the set of extensional types. This set consists only of maximally specific types, i.e. for each
, there is no type
such that
subsumes
.
We need one more definition to formally state the effect which an extensional type has on feature structures in ALE.
Given a set of extensional types, ExtType, we define an equivalence relation,In ALE, all feature structures behave as if they are what Carpenter (1992) referred to as collapsed. That is, the only collapsing relation which exists between any two feature structures is the trivial collapsing relation, namely:, the collasping relation, on well-typed feature structures, such that
for
only if:
has the same type,
, as
, and
, and
- for every feature, f, appropriate to
,
, the value of f in
, and
, the value of f in
, are defined, and
.
In the case of acyclic feature structures, this definition is equivalent to saying that two feature structures of the same extensional type are token-identical if and only if, for every feature appropriate to that type, their respective values on that feature are token-identical. For example, supposing that we have a signature representing dates, then the two substructures representing dates in the following structure must be token identical.if and only if
is token-identical to
.
married_person
BIRTHDAY [1] date
DAY 12
MONTH nov
YEAR 1971
SPOUSE BIRTHDAY [2] date
DAY 12
MONTH nov
YEAR 1971
In other words, this represents a person born on 12 November 1971, who
is married to a person with the same birthdate.
Now consider a slightly more complex example, which employs the following signature.
bot sub [a,b,c,g].
a sub []
intro [f:b,g:c].
b sub [].
c sub [].
g sub []
intro [h:a,j:a].
If a, b, and c are extensional, then the values of
H and J in g are always token-identical:
g
H [0] a
F b
G c
J [0]
But if only a, and b are extensional, and c is
intensional, then the values of H and J are not
necessarily token-identical, although, they are always
structure-identical:
g
H a
F [1] b
G c
J a
F [1]
G c
To cite an earlier example, suppose we were to specify that the type false, used in the liar sentence and its negation, were extensional. Thus, we would specify:
ext([Now the liar sentence's representation is:, false,
]).
[0] false
ARG1 [0]
as before, but the negation of the liar sentence would also be
represented by:
[0] false
ARG1 [0]
since if were still represented by:
[1] false
ARG1 [0] false
ARG1 [0]
then we could cite a non-trivial collasping relation,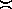 
, in
which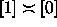 
.
A related example involves the following standard example.
s
A [0] t
C [0]
B [1] t
C [1]
Assuming that t is extensional and only appropriate for the
feature C, then the structures [0] and [1] in the
above structure would be identified.
Extensionality allows the proper representation of feature structures and terms in both PATR-II, the Rounds-Kasper system, and in Prolog and Prolog II. For PATR-II and the Rounds-Kasper system, all atoms (those types with no appropriate features) are assumed to be extensional. Furthermore, in the Rounds-Kasper and PATR-II systems, which are monotyped, there is only one type that is appropriate for any features, and it must be appropriate for all features in the grammar. In Prolog and Prolog II, the type hierarchy is assumed to be flat, and every type is extensional.
Just as with implementations of Prolog, collapsing is only performed as it is needed. As shown by Carpenter (1992), collapsing can be restricted to cases where inequations are tested between two structures, with exactly the same failure behavior. It turned out to be less efficient to collapse structures before asserting them into the chart, primarily because the time to compare arbitrary structures for collapsibility is cubic in the size of the structure being collapsed. See the section below on inequations for further discussion. The most obvious ramification of this decision is that the I/O routines will not automatically collapse structures before printing them.
Extensional types in ALE are specified all at once in a list:
in the same file in which the subsumption relation is defined. All types which are not mentioned in the ext specification are assumed to be intensional. If more than one ext specification is given, the first one is used. If no ext specification is given, then the specification: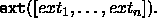
ext([]).is assumed.
Of course, collapsing is only enforced between feature structures whose life-spans in ALE
overlap. So, for example, if one request
is given for the representation of the liar sentence:
[0] false
ARG1 [0]
and then another is given for that of its negation, the output is not:
[0](referring to the same token above) but rather:
[0] false
ARG1 [0]
Every time a new context arises, numbering of structures begins again
from [0].
Currently, extensionality is only enforced before the answer to a top-level query is given.
Feature structures may also incorporate inequality constraints, following (Carpenter 1992), which is in turn based on the notion of inequation in Prolog II (Colmerauer 1987). For instance, we might have the following representation of the semantics of a sentence:
SEM binary_rel
REL know
ARG1 [0] referent
GENDER masc
PERS third
NUM sing
ARG2 [1] referent
GENDER masc
PERS third
NUM sing
[0] =\= [1]
Below the feature information, we have included the constraint that
the value of the structure [0] is not identical to that of structure
[1]. As a result, we cannot unify this structure with the
following one.
REL know ARG1 [2] ARG2 [2]Any attempt to unify the structures [0] and [1] causes failure.
Furthermore, any attempt to inequate two extensionally identical structures will cause failure. For instance, consider the following.
s s
F [1] t F [3]
H [1] + G [4] = failure
G [2] t [3] =\= [4]
H [1]
The values of the features F and G cannot be inequated
because they are extensionally identical (assuming the type t is
declared to be extensional and is only appropriate for the feature
H.
When inequations are evaluated, they are reduced. For instance, consider the following:
F [1] s
H bot
J bot
G [2] s
H bot
J bot
[1] =\= [2]
If the type s is extensional and appropriate for the features
H and J, then the inequation above is reduced to the
following.
F [1] s
H [3] bot
J [4] bot
G [2] s
H [5]
J [6]
[3] =\= [5] ; [4] =\= [6]
The set of inequations is stored in conjunctive normal form. The cost
is some space over the re-evaluation of inequations. Of course, if
the types on [3] and [4] were more refined than bot,
then the inequations [3] =\= [5] and [4] =\=
[6] would further reduce. In addition, when reducing inequations in
this way, we eliminate those that are trivially satisfied. The ones
that are printed are only the residue after reduction. For instance,
consider the following structure:
F [1] s
H a
J bot
G [2] s
H b
J bot
[1] =\= [2]
Assuming that a and b are not unifiable, then this
structure reduces to the following.
F s
H a
J [3] bot
G s
H b
J [4] bot
[3] =\= [4]
If structures [3] and [4] had begun with ununifiable
types, then there would be no residual inequation.
An important subcase is that of inequality between extensional atoms. If atoms are extensional, then every instance is identical. Thus an inequality between two identical, extensional atoms fails.
Now that we have seen how the type system must be specified, we turn our attention to the specification of feature structures themselves. The most convenient and expressive method of describing feature structures is the logical language developed by Kasper and Rounds (1986), which we modify here in three ways. First, we replace the notion of path sharing with the more compact and expressive notion of variable due to Smolka (1988a). Second, we extend the language to types, following Pollard (in press). Finally, we add inequations.
The collection of descriptions used in ALE can be described by the following BNF grammar:
<desc> ::= <type>
| <variable>
| (<feature>:<desc>)
| (<desc>,<desc>)
| (<desc>;<desc>)
| (=\= <desc>)
As we have said before, both types and features are represented by
Prolog constants. Variables, on the other hand, are represented by
Prolog variables. As indicated by the BNF, no whitespace is
needed around the feature selecting colon, conjunction
comma and disjunction semi-colon , but any
whitespace occurring will be ignored.
These descriptions are used for picking out feature structures that
satisfy them. We consider the clauses of the definition in turn. A
description consisting of a type picks out all feature structures of
that type. A variable can be used to refer to any feature structure,
but multiple occurrences of the same variable must refer to the same
structure. A description of the form
(<feature>:<desc>) picks out a feature structure whose
value for the feature satisfies the nested description. An inequation
=
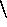= <desc> causes the embedded description to be
evaluated, and the current structure to be inequated with it. The
resulting inequations are both symmetric and persistent; as long
as the feature structures remain, they can never be unified.
There are two ways of logically combining descriptions: following Prolog, the comma represents conjunction and the semi-colon represents disjunction. A feature structure satisfies a conjunction of descriptions just in case it satisfies both conjuncts, while it satisfies a disjunction of descriptions if it satisfies either of the disjuncts.
We should also add to the above BNF grammar the following line:
<desc> ::= (<path> == <path>)This is an equational description , of which inequations are the negation. Note, however, that while inequations are satisfied by the absence of token-identity, equational descriptions are satisfied by the existence of structure-identity (i.e. the arguments are unifiable), although it creates token-identity by unifying its arguments. All instances of equational descriptions can be captured by using multiple occurrences of variables. For example, the description:
([arg1]==[arg2])is equivalent to the description:
(arg1:X,arg2:X).modulo other occurrences of X.
Standard assumptions about operator precedence and association are followed by ALE, allowing us to omit most of the parentheses in descriptions. In particular, equational descriptions bind the most tightly, followed by feature selecting colon, then by inequations, then conjunction and finally disjunction. Furthermore, conjunction and disjunction are left-associative, while the feature selector is right-associative. For instance, this gives us the following equivalences between descriptions:
a, b ; c, d ; e = (a,b);(c,d);e a,b,c = a,(b,c) f:g:bot,h:j = (f:(g:bot)),(h:j) f:g: =\=k,h:j = (f:(g: =\=(k))),(h:j) f:[g]==[h],h:j = (f:([g]==[h])),(h:j)Note that a space must occur between =
= and other
operators such as :.
A description may be satisfied by no structure, a finite number of
structures or an infinite collection of feature structures. A
description is said to be satisfiable if it is satisfied by at
least one structure. A description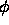 
entails a description
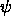if every structure satisfying 
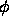also satisfies 
.
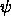Two descriptions are logically equivalent if they entail each
other, or equivalently, if they are satisfied by exactly the same set
of structures.
ALE is only sensitive to the differences between logically equivalent formulas in terms of speed. For instance, the two descriptions (tl:list,ne_list,hd:bot) and hd:bot are satisfied by exactly the same set of totally well-typed structures assuming the type declaration for lists given above, but the smaller description will be processed much more efficiently. There are also efficiency effects stemming from the order in which conjuncts (and disjuncts) are presented. The general rule for speedy processing is to eliminate descriptions from a conjunction if they are entailed by other conjuncts, and to put conjuncts with more type and feature entailments first. Thus with our specification for relations above, the description (arg1:a, binary_proposition) would be slower than (binary_proposition,arg1:a), since binary_proposition entails the existence of the feature arg1, but not conversely.
At run-time, ALE computes a representation of the most general feature structure which satisfies a description. Thus a description such as hd:a with respect to the list grammar is satisfied by the structure:
ne_list HD a TL listEvery other structure satisfying the description hd:a is subsumed by the structure given above. In fact, the above structure is said to be a vague representation of all of the structures that satisfy the description. The type conditions in ALE were devised to obey the very important property, first noted by Kasper and Rounds (1986), that every non-disjunctive description is satisfied by a unique most general feature structure. Thus in the case of hd:a, there is no more general feature structure than the one above which also satisfies hd:a.
The previous example also illustrates the kind of type inference used by ALE. Even though the description hd:a does not explicitly mention either the feature TL or the type ne_list, to find a feature structure satisfying the description, ALE must infer this information. In particular, because ne_list is the most general type for which HD is appropriate, we know that the result must be of type ne_list. Furthermore, because ne_list is appropriate for both the features HD and TL, ALE must add an appropriate TL value. The value type list is also inferred, due to the fact that a ne_list must have a TL value which is a list. As far as type inference goes, the user does not need to provide anything other than the type specification; the system computes type inference based on the appropriateness specification. In general, type inference is very efficient in terms of time. The biggest concern should be how large the structures become.
In contrast to a vague description, a disjunctive description is
usually ambiguous. Disjunction is where the complexity arises
in satisfying descriptions, as it corresponds operationally to
non-determinism.
For instance, the description hd:(a;b)
is satisfied by two distinct minimal structures, neither of which
subsumes the other:
ne_list ne_list HD a HD b TL list TL listOn the other hand, the description hd:atom is satisfied by the structure:
ne_list HD atom TL listEven though the descriptions hd:atom and hd:(a;b) are not logically equivalent (though the former entails the latter), they have the interesting property of being unifiable with exactly the same set of structures. In other words, if a feature structure can be unified with the most general satisfier of hd:atom, then it can be unified with one of the minimal satisfiers of hd:(a;b).
In terms of efficiency, it is very important to use vagueness wherever possible rather than ambiguity. In fact, it is almost always a good idea to arrange the type specification with just this goal in mind. For instance, consider the difference between the following pair of type specifications, which might be used for English gender:
gender sub [masc,fem,neut]. gender sub [animate,neut].
masc sub []. animate sub [masc,fem].
fem sub []. masc sub [].
neut sub []. fem sub [].
neut sub [].
Now consider the fact that the relative pronouns who and
which are distinguished on the basis of whether they select animate
or inanimate genders. In the flatter hierarchy, the only way to
select the animate genders is by the ambiguous description
masc;fem. The hierarchy with an explicit animate type can capture
the same possibilities with the vague description animate. An
effective rule of thumb is that ALE does an amount of work at
best proportional to the number of most general satisfiers of a
description and at worst proportional to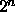 
, where n is the
number of disjuncts in the description. Thus the ambiguous
description requires roughly twice the time and memory to process than
the vague description. Whether the amount of work is closer to the
number of satisfiers or exponential in the number of disjuncts depends
on how many unsatisfiable disjunctive possibilities drop out early in
the computation.
Inequations are persistent in that once that are created, they remain as long as one of the structures being inequated remains. Thus the following two descriptions are logically equivalent.
f:(=\=c), f:c f:c, f:(=\=c)Both will cause failure. But they are not operationally equivalent. An inequation is evaluated when it arises, and again after high-level unifications in the system. But as we mentioned before, inequations are not evaluated every time an inequated structure is modified. Also, the complexity is sensitive to the conjunctive normal form of the inequation at the time at which it is evaluated, though it may later be reduced.
Although inequations are persistent, they are not constantly enforced by ALE. In an ideal system, inequations would be attached directly to structures so that they could be evaluated on-line during unification. As things stand, ALE 2.0 represents a structure by combining a regular feature structure and a set of inequations.
These sets of inequations are evaluated at run-time at the point they are encountered, before answers are given to top-level queries, before any edge is added to ALE's parsing chart, after every daughter is matched to a description in an ALE grammar rule
,
and after the head of an ALE definite clause has been matched
to a goal. At compile-time, inequations are checked for every empty
category, for every lexical entry, and after every lexical rule
application.
ALE allows the user to employ a general form of parametric macros in descriptions. Macros allow the user to define a description once and then use a shorthand for it in other descriptions. We first consider a simple example of a macro definition, drawn from the categorial grammar in the appendix. Suppose the user wants to employ a description qstore:e_list frequently within a program. The following macro definition can be used in the program file:
quantifier_free macro
qstore:e_list.
Then, rather than including the description qstore:e_list in
another description, @ quantifier_free can be used instead.
Whenever @ quantifier_free is used, qstore:e_list is
substituted.
In the above case, the <macro_spec> was a simple atom, but in general, it can be supplied with arguments. The full BNF for macro definitions is as follows:
<macro_def> ::= <macro_head> macro <desc>.
<macro_head> ::= <macro_name>
| <macro_name>(<seq(<var>)>)
<macro_spec> ::= <macro_name>
| <macro_name>(<seq(<desc>)>)
<seq(X)> ::= X
| X, <seq(X)>
Note that <seq(X)> is a parametric category in the BNF
which abbreviates non-empty sequences of objects of category X.
The following clause should be added to recursive definition of
descriptions:
<desc> ::= @ <macro\_spec>A feature structure satisfies a description of the form @ <macrospec> just in case the structure satisfies the body of the definition of the macro.
Again considering the categorial grammar in the appendix, we have the following macros with one and two arguments respectively:
np(Ind) macro
syn:np,
sem:Ind.
n(Restr,Ind) macro
syn:n,
sem:(body:Restr,
ind:Ind).
In general, the arguments in the definition of a macro must be Prolog
variables, which can then be used as variables in the body of the
macro. With the first macro, the description @ np(j) would then
be equivalent to the description syn:np,sem:j. When evaluating
a macro, the argument supplied, in this case j, is substituted
for the variable when expanding the macro. In general, the argument
to a macro can itself be an arbitrary description (possibly containing
macros). For instance, the description:
n((and,conj1:R1,conj2:R2),Ind3)would be equivalent to the description:
syn:n,
sem:(body:(and,conj1:R1,conj2:R2),
ind:Ind3)
This example illustrates how other variables and even complex
descriptions can be substituted for the arguments of macros.
Also note the parentheses around the arguments to the first argument
of the macro. Without the parentheses, as in
n(and,conj1:R1,conj2:R2,Ind3), the macro expansion routine would take
this to be a four argument macro, rather than a two argument macro
with a complex first argument. This brings up a related point, which
is that different macros can have the same name as long as they have
the different numbers of arguments.
Macros can also contain other macros, as illustrated by the macro for proper names in the categorial grammar:
pn(Name) macro
synsem: @ np(Name),
@ quantifier_free.
In this case, the macros are expanded recursively, so that the
description pn(j) would be equivalent to the description
synsem:(syn:np,sem:j),qstore:e_list
It is usually a good idea to use macros whenever the same description is going to be re-used frequently. Not only does this make the grammars and programs more readable, it reduces the number of simple typing errors that lead to inconsistencies.
As is to be expected, macros can't be recursive. That is, a macro, when expanded, is not allowed to invoke itself, as in the ill-formed example:
infinite_list(Elt) macro
hd:Elt,
tl:infinite_list(Elt)
The reason is simple; it is not possible to expand this macro to a
finite description. Thus all recursion must occur in grammars or
programs; it can't occur in either the appropriateness conditions or
in macros.
The user should note that variables in the scope of a macro are not the same as ALE feature structure variables --- they denote where macro-substitutions of parameters are made, not instances of re-entrancy in a feature structure. If we employ the following macro:
blah(X) macro
b,
f: X,
g: X.
with the argument (c,h:a) for example we obtain the following
feature structure:
b
F c
H a
G c
H a
where the values of F and G are not shared (unless c
and a are extensional). We can, of course, create a shared
structure using blah, by including an ALE variable in the
actual argument to the macro. Thus blah((Y,c,h:a)) yields:
b
F [0] c
H a
G [0]
Because programming with lists is so common, ALE has a special macro for it, based on the Prolog list notation. A description may also take any of the forms on the left, which will be treated equivalently to the descriptions on the right in the following diagram:
[] e_list
[H|T] (hd:H,
tl:T)
[A1,A2,...,AN] (hd:A1,
tl:(hd:A2,
tl: ...
tl:(hd:AN,
tl:e_list)...))
[A1,...,AN|T] (hd:A1,
tl:(hd:A2,
tl: ...
tl:(hd:AN,
tl:T)...))
Note that this built-in macro does not require the macro operator
@. Thus, for example, the description [a|T3] is equivalent to
hd:a,tl:T3, and the description [a,b,c] is equivalent to
hd:a,tl:(hd:b,tl:(hd:c,tl:e_list)). There are many example of
this use of Prolog's list notation in the grammars in the appendix.
Our logical language of descriptions can be used with the type system in order to enforce constraints on feature structures of a particular type. Constraints are attached to types, and may consist of arbitrary descriptions. Their effect is to require every structure of the constrained type to always satisfy the constraint description.
Constraints are enforced using the cons operator, e.g.:
bot sub [a,b].
a sub []
intro [f:b,g:b].
b sub [].
a cons (f:X,g:=\= X).
The constraint on the type a (which must occur within
parentheses) requires all feature structures of type a to have
non-token-identical values for features f and g. Notice
that the type b has no constraints expressed. This is
equivalent to the (anonymous variable) constraint specification:
b cons _.which is satisfied by any feature structure (of type b). A type constraint may use any of the operators in the description language, including further type descriptions, which may themselves be constrained.
It is crucial that the type descriptions be finitely resolvable. Because simple depth-first search is used to evaluate constraints, infinite resolution paths will cause the system to hang. For example, the following constraints would not be permitted in the following signature:
bot sub [a,b].
a sub [c]
intro [f:bot].
c sub [].
b sub []
intro [g:bot].
a cons f:b.
b cons g:c.
This is because a subsumes c. If such a cycle exists, the
user is given an error message. Notice, however, that type
constraints can be used to provide additional information regarding
value restrictions on appropriate features. An error is also given if
the constraint information is inconsistent with information given in
the appropriateness conditions. In general, ALE performs more
efficiently when restrictions are provided in the appropriateness
conditions, rather than in general constraints; but type constraints
can encode a greater variety of restrictions. Specifically, they
allow constraints to express equality and inequality, as well as
deeper path restrictions. Constraints may include relational
constraints, which are defined using definite clauses (which we
discuss below). Type constraints are are compiled in the same way as
other descriptions, which is not inefficient. Also, like
appropriateness conditions, they are only enforced once for each
structure.
It is also important to note that because of the delay in ALE's inequation enforcement, type constraints that involve recursion that terminates by an inequation failure may go into infinite loops due to this delay in enforcement. Because extensionality is only enforced before the answer to a top-level query is given, recursive type constraints that rely on the extensional identity of two feature structures to terminate on the basis of their type will not terminate.
We now provide a simplified form of the Zebra Puzzle (Figure 4.1), a common puzzle for constraint resolution. This puzzle was solved by Aït-Kaci (1984) using roughly the same methods as we use here. The puzzle illustrates the expressive power of the combination of extensional types, inequations and type constraints. Such puzzles, sometimes known as logic puzles or constraint puzzles, require one to find a state of affairs within some situation that simultaneously satisfies a set of constraints. The situation itself very often implicitly levies certain constraints.
We can represent the simplified Zebra Puzzle in ALE as:
% Subsumption
%=======================
bot sub [house,descriptor,background].
descriptor sub [nat_type,ani_type,bev_type].
nat_type sub [norwegian,ukranian,spaniard].
norwegian sub [].
ukranian sub [].
spaniard sub [].
ani_type sub [fox,dog,zebra].
fox sub [].
dog sub [].
zebra sub [].
bev_type sub [juice,tea,milk].
juice sub [].
tea sub [].
milk sub [].
house sub []
intro [nationality:nat_type,animal:ani_type,beverage:bev_type].
background sub [clue]
intro [house1:house,house2:house,house3:house].
clue sub [maximality].
maximality sub [].
ext([norwegian,ukranian,spaniard,fox,dog,zebra,juice,tea,milk]).
% Constraints
%=============================
background cons
(house1:nationality:N1, % inequational constraints
house2:nationality:(N2,(=\= N1)),
house3:nationality:((=\= N1),(=\= N2)),
house1:animal:A1,
house2:animal:(A2,(=\= A1)),
house3:animal:((=\= A1),(=\= A2)),
house1:beverage:B1,
house2:beverage:(B2,(=\= B1)),
house3:beverage:((=\= B1),(=\= B2))).
clue cons
(house3:beverage:milk, % clue 1
(house1:nationality:spaniard,house1:animal:dog % clue 2
;house2:nationality:spaniard,house2:animal:dog
;house3:nationality:spaniard,house3:animal:dog),
(house1:nationality:ukranian,house1:beverage:tea % clue 3
;house2:nationality:ukranian,house2:beverage:tea
;house3:nationality:ukranian,house3:beverage:tea),
house1:nationality:norwegian, % clue 4
(house1:nationality:norwegian,house2:beverage:tea % clue 5
;house2:nationality:norwegian,house3:beverage:tea
;house2:nationality:norwegian,house1:beverage:tea
;house3:nationality:norwegian,house2:beverage:tea),
(house1:beverage:juice,house1:animal:fox % clue 6
;house2:beverage:juice,house2:animal:fox
;house3:beverage:juice,house3:animal:fox)).
maximality cons
(house1:nationality:(norwegian;ukranian;spaniard), % maximality constraints
house2:nationality:(norwegian;ukranian;spaniard),
house3:nationality:(norwegian;ukranian;spaniard),
house1:animal:(fox;dog;zebra),
house2:animal:(fox;dog;zebra),
house3:animal:(fox;dog;zebra),
house1:beverage:(juice;tea;milk),
house2:beverage:(juice;tea;milk),
house3:beverage:(juice;tea;milk)).
The subsumption hierarchy is shown pictorially in
Figure 4.2. The type, background, with the
assistance of the types subsumed by house and descriptor,
represents the situation: there are three houses (the features of
background), each of which has three attributes (the features of
house). The implicit constraints levied by the situation appear as
constraints on the type, background, namely that no two houses
can have the same value for any attribute. These are represented by
inequations. But notice that, since we are interested in treating the
values of attributes as tokens, we must represent those values by
extensional types. If we had not done this, then we could still, for
example, have two different houses with the beverage, juice,
since there could be two different feature structures of type
juice which were not token-identical. Notice also that all of these
types are maximal, and hence satisfy the restriction that ALE
places on extensional types.
The explicit constraints provided by the clues to the puzzle are represented as constraints on the type clue, a subtype of background. We also need a subtype of clue, maximality, to enforce another constraint implicit to all constraint puzzles, namely the one which requires that we provide only maximally specific answers, rather than vague solutions which say, for example, that the beverage for the third house is a type of beverage ( bev_type), which may actually still satisfy a puzzle's constraints.
To solve the puzzle, we simply type:
| ?- mgsat maximality.
MOST GENERAL SATISFIER OF: maximality
maximality
HOUSE1 house
ANIMAL fox
BEVERAGE juice
NATIONALITY norwegian
HOUSE2 house
ANIMAL zebra
BEVERAGE tea
NATIONALITY ukranian
HOUSE3 house
ANIMAL dog
BEVERAGE milk
NATIONALITY spaniard
ANOTHER? y.
no
| ?-
So the Ukranian owns the zebra, and the Norwegian drinks juice. A
most general satisfier of maximality will also satisfy the
constraints of its supertypes, background and clue.
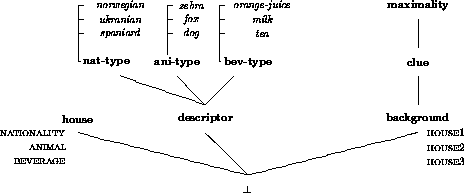
Figure 4.2: Inheritance Network for the Zebra Puzzle.
Although ALE is capable of representing such puzzles and solving them, it is not actually very good at solving them efficiently. To solve such puzzles efficiently, a system must determine an optimal order in which to satisfy all of the various constraints. ALE does not do this since it can express definite clauses in its constraints, and the reordering would also be very difficult for the user to keep track of while designing a grammar. A system which does do this is the general constraint resolver proposed by Penn and Carpenter (1993)
.