|
|
|
|
|
|
|
Master's Thesis
|
|
Indexing and Matching for View-Based
3-D Object Recognition Using Shock Graphs
| Abstract: A shock graph is a shape abstraction that decomposes a shape into hierarchically organized primitive parts. In this thesis, we propose a novel shock graph computation algorithm that yields stable graphs under noise and shape deformation due to viewpoint changes. Next, we extend the indexing and matching framework for hierarchical structures introduced by Shokoufandeh et al., and apply it to the problem of matching shock graphs representing views of 3-D objects. The indexing performance is improved by a vote accumulation algorithm that efficiently solves a multiple one-to-one assignment of votes. In turn, the matching algorithm is extended by ensuring the satisfaction of all the hierarchical constraints encoded in the graphs. We show that the proposed integrated framework is effective in recognizing object shapes and in estimating the pose of their corresponding 3-D object models. We demonstrate the performance of the framework with a database of 2688 object views. |
|
|
The framework
|
|
|
|
|
 |
|
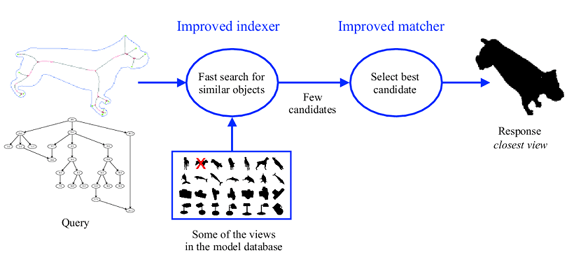
- A query image is represented as a shock graph -- a hierarchical, directed acyclic graph representing the decomposition of a 2-D shape silhouette into primitive parts.
- Given a database of shock graphs representing views of 3-D objects, the shock graph indexing problem is formulated as the selection of a small number of candidate object views from the database that might account for the query.
- In the verification step, each of the candidate shock graphs is matched to the query, yielding a similarity measure that can be used to rank the candidates.
- Finally, the most similar candidate is chosen as the response to the query -- in this case, a novel exemplar is matched to a prototype belonging to the same class.
|
|
|
|
Experiments
- For our experiments we used 21 synthetic objects with128 views per object:
|
|
|
 |
|
|
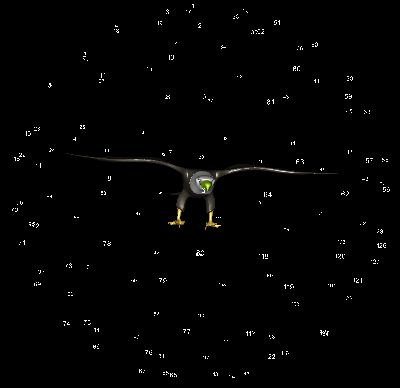
- Shock graphs were computed from regularly tessellated viewing sphere entered around a CAD model of a 3-D object.
|
|
|
 |
|
 |
|
|
 |
|
 |
|
 |
|
 |
 |
 |
|
 |
 |
 |
|
- (left) the eagle's viewing sphere. (right) view #6 of the eagle along with its 9 closest neighbouring views on the sphere.
|
|
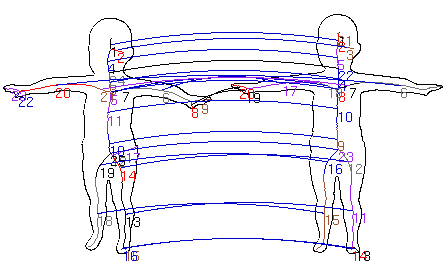
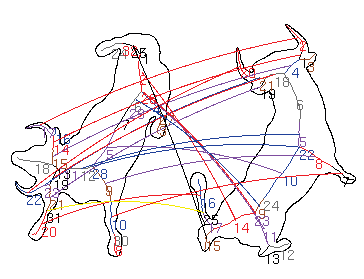
Some Matching Results
|
|
|
 |
 |
|
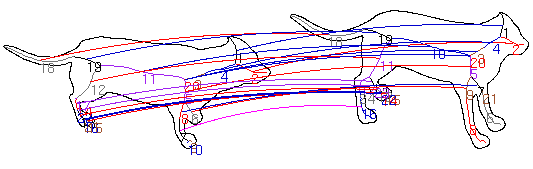 |
|
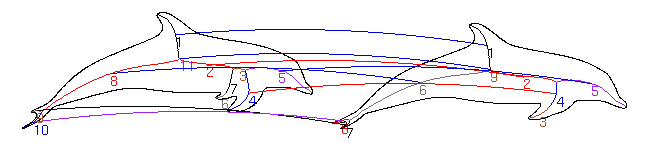 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |

