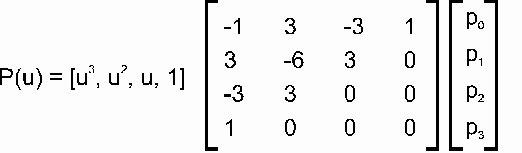La vectorización consiste en representar los contornos obtenidos mediante un conjunto de curvas Bezier. Las curvas Bezier son ampliamente utilizadas en computación gráfica debido a que requieren poco espacio de almacenamiento y son independientes de la resolución de salida que se utilice. Su uso actual se extiende desde la representación de tipografías hasta el modelado de objetos tridimensionales.
Otra ventaja de las curvas Bezier es que permiten hacer cambios locales en la función que representan. Veamos un ejemplo gráfico:
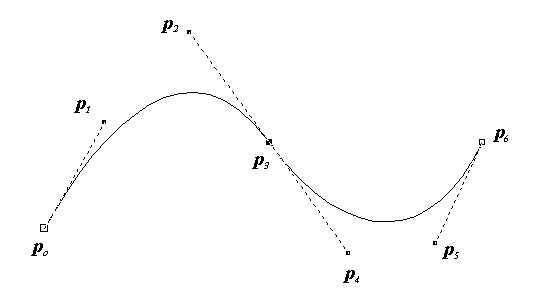
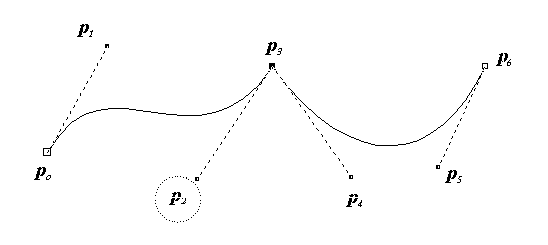
En estos dos gráficos podemos observar como el cambio de un sólo punto, p2, incide únicamente el primer intervalo de la función.
En las curvas Bezier la función no pasa por todos los punto que la definen. Cuatro puntos definen una curva Bezier, pero esta pasa sólo por el primero y último de ellos. Las líneas punteadas que se ven en el gráfico representan la pendiente de la curva, al variar uno de los puntos de una de las líneas punteadas cambia la pendiente y desde luego la forma de la curva. En aplicaciones gráficas se suele ver a las líneas que representan las pendientes como manijas que permiten cambiar la forma de la figura mediante el movimiento de las mismas con un mouse.
Para construir las curvas conviene expresar la función en forma paramétrica. Un punto es el vector pi = (xi, yi)T y el conjunto de punto en forma paramétrica será entonces:
P(u) = ( x(u), y(u) )T, 0 £ u ³ 1.
El polinomio Bezier de grado n determinado por n + 1 puntos se calcula con la formula:
P(u) = S (i=0 a n) ( nCi )( 1 - u )n-i ui pi, donde
( nCi ) = n! / i! ( n- i )!
Con n = 2 nos queda una ecuación cuadrática definida por los puntos p0, p1, p2:
p(u) = (1) (1 - u)2 p0 + 2 (1 - u) (u) p1 + (1) u2 p2
dado que es una representación paramétrica, esta ecuación representa el par de ecuaciones:
x(u) = (1 - u)2 x0 + 2 (1 - u) (u) x1 + u2 x2
y(u) = (1 - u)2 y0 + 2 (1 - u) (u) y1 + u2 y2
Si u = 0, x(0) es idéntico a x0 y lo mismo sucede con y.
Si u = 1, el punto referenciado es (x2, y2).
Si utilizamos un n = 3 obtendremos las denominadas Bezier cubicas. Estas son las generalmente usadas en computación gráfica. En este caso los polinomios tienen la forma:
x(u) = (1 - u)3 x0 + 3 (1 - u)2 u x0 + 3 (1 - u) u2 x1 + u3 x2
y(u) = (1 - u)3 y0 + 3 (1 - u)2 u y0 + 3 (1 - u) u2 y1 + u3 y2
En este caso el punto (x(0), y(0)) = p0 y (x(1), y(1)) = p3
por lo tanto la curva no pasará por los puntos intermedios.