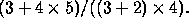
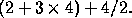 This should be done by giving a screen dump for the original expression and
then additional screen dumps
after repeated uses of the procedure from Part (2c) until the tree
consists of nothing but a value.
This should be done by giving a screen dump for the original expression and
then additional screen dumps
after repeated uses of the procedure from Part (2c) until the tree
consists of nothing but a value.
Parts (2d) and (2e) will constitute the testing part of this assignment.
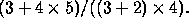
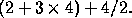 This should be done by giving a screen dump for the original expression and
then additional screen dumps
after repeated uses of the procedure from Part (2c) until the tree
consists of nothing but a value.
This should be done by giving a screen dump for the original expression and
then additional screen dumps
after repeated uses of the procedure from Part (2c) until the tree
consists of nothing but a value.
In this part you are to prove that a recursive procedure is correct.
The Sun newspaper contains puzzles that require the reader to rearrange letters to form a word in English. For example, the letters COHUG could be rearranged into COUGH. Here are some other sets of letters that you can try to rearrange into words: PYGET, HERMY, GINET.
The program in permut.t, shown in figure 4, reads a string and prints all arrangements (actually, all permutations) of it. This program can be used to help a person solve these puzzles. Try running this program with strings such as "abc" to make sure that it prints the permutations (abc, acb, bac, bca, cab and cba). The program is available via showme.

Figure 4: Program for part 3 of the assignment.
You are to prove that the recPermute procedure is correct, using
mathematical induction.
The correctness of the procedure can be stated mathematically, using
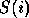 :
:
Your task is to prove that: When recPermute(prefix, T) is called with arbitrary strings prefix and T, where the length of string T is i, the procedure returns after having output the prefix concatenated with every element of PERM(T).
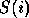 is true for all
is true for all 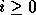 .
.
In proving the correctness of recPermut, you do not need to prove the for-loop is correct. Instead, simply explain precisely what the for-loop accomplishes. That is, give pre- and post-conditions for the for-loop and assume that the for-loop has been proven correct with respect to them.
In your proof, you can use this definition of the ``set of permutations of string T'':
The set of permutations of a given string T is defined as: the null string if T is the null string; otherwise it is the set of strings obtained by concatenating to each character in T every permutation of the remaining characters of T.
The files for this assignment can be picked up from a directory in the CDF PC labs as follows:
n:\
csc148h.
a4.
The folder corresponding to a4 should be
highlighted and the files displayed in the accompanying panel.
h:\
and confirm (click on OK) until finished.
h:\a4\ which
contains all the files for a4.
Within WinOOT, you can click on
the a4 folder and complete the assignment.
Screen dumps can be done in the CDF PC lab by typing Control-P after selecting the window you want printed. To select a window, move the cursor into the window and click. Please be sparing with your use of the printer.
University of Toronto
csc148 -- Introduction to
Computer Science, Fall 1995
Complete this page, and tape it to the front of the envelope containing your assignment.
