Lecture 07: Recursive Correctness
2025-07-02
I’m trying something different for today’s lecture. These are the reference slides, but I’ll be lecturing off of some more bare-bones slides using my iPad. I feel like I draw more freely on the iPad and have been feeling a bit constrained by the slides.
Recap
Last time, we saw some new methods for solving recurrences.
- Substitution method
- Recursion tree (for intuition)
- Master Theorem
Algorithm Correctness
Algorithm Correctness
Today, we will see how to prove algorithms are “correct”.
What does it mean for an algorithm to be correct?
Correctness (formally)
For any algorithm/function/program, define a precondition and a postcondition.
The precondition is an assertion about the inputs to a program.
The postcondition is an assertion about the end of a program.
An algorithm is correct if the precondition implies the postcondition.
I.e. “If I gave you valid inputs, your algorithm should give me the expected outputs.”
This is essentially a design specification.
Documentation Analogy
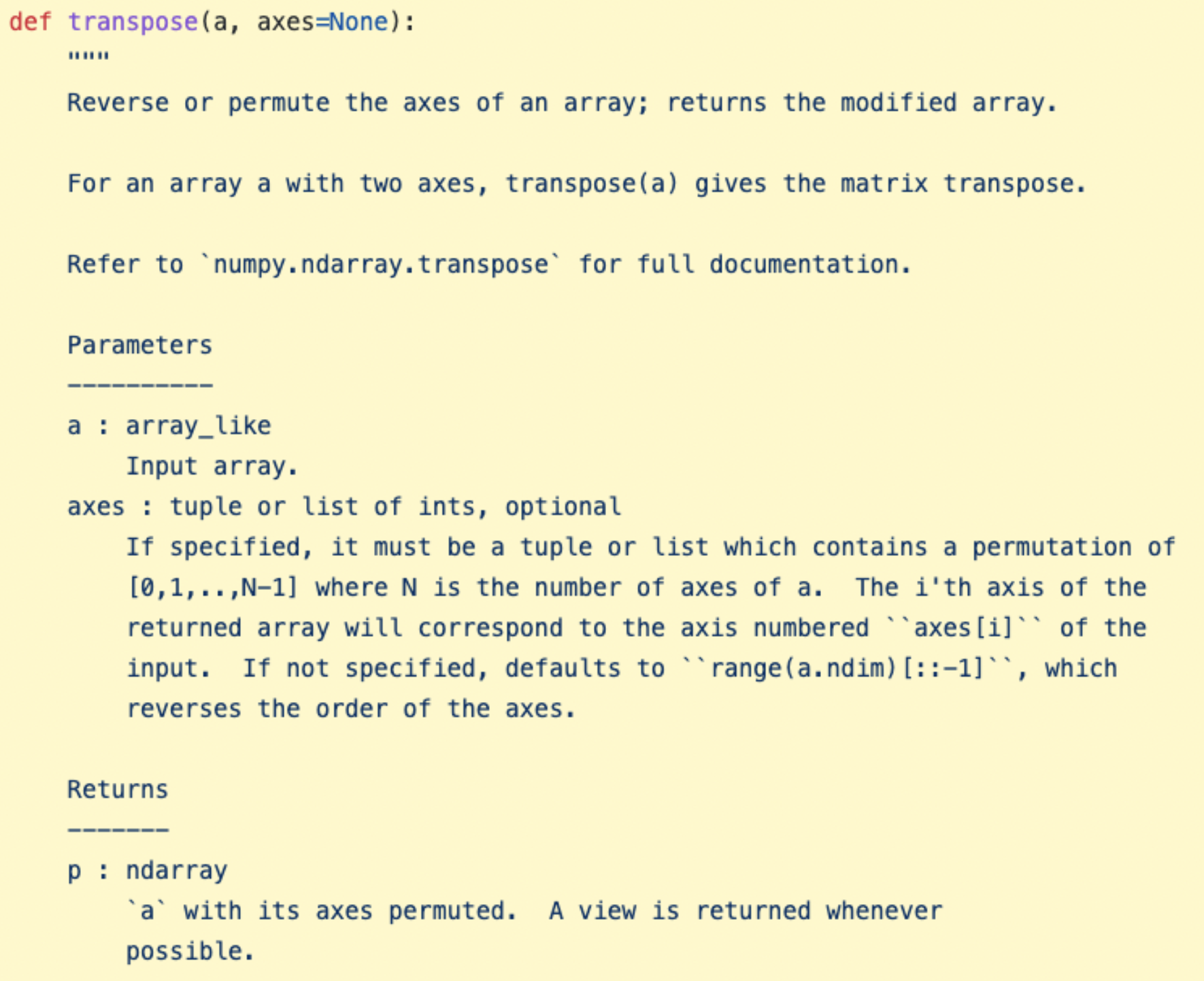
What is the pre/post conditions for mergesort\((l)\)?
Solution
Precondition: \(l\) should be a list of natural numbers.
Postcondition: The return value of \(\texttt{mergesort}\) should contain the elements of \(l\) in sorted order.
What is the pre/post condition for \(\texttt{binsearch}(l, t, a, b)\)?
Solution
Precondition: \(l \in \texttt{List}[\mathbb{N}]\), \(l\) is sorted, \(t, a, b \in \mathbb{N}\), \(a, b \leq \texttt{len}(l)\).
Postcondition: If \(t\) is in \(l[a:b]\) return the index of \(t\) in \(l\), otherwise, return \(\texttt{None}\).
How do you prove correctness for recursive functions?
By induction on the size of the inputs!
Notation
Let’s use CS/Python notation. I.e., the elements of a list of length \(n\) in order are \(l[0],l[1],...,l[n-1]\).
Slicing: \[ l[i:j] = [l[i],l[i+1],...,l[j-1]] \]
By convention, if \(j \leq i\), then \(l[i:j] = []\).
Conventions
Today, let’s think of all lists as being lists of natural numbers.
Correctness - Merge Sort
Merge Sort
Merge Sort - Correctness
As usual, we break this down and show for all \(n \in \mathbb{N}\), if \(l \in \texttt{List}[\mathbb{N}]\) is a list of length \(n\), then \(\texttt{mergesort}\) works on \(l\).
Correctness
\(P(n)\): Let \(l \in \texttt{List}[\mathbb{N}]\) be a list of natural numbers of length \(n\), then \(\texttt{mergesort}(l)\) returns the sorted list.
Claim: \(\forall n \in \mathbb{N}.(P(n))\).
Correctness of Merge
For now, let’s assume \(\texttt{merge}\) is correct. I.e. that on sorted lists \(\texttt{left}\) and \(\texttt{right}\), \(\texttt{merge}(\texttt{left}, \texttt{right})\) returns a sorted list containing all the elements in either list.
We’ll come back and prove that later!
Base case
Solution
Let \(l\) be a list of length \(0\) or \(1\). Note that \(l\) is already sorted. In this case, \(\texttt{mergesort}(l)\) returns \(l\) as expected.Inductive step
Solution
Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume for all \(i \in \mathbb{N}\) with \(0 \leq i \leq k\), \(\texttt{mergesort}\) works on lists of length \(i\). We’ll show that \(\texttt{mergesort}\) also works on lists of length \(k + 1\). Let \(l\) be a list of length \(k+1\).
Since \(k + 1 \geq 2\), we fall into the else case. The left sublist is a list of length \(\left\lfloor (k+1)/2 \right\rfloor\). We have \[ \begin{align*} \left\lfloor (k+1)/2 \right\rfloor & \leq (k+1)/2 \\ & \leq (k+k)/2 & (k \geq 1) \\ & \leq k \end{align*} \]
Thus, by the inductive hypothesis, \(\texttt{mergesort}\) correctly sorts the left sublist, and \(\texttt{left}\) contains the sorted left sublist.
The right sublist is a list of length \(\left\lceil (k+1)/2 \right\rceil\). Since \(k \geq 1\), \(\left\lceil (k+1)/2 \right\rceil \leq \left\lceil (k+k)/2 \right\rceil = k\).
Thus, by the inductive hypothesis, \(\texttt{mergesort}\) correctly sorts the right sublist, and \(\texttt{right}\) contains the sorted right sublist.
Since we’re assuming that \(\texttt{merge}\) works, and \(\texttt{left}\), and \(\texttt{right}\) are sorted lists, and \(\texttt{l}\) is composed of the elements in \(\texttt{left}\) and \(\texttt{right}\), we return \(\texttt{merge}(\texttt{left}, \texttt{right})\) which is the sorted version of \(l\).
Notes
The fact that the algorithm terminates (i.e. doesn’t get stuck in an infinite loop) is implied by the statement of the claim in the word returns.
Multiplication
Recursive Algorithms
This next example will put together what we have studied so far on recursive runtime and correctness.
Multiplication
Let’s study multiplication!
If I gave you two 10 digit numbers, how would you multiply them?
Grade School Multiplcation
Lower bound for the Grade School Multiplcation Algorithm
Suppose I gave you two \(n\)-digit numbers. What is a lower bound for the runtime of the Grade School Multiplication Algorithm?Solution
\(n^2\). For each digit of the second number, I need to multiply it with every digit of the first number.Can we do better?
Karatsuba’s Algorithm
def karatsuba(x, y):
if x < 10 and y < 10:
return x * y
n = max(len(str(x)), len(str(y)))
m = n//2
x_h = x // 10**m
x_k = x % 10**m
y_h = y // 10**m
y_l = y % 10**m
z_0 = karatsuba(x_l, y_l)
z_1 = karatsuba(x_l + x_h, y_l + y_h)
z_2 = karatsuba(x_h, y_h)
return (z_2 * 10**(2*m)) + ((z_1 - z_2 - z_0) * 10**m) + z_0x // 10**m, and x % 10**m?
Solution
the first \(\left\lceil n/2 \right\rceil\), and last \(\left\lfloor n/2 \right\rfloor\) digits of \(x\).Trace the algorithm by hand on inputs \(a = 31\) and \(b = 79\), report the values of each of the variables \(m,x_l,x_h,y_l,y_h,z_0,z_1,z_2\) as well as the result.
Write a recurrence for the runtime of Karatsuba’s algorithm. Solve the recurrence.Solution
\(T(n) = 3T(n/2) + n\), which is \(\Theta(n^{\log_3(2)})\) by the Master Theorem - this is asymptotically better than the Grade School Algorithm!Correctness
Precondition. \(x, y \in \mathbb{N}\), Postcondition. Return \(xy\)
\(m = \left\lfloor n/2 \right\rfloor\), \(x_h = \left\lfloor x/10^m \right\rfloor\), \(x_l = x \% 10^m\)
\(z_0 = x_ly_l\), \(z_1 = (x_l + x_h)(y_l + y_h)\), \(z_2 = x_hy_h\)
return\((z_2 \cdot 10^{2m}) + ((z_1 - z_2 - z_0) \cdot 10^{m}) + z_0\)
Solution
If \(\max(x, y) = n\), then \(\texttt{karat}(x, y)\) returns \(xy\). We’ll show \(\forall n \in \mathbb{N}, n \geq 1. P(n)\)Solution
We will show \(P(0),...,P(9)\) In these cases, both \(x\) and \(y\) are a single digit and we enter the base case and return \(xy\) as required.Solution
Let \(k\) be an arbitrary natural number with \(k \geq 10\), and suppose \(P(0),...,P(k-1)\). We’ll show \(P(k)\). To apply the inductive hypotheses to the recursive calls, we need \(x_h, x_l, y_h, y_l, x_h+x_l, y_h + y_l\) to all be \(<k\). Since \(k \geq 10\), we have that \(m \geq 1\).
Since \(x \leq k\), and \(x = x_h10^m + x_l\), we have \(x_h + x_l < k\). Additionally, since \(x_h, x_l\) are non-negative, they must also be individually less than \(k\). Same for \(y_h\) and \(y_l\). Thus, the inductive hypothesis applies to the recursive calls, and \(z_0, z_1, z_2\) contain the correct products.
Then, the return value is
\[ \begin{align*} & (z_2 \cdot 10^{2m}) + ((z_1 - z_2 - z_0) \cdot 10^{m}) + z_0 \\ & =x_hy_h10^{2m} + ((x_h+x_l)(y_l+y_h) -x_hy_h-x_ly_l)\cdot 10^m + x_ly_l \\ & =x_hy_h10^{2m} + (x_hy_l + y_hx_l)\cdot 10^m + x_ly_l \\ & =(x_h10^{m} + x_l)(y_h10^{m} + y_l) \\ & =xy \end{align*} \]
An alternate \(P(n)\)
Instead of letting \(n\) be the maximum value of \(x\) and \(y\), could we have set \(n\) to be the maximum length of \(x\) and \(y\)?Solution
You will run into trouble in the inductive step. For example if \(x = 99\), then \(x_l = x_h = 9\), which have fewer digits, but \(x_l + x_h = 18\) which is still 2 digits long so you can’t use the inductive hypothesis! You can fix this by extending the base case to \(3\), but this is more work!Summary: Correctness for Recursive Algorithms
Prove the correctness of recursive algorithms by induction. The link between recursive algorithms and inductive proofs is strong.
The base case of the recursive algorithm corresponds to the inductive proof’s base case(s).
The recursive case of the recursive algorithm corresponds to the inductive step.
The ‘leap of faith’ in believing that the recursive calls works correspond to the inductive hypothesis.
Correctness - Binary Search
Binary Search

Correctness Claim: First attempt
\(P(n)\): If \(l \in \texttt{List}[\mathbb{N}]\) is a list of length \(n\), binsearch\((l, t, a=0, b=n)\) returns the index of \(t\) if \(t\) is in \(l\) and \(\texttt{None}\) otherwise.
Claim: for all \(n \in \mathbb{N}.(P(n))\).
Base case
Consider the \(n = 0\) case. let \(l\) be any list of length \(0\), \(t\) be any object, and consider binsearch\((l, t, 0, 0)\).
The check \(\texttt{a==b}\) is true since both variables are \(0\) so we return \(\texttt{None}\). This is the expected result since an empty list surely does not contain \(t\).
Inductive Step
Let \(k \in \mathbb{N}\) and assume for all \(i \in \mathbb{N}, i \leq k\), binsearch\((l, t, 0, i)\) returns the desired result for all lists of length \(i\).
Let \(l \in \texttt{List}[\mathbb{N}]\) be a list of length \(k+1\), and let \(t \in \mathbb{N}\). Consider the execution of binsearch\((l, t, 0, k+1)\). Since \(k + 1 \geq 1\), the if condition fails. Let \(m = (k+1)//2 = \left\lfloor (k+1)/2 \right\rfloor\) There are then 3 cases.
Case 1. \(\texttt{l[m]} == \texttt{t}\).
Case 2. \(\texttt{l[m]} < \texttt{t}\).
Case 3. \(\texttt{l[m]} > \texttt{t}\).
Case 1. \(\texttt{l[m]} == \texttt{t}\)
In this case \(\texttt{binsearch}\) returns \(m\), which is indeed the index of \(t\) in \(l\).
Case 2. \(\texttt{l[m]} < \texttt{t}\)
In this case, we return \(\texttt{binsearch}(l, t, m+1, k+1)\). ...
Here was our inductive hypothesis.
Let \(k \in \mathbb{N}\) and assume for all \(i \in \mathbb{N}, i \leq k\), binsearch\((l, t, 0, i)\) returns the desired result for all lists of length \(i\).
The inductive hypothesis doesn’t apply here! Since \(a \neq 0\)!
How can we fix it?
A fix that doesn’t quite work
Instead of calling \(\texttt{binsearch}(l, t, m+1, k+1)\) make the recursive call
\[ \texttt{binsearch}(l[m+1:k+1], t, 0, k+1) \]
Why doesn’t this work?
The index of \(t\) in \(l[m+1:k+1]\) is different from the index of \(t\) in \(l\)!
Correctness Claim, Corrected
Instead of doing induction on the length of the list, do induction on the length of the search window!
\(P(n)\): For all lists \(l \in \texttt{List}[\mathbb{N}]\) and \(t \in \mathbb{N}\), if \(b-a = n\), then \(\texttt{binsearch}(l, t, a, b)\) returns \(\texttt{None}\) if \(t\) is not in \(l[a:b]\) and the index of \(t\) in \(l\) otherwise.
Claim: \(\forall n\in \mathbb{N}. P(n)\).
Solution
Base Case. Let \(l\) be any list and \(t\) suppose \(b - a = 0\). Then \(l[a:b] = []\), so \(t\) can is not in \(l\) and we expect the algorithm to return \(\texttt{None}\).
Indeed, since \(\texttt{b == a}\), the first if check passes and \(\texttt{binsearch}(l, t, a, b)\) returns \(\texttt{None}\).
Inductive Step.
Let \(k \in \mathbb{N}\) with \(k \geq 1\), and assume for all \(i \in \mathbb{N}\), \(i < k\), \(P(i)\). We’ll show \(P(k)\). Let \(l \in \texttt{List}[\mathbb{N}]\) be a sorted list, and \(t, a, b, \in \mathbb{N}\) such that \(b - a = k\).
We’ll show that \(\texttt{binsearch}(l, t, a, b)\) returns \(\texttt{None}\) if \(t\) is not in \(l[a:b]\) and the index of \(t\) in \(l\) otherwise
Since \(b - a = k \geq 1\), the first if check fails. Let \(m = \texttt{(a + b)//2} = \left\lfloor (a + b)/2 \right\rfloor\). There are then 3 cases.
l[m] == t
In this case, the algorithm returns \(m\), which is the index of \(t\) in \(l\).
To prove the exact form of the statement, we need to check that \(l[m] = t\) is actually in \(l[a: b]\). I.e. that \(a \leq m \leq b-1\).
We have \[ \begin{align*} m & = \left\lfloor (a + b)/2 \right\rfloor \\ & \geq \left\lfloor (2a + 1)/2 \right\rfloor & (b - a \geq 1) \\ & \geq \left\lfloor a + (1/2) \right\rfloor \\ & \geq a \end{align*} \]
On the other side, we have
\[ \begin{align*} m & = \left\lfloor (a + b)/2 \right\rfloor \\ & \leq \left\lfloor (2b - 1)/2 \right\rfloor & (b - a \geq 1) \\ & \leq \left\lfloor b - (1/2) \right\rfloor \\ & = b-1 \end{align*} \]
l[m] < t
Since \(l\) is sorted and \(t\) is greater than the \(l[m]\), if \(t\) is to be in \(l[a:b]\), it must have an index greater than \(m\). So \(\texttt{binsearch}(l, t, a, b) = \texttt{binsearch}(l,t, m+1, b)\).
We claim that our inductive hypothesis applies to \(\texttt{binsearch}(l, t, m+1, b)\). We just need to show \(b-(m+1) < k\).
WTS: \(b-(m+1) \leq k\). From the previous part, we know that \(m \geq a\).
l[m] > t
Since \(l\) is sorted and \(t\) is less than the \(l[m]\), if \(t\) is to be in \(l[a:b]\), it must have an index less than \(m\). So \(\texttt{binsearch}(l, t, a, b) = \texttt{binsearch}(l,t, a, m)\).
We claim that our inductive hypothesis applies to \(\texttt{binsearch}(l, t, a, m)\). We need to show \(m-a \leq k\).
WTS: \(m-a \leq k\). From the previous part, we have \(m \leq b - 1\).
Then \(m - a \leq b-1-a \leq k-1\), so the inductive hypothesis holds for \(\texttt{binsearch}(l, t, a, m)\), and we are done!
CSC236 Summer 2025