Lecture 04: Induction 2

2025-05-28

While we wait…

Discuss with the person next to you: What is your favorite algorithm or theorem?

Recap

Announcement: Tutorial today

If you’re in TUT5103 or 5101, please go to BA1200 for tutorial instead of your usual rooms (BA B024 or 2139).

If you’re in one of the the other tutorials, please go to your usual rooms.

Induction and Complete Induction

To prove \[ \forall n \in \mathbb{N}. (P(n)) \]

it is enough to prove $P(0)$ and one of the following

$\forall k \in \mathbb{N}. [P(k) \implies P(k+1)]$
$\forall k \in \mathbb{N}. [(P(0) \land P(1) \land ... \land P(k)) \implies P(k+1)]$

Intuition: why does (regular) induction work again?

Say I managed to show $P(0)$, and $\forall k \in \mathbb{N}. (P(k) \implies P(k+1))$. Then let $n \in \mathbb{N}$ be any number, here’s why $P(n)$ is true:

$P(0) \implies P(1)$, and $P(0)$, so $P(1)$
$P(1) \implies P(2)$, and $P(1)$, so $P(2)$
...
$P(n-1) \implies P(n)$, and $P(n)$, so $P(n)$.

Intuition: why does (complete) induction work again?

Say I managed to show $P(0)$, and $\forall k \in \mathbb{N}. ((P(0)\land P(1) \land ... P(k)) \implies P(k+1))$. Then let $n \in \mathbb{N}$ be any number, here’s why $P(n)$ is true:

$P(0) \implies P(1)$, and $P(0)$, so $P(1)$
$P(0) \land P(1) \implies P(2)$, and $P(0) \land P(1)$, so $P(2)$
...
$(P(0) \land .... \land P(n-1)) \implies P(n)$, and $P(0) \land ... \land P(n-1)$, so $P(n)$.

Postage Stamps

Say that you have an unlimited number of 3 cent and 5 cent postage stamps. Can you make any postage exactly?

No, i.e. 1, 2, 4, 7 can’t be made.

Can you make any postage $\geq 8$ cents exactly?

Rephrasing the problem mathematically

Claim: For any $n \geq 8$, there exists $a, b \in \mathbb{N}$ such that $n = 3a + 5b$.

Proof, attempt 1 (wrong!)

Claim: For any $n \geq 8$, there exists $a, b \in \mathbb{N}$ such that $n = 3a + 5b$

By complete induction.

Base case. We can make an $8$ cent postage using one $3$ cent stamp and one $5$ cent stamp.

Inductive step. Let $k \geq 8$ and assume for any $8 \leq i \leq k$, we can make a postage of $i$ cents using only 3 and 5 cent stamps. We’ll show that you can also make a $k+1$ postage. Use one 3-cent stamp. We now need to make a $k-2$ postage. By the induction hypothesis, we can make $k-2$ using only $3$ cent and $5$ cent stamps, so together, we have made a $k+1$ postage.

What’s the problem here?

Solution

$k-2$ might be $6$ which is not covered by the induction hypothesis

Problem

Our induction hypothesis was $P(8),P(9),...,P(k)$, and we wanted to show $P(k+1)$. However, when $k = 8$ or $9$, $k-2$ is $6$ or $7$ which is not covered by the induction hypothesis! So our argument in the inductive step doesn’t work for $k=8$ or $k=9$.

To fix this, we can just prove $P(k+1)$ directly for these cases for $k=8$ and $k=9$.

Proof 1. multiple base cases

Claim: For any $n \geq 8$, there exists $a, b \in \mathbb{N}$ such that $n = 3a + 5b$

Solution

By complete induction.

Base cases. Since $8 = 3 + 5, 9=3 + 3+3, 10 = 5 +5$, we can make postages of $8, 9, 10$.

Inductive step. Let $k \geq 10$ and assume for any $8 \leq i \leq k$, we can make a postage of $i$ cents using only 3 and 5 cent stamps. We’ll show that you can also make a $k+1$ postage. Use one 3 cent stamp, we now need to make a $k-2$ postage. Since $8 \leq k-2$, the induction hypothesis applies, and we can make $k-2$ using only $3$ cent and $5$ cent stamps, so together, we have made a $k+1$ postage.

Proof 2. Regular induction

Claim: For any $n \geq 8$, there exists $a, b \in \mathbb{N}$ such that $n = 3a + 5b$

Solution

By regular induction.

Base case. Same as before

Inductive step. Let $k \geq 8$, and assume there are $a, b \in \mathbb{N}$ such that $k = 3a + 5b$. There are two cases

If $b \geq 1$, we can create $k+1$ by removing a 5 cent stamp and adding two 3 cent stamps.
If $b = 0$, then since $k \geq 8$, $a \geq 3$, and we can create $k+1$ by removing three 3 cent stamps and adding two 5 cent stamps.

Structural Induction

Induction

So far, we’ve been able to use the powerful tools of induction and complete induction to prove statements of the form. \[ \forall n \in \mathbb{N}. (P(n)). \] However, in life, we are also interested in objects other than the natural numbers. For example, lists, trees, and logical formulas. I.e., we may want to prove statements like \[ \forall \mathrm{Trees }T. (P(T)), \]

and

\[ \forall \mathrm{Formulas } f . (P(f)). \]

We “need”¹ a more general tool.

Another view of $\mathbb{N}$

Here’s another one way to define $\mathbb{N}= \{0,1,2,...\}$. Let $\mathrm{AddOne}$ be the function that maps $x \to x+1$.

Then, $\mathbb{N}$ is the set of objects can be reached by applying $\mathrm{AddOne}$ to $\{0\}$ a finite number of times.

Defining Sets Inductively

Let $B \subseteq U$ (think $B$ for base cases)
Let $F$ be a set of functions, where each function $f \in F$ has domain $U^m$ and codomain $U$. I.e. $f$ maps a tuple of elements of $U$ to a single element of $U$ (think of $F$ as a set of construction operations)

The set generated from $B$ by the functions in $F$ is the set of elements that can be obtained by applying functions in $F$ to elements of $B$ a finite number of times.

Alternatively

An equivalent way to express

“$A$ is the set of elements that can be obtained by applying functions in $F$ to elements of $B$ a finite number of times.”

is to define

$A$ is the smallest set satisfying the following conditions.

$B \subseteq A$
$\forall a \in A, f \in F$, $f(a) \in A$.

Example: $\mathbb{N}$

$B = \{0\}$
$F = \{\mathrm{AddOne}\}$

$\mathbb{N}$ is the set generated from $\{0\}$ by $\{\mathrm{AddOne}\}$
Alternatively, $\mathbb{N}$ is the smallest set that contains $0$, and for each $n \in \mathbb{N}$, $\mathbb{N}$ also contains $\mathrm{AddOne}(n)$.

Example: $\mathbb{Z}$

$\mathbb{Z}$ is the set generated from $\{0\}$ by $\{\mathrm{AddOne}, \mathrm{MinusOne}\}$
Alternatively, $\mathbb{Z}$ is the smallest set that contains $0$, and for each $z \in \mathbb{Z}$, $\mathbb{Z}$ also contains $\mathrm{AddOne}(z)$, and $\mathrm{MinusOne}(z)$.

Example: $\texttt{List}[X]$

Let $X$ be some set, and let $\texttt{List}[X]$ be the set of lists whose entries are in $X$.

For example, $[1, 2, 4, 2] \in \texttt{List}[\mathbb{N}]$, and $[\text{'cat'}, \text{'dog'}] \in \texttt{List}[\texttt{Strings}]$.

For each $x \in X$ define the function $\mathrm{Append}_x$ be the function that takes in a $l$ and appends $x$ to $l$.

$B = \{[]\}$
$F = \{\mathrm{Append}_x: x \in X\}$

$\texttt{List}[X]$ is the set generated from $B$ by functions in $F$.

Propositional logic

Propositional logic is logic without predicates or quantifiers. For example $((A \land B) \lor (\neg C))$ is a propositional formula. Let $\mathrm{Prop}$ be the set of propositional formulas. Define $\mathrm{Prop}$ inductively.

$B = \{A, B, C,...\}$ be a set of variables
$F = \{\mathbf{E}_\neg, \mathbf{E}_\land, \mathbf{E}_\lor\}$

Where $\mathbf{E}_\neg(A) = (\neg A)$, $\mathbf{E}_\land(A, B) = (A \land B)$, and $\mathbf{E}_\lor(A, B) = (A \lor B)$.

Structural Induction

Let $P$ be any predicate.

If I can show $P$ is true of all the base cases,
and I can show that for every construction function, if $P$ holds for the the inputs to the construction function then $P$ must hold for the output of the construction function,

Then $P$ holds for every element constructed from the bases cases and the construction functions.

Structural Induction (Formally)

Let $C$ be a set generated from $B$ by the functions in $F$. If

for every $b \in B$, $P(b)$,
and for every $f \in F$ on $m$ inputs, for every $a_1,...,a_m \in C$, $(P(a_1)\land P(a_2) \land ... \land P(a_m)) \implies P(f(a_1,...,a_m))$

Then $\forall x \in C. (P(x))$

Recovering regular induction

Let $C$ be a set generated from $B$ by the functions in $F$. If

for every $b \in B$, $P(b)$,
and for every $f \in F$ on $m$ inputs, for every $a_1,...,a_m \in C$, $(P(a_1)\land P(a_2) \land ... \land P(a_m)) \implies P(f(a_1,...,a_m))$

Then $\forall x \in C. (P(x))$

$\mathbb{N}$ is generated by $\{0\}$ and $\mathrm{AddOne}$.

So substitute $\mathbb{N}$ for $C$, $\{0\}$ for $B$ and $\{\mathrm{AddOne}\}$ for $F$.

Flexibility

This more general version formalizes the intuition for why were were able to change the base cases when trying to prove, for example, $\forall n \in \mathbb{N}, n \geq 4. (P(n))$.

We really just showed $P$ holds for every number in the set $\mathbb{N}_{\geq 4} = \{4, 5, 6,...\}$ which is generated from the singleton set $\{4\}$, and the function $\mathrm{AddOne}$.

Perfect Binary Trees (Again)

Last time we showed a perfect binary tree of height $h$ has $2^{h+1} - 1$ vertices. By showing $2^0 + 2^1 + ... + 2^{h} = 2^{h+1} - 1$ for all $h \in \mathbb{N}$.

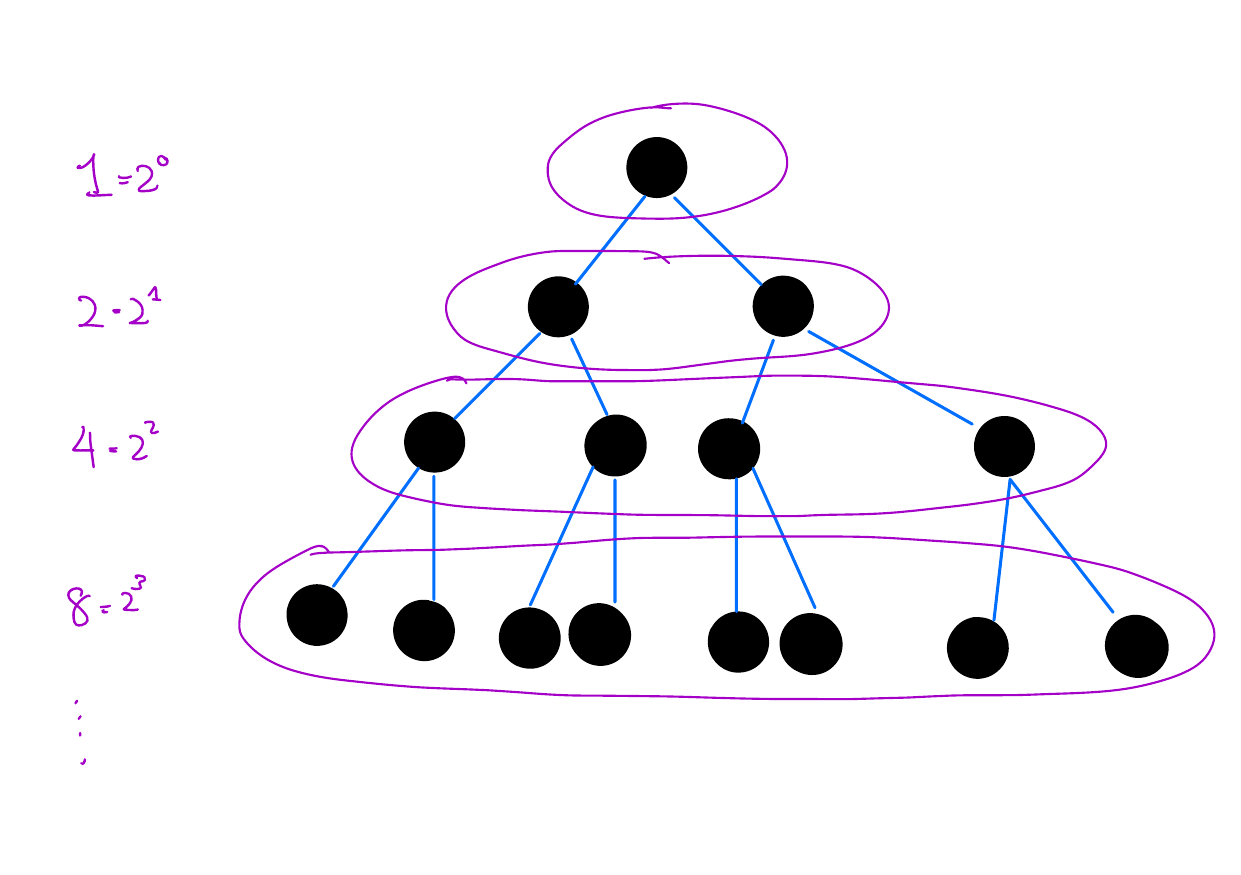
An alternate way of looking at things

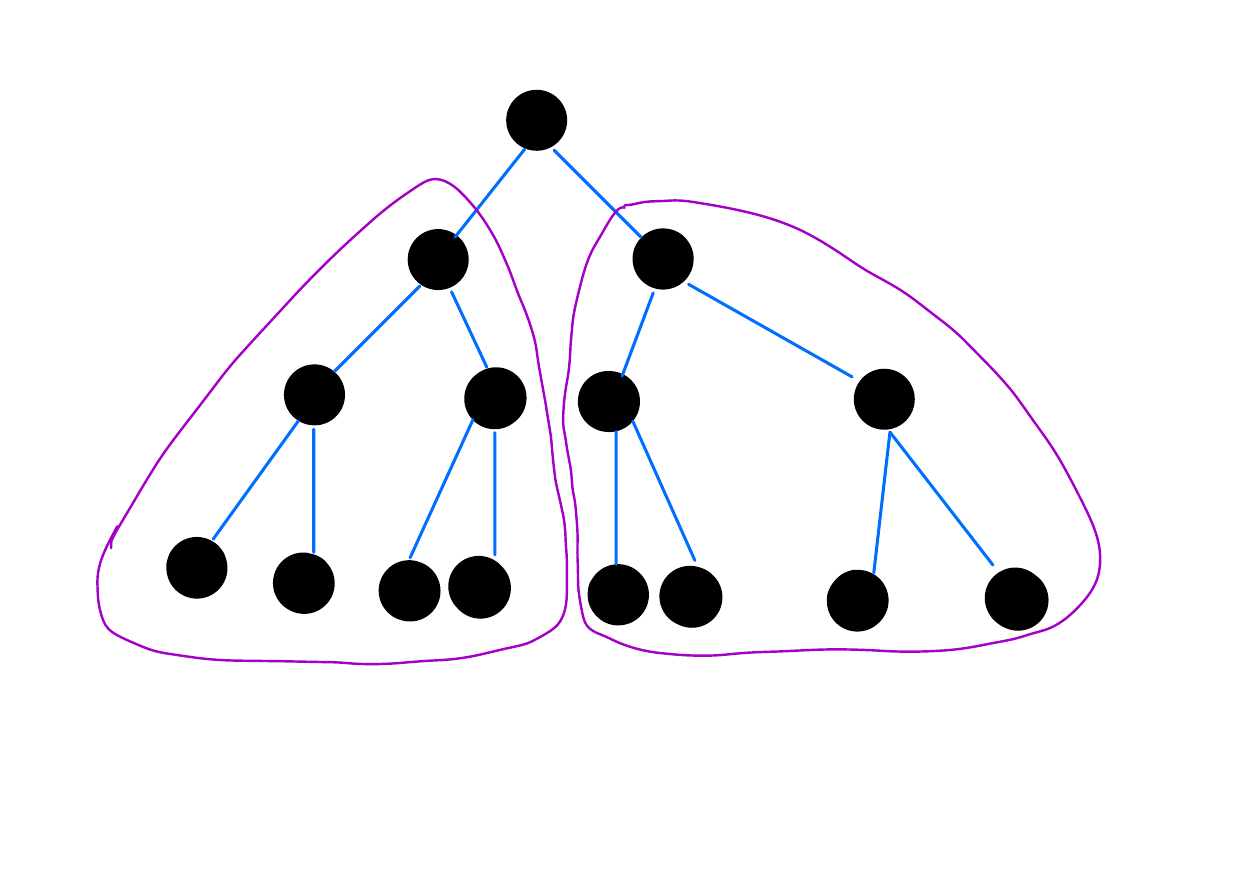
Perfect Binary Trees

Let $\mathrm{PerfectBinaryTrees}$ be the set of perfect binary trees, and let’s write it as being generated from a set by some function.

$U$ (for example might be the set of all graphs).
$B = \{\text{single node}\}$
$\mathrm{JoinPerfectTrees}: U \times U \to U$ maps $(G_1, G_2)$ to the tree with $G_1$ as left subtree and $G_2$ as right subtree if and only if $G_1$ and $G_2$ are perfect binary trees of the same height. Otherwise, map to the graph with a single node.

$\mathrm{JoinPerfectTrees}$

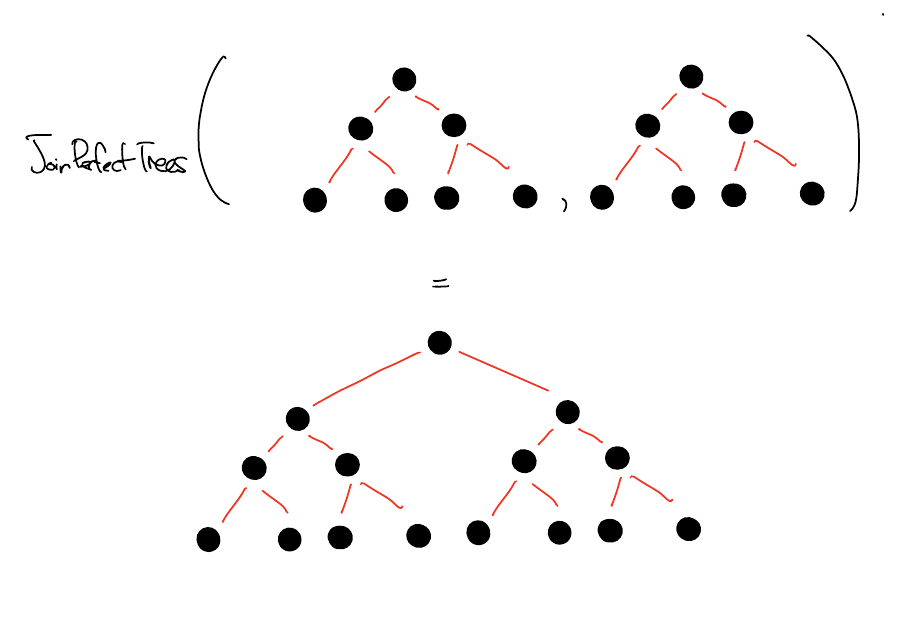
A perfect binary tree of height $h$ has $2^{h+1} - 1$ vertices

Solution

Let $P(G)$ be the predicate that if $G$ is a perfect binary tree of height $h$, then $G$ has $2^{h+1} - 1$ vertices.

By structural induction.

Base case. The base case is the graph consisting of a single node. It has height 0 and $2^{0 + 1} - 1 = 1$ vertices so the base case is true.

Inductive step. Let $G_1 = (V_1, E_1), G_2 = (V_2, E_2)$ be perfect binary trees and assume $P$ holds for $G_1$ and $G_2$. We’ll show that $P$ also holds for $\mathrm{JoinPerfectTrees}(G_1, G_2)$.

Note that if $G_1$ and $G_2$ not are of the same height $h$, $\mathrm{JoinPerfectTrees}(G_1, G_2)$ is the single node graph, which is just the base case. Otherwise, $G_1$ and $G_2$ are both perfect binary trees of the same height $h$. By the induction hypothesis, $|V_1| = |V_2| = 2^{h+1} - 1$. $\mathrm{JoinPerfectTrees}(G_1, G_2)$ is then a perfect binary tree of height $h+1$ with \[ \begin{align*} 1 + 2(2^{h+1} - 1) & = 2^{h+2} - 1 \end{align*} \]

vertices as required.

Postage Stamps (Again)

Solution

By structural induction.

$\mathbb{N}_{\geq 8}$ is generated by $\{8, 9, 10\}$ and $\{\mathrm{Add3}\}$. (You need to justify this part...)

Base Case. You can make $8 = 3 + 5$, $9 = 3\cdot 3$, $10 = 5 \cdot 2$.

Inductive Step. Let $k \in \mathbb{N}_{\geq 8}$, and assume $k = 3a + 5b$ for some $a, b \in \mathbb{N}$. Then $\text{Add3}(k) = k+3 = 3a + 5b + 3 = 3(a+1) + 5b$.

Structural vs. Complete Induction

If you prefer complete induction to structural induction, you can always opt to use complete induction instead. The following slides will detail why.

Construction Sequences

Let $C$ be the set generated from $B$ by the functions in $F$. Define a construction sequence of length $n$, to be a sequence of elements $(x_0,..,x_n)$ where for each $x_i$ in the sequence, either

$x_i \in B$,
or $x_i = f(x_{j_1},...,x_{j_m})$ for some $f \in F$, and $j_1,...,j_m < i$.

I.e., every element in the sequence is either in the base set $B$ or is constructed by applying a construction function to earlier elements in the sequence.

Example - construction sequence

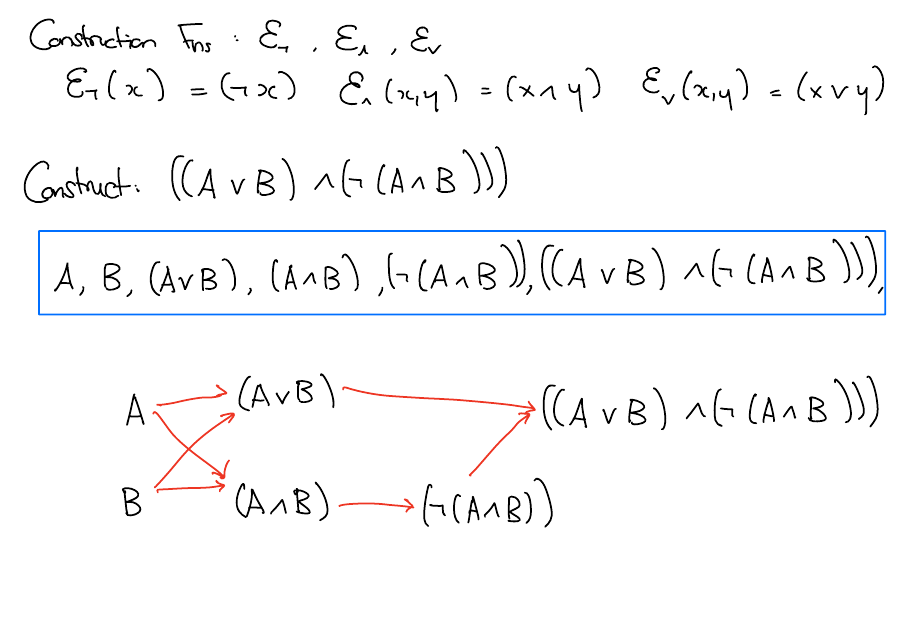
Structural vs. Complete Induction

Define $C_i$ be the set where $x \in C_i$ if there exists some construction sequence of length at most $i$ ending in $x$. Then $C = C_0 \cup C_1 \cup ...$.

Instead of doing structural induction, we can do induction on the length of the construction sequence. I.e., show that if $P$ holds for every element with construction sequences of at most $k$, then $P$ also holds for elements with construction sequences of length at most $k+1$.

Usually, length of construction sequence is represented by some measure of complexity of the object, for example, ‘height of a tree’ or ‘number of parenthesis,’ or ‘length of the list.’

Perfect Binary Trees (again again)

Solution

Claim. A perfect binary tree of height $h$ has $2^{h+1} - 1$ vertices.

Base case. A perfect binary tree of height $0$ has $2^{0+1} - 1 = 1$ vertices so the base case holds.

Inductive step. let $k \in \mathbb{N}$ be any natural number and assume perfect binary trees of height $k$ have $2^{k+1} - 1$ vertices. Let $T$ be a perfect binary tree of height $k+1$. Note that $T$ is constructed of an additional node joining two perfect binary trees of height $k$. Thus $T$ has $2(2^{k+1} - 1) + 1 = 2^{k+2} - 1$ vertices as required.

Note: Here, we used the tree’s height as a proxy for the length of the construction sequence.

Level of Formality

So far, we have seen many examples of proof by induction. You can use any approach you wish.

You don’t need to talk about construction sequences in your proofs and can instead say, for example, ‘by induction on the height of the tree.’

Structural induction is usually trickier to get right, so I’d recommend sticking to complete/regular induction whenever possible. We present it here since

It allows us to introduce iterative/recursive definitions.
Its generality allows us to explain some variants of regular induction (e.g., why we can start at $n=4$ if we want to.)

Well Ordering Principle and Proof by Infinite Descent

The Well Ordering Principle

Let $S \subseteq\mathbb{N}$ be a non-empty subset, $a$ is a minimal element of $S$ if $\forall b \in S. (a\leq b)$

The Well Ordering Principle states that for any non-empty subset $S \subseteq\mathbb{N}$, $S$ has a minimal element.

In particular, this is true even for infinite subsets.

Thoughts? Is this obvious?

Well Ordering Principle

Well Ordering Principle: For any non-empty subset $S \subseteq\mathbb{N}$, $S$ has a minimal element.

What if we replace $\mathbb{N}$ with $\mathbb{Q}, \mathbb{Z}, \mathbb{R}$? Is it still true?

Solution

No!

Proofs using the Well Ordering Principle

The Well Ordering Principle also lets us prove statements of the form $\forall n \in \mathbb{N}. (P(n))$. Here’s how:

Check $P(0)$ is true.
By contradiction, assume $\exists n \in \mathbb{N}. (\neg P(n))$. So the set $S = \{n \in \mathbb{N}: \neg P(n)\}$ is non-empty.
By the Well Ordering Principle, $S$ has a minimal element, $m$ (i.e. $m$ is the smallest natural number for which $P$ doesn’t hold.) Since we know $P(0)$, $m \geq 1$.
Derive a contradiction by showing $P(m)$, or by finding a $m' < m$, for which $\neg P(m')$.

For all $n \in \mathbb{N}, n\geq 2.$ $n$ has a prime divisor

Solution

A prime divisor $p$ of a number $n$ is a prime number such that there exists $k \in \mathbb{N}$ such that $pk = n$.

By contradiction, assume $\exists k \in \mathbb{N}, k \geq 2$ that does have a prime divisor. Let

\[ S = \{k \in \mathbb{N}: k \geq 2, \text{and $k$ doesn't have a prime divisor}\} \]

By WOP, $S$ has a minimal element $m$. If $m$ is prime, then $m$ is a prime divisor of itself. Thus, $m$ is not prime. Hence $m = ab$ for $1 < a,b < m$. Since $a < m$, and $m$ was minimal in $S$, $a \notin S$, and hence $a$ has a prime divisor $c$. But since $m = ab$, $c$ is also a prime divisor of $m$, which contradicts the fact that $m \in S$.

$\sqrt 2$ is irrational (a classic)

Solution

Let $P(n)$ be the predicate, there does not exists $m \in \mathbb{N}, m \geq 1$ such that $n / m = \sqrt{2}$. If $\forall n. (P(n))$, then $\sqrt{2}$ can not be written as a fraction as is therefore irrational.

By contradiction, assume the set $S = \{n \in \mathbb{N}: \neg P(n)\}$ is non-empty. Then by the WOP, $S$ has a minimal element $x$. Since $x \in S$, there exists $y \in \mathbb{N}$ such that $x/y = \sqrt{2}$. Squaring both sides, we have $x^2 / y^2 = 2$. Thus, $x^2 = 2y^2$ and $x$ must be even. Therefore $x = 2z$ for some $z \in \mathbb{N}$. But then $(2z)^2 = 2y^2$, so $2z^2 = y^2$, so $y$ must also be even! Therefore, $(x/2)$ is an positive integer and $(y/2)$ is positive integer such that and with \[ \frac{(x/2)}{(y/2)} = \sqrt{2}. \]

Thus, $x/2 \in S$, which contradicts the minimality of $x$ in $S$.

Induction in disguise

Let’s take another look at the complete induction. We want to show that $P(0)$ and

\[ (\forall k \in \mathbb{N}. (P(0),...,P(k))) \implies P(k+1) \]

Usually, we prove the inductive step directly by picking an arbitrary $k \in \mathbb{N}$ and assuming $P(0)\land ...\land P(k)$, and then showing $P(k+1)$.

If we instead chose to do it by contradiction, it might look like this. Let $k \in \mathbb{N}$ be any natural number, and assume $P(0)\land ... \land P(k)$, by contradiction, assume $\neg P(k+1)$. At this point, our assumptions are

\[ P(0) \land ... \land P(k) \land \neg P(k+1). \]

Induction in disguise

But \[ P(0) \land ... \land P(k) \land \neg P(k+1) \]

is exactly what it means for $k+1$ to be the minimal element of the set $S = \{n \in \mathbb{N}: \neg P(n)\}$.

Thus, proving the inductive step for complete induction by contradiction amounts to finding a contradiction by assuming there was a minimal element of the set $S = \{n \in \mathbb{N}: \neg P(n)\}$, which is exactly the same as what we’d do in a proof using the WOP.

Additional notes

This presentation of structural induction loosely follows the one in A Mathematical Introduction to Logic by Herbert Enderton. So check that out as supplementary reading.
Our approach for proving a mathematical statement using the Well Ordering Principle is sometimes called ‘proof by infinite descent’. Read all about that here.

Lecture 04: Induction 2

While we wait…

Recap

Announcement: Tutorial today

Induction and Complete Induction

Intuition: why does (regular) induction work again?

Intuition: why does (complete) induction work again?

Postage Stamps

Rephrasing the problem mathematically

Proof, attempt 1 (wrong!)

Problem

Proof 1. multiple base cases

Proof 2. Regular induction

Structural Induction

Induction

Another view of \(\mathbb{N}\)

Defining Sets Inductively

Alternatively

Example: \(\mathbb{N}\)

Example: \(\mathbb{Z}\)

Example: \(\texttt{List}[X]\)

Propositional logic

Structural Induction

Structural Induction (Formally)

Recovering regular induction

Flexibility

Perfect Binary Trees (Again)

An alternate way of looking at things

Perfect Binary Trees

\(\mathrm{JoinPerfectTrees}\)

A perfect binary tree of height \(h\) has \(2^{h+1} - 1\) vertices

Postage Stamps (Again)

Structural vs. Complete Induction

Construction Sequences

Example - construction sequence

Structural vs. Complete Induction

Perfect Binary Trees (again again)

Level of Formality

Well Ordering Principle and Proof by Infinite Descent

The Well Ordering Principle

Well Ordering Principle

Proofs using the Well Ordering Principle

For all \(n \in \mathbb{N}, n\geq 2.\) \(n\) has a prime divisor

\(\sqrt 2\) is irrational (a classic)

Induction in disguise

Induction in disguise

Additional notes

A trusty toolkit