Lecture 03: Induction 1
2025-05-21
While we wait
- What’s the most interesting thing you’ve learned recently (outside of class)?
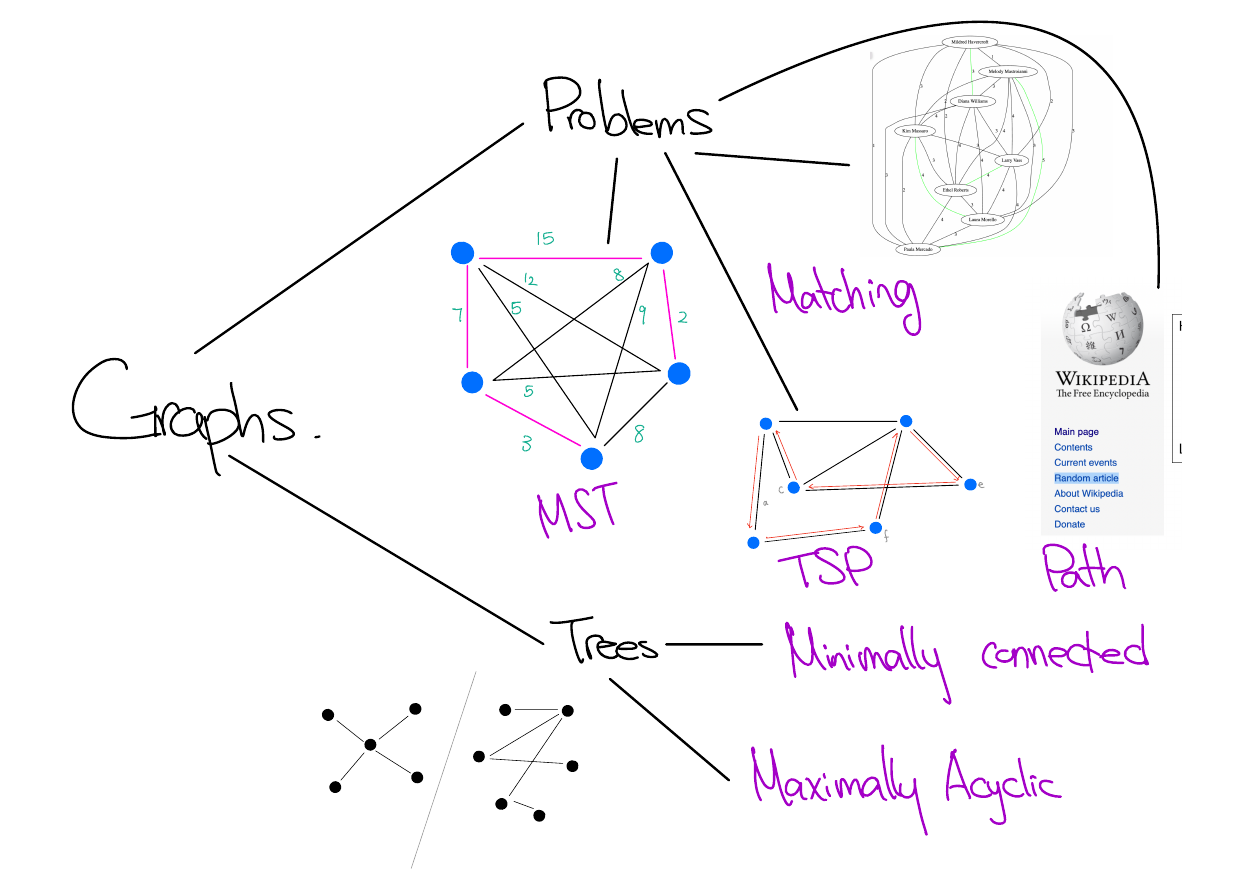
Recap: Graphs
Induction
What is induction used for
Induction is used to prove statements of the following form: \[\forall n \in \mathbb{N}. (P(n)).\]
Note that \(P\) is a predicate on the natural numbers. I.e., for any natural number \(n\), \(P(n)\) is either true or false. For example, \(P(n)\) might be
The sum of the first \(n\) odd numbers is \(n^2\).
\((12^n - 1)\) is divisible by 11.
Trees with \(n\) vertices have \(n-1\) edges.
Induction is super useful when analyzing the correctness and runtime of algorithms.
Induction

Induction
\[(P(0) \land \forall k \in \mathbb{N}.(P(k) \implies P(k+1))) \implies \forall n \in \mathbb{N}. (P(n))\]
Induction
\[(P(0) \land \forall k \in \mathbb{N}.(P(k) \implies P(k+1))) \implies \forall n \in \mathbb{N}. (P(n))\]
“If I can show that the first domino falls, and I can show that for any domino, if that domino falls, the next one falls, every domino falls”.
Here, the \(k\)th domino falling is analogous to \(P(k)\) being true.
Proofs by induction
\[(P(0) \land \forall k \in \mathbb{N}.(P(k) \implies P(k+1))) \implies \forall n \in \mathbb{N}. (P(n))\]
If we want to prove a statement of the form \(\forall n \in \mathbb{N}. (P(n))\), it suffices to prove
\(P(0)\) (base case)
\(\forall k \in \mathbb{N}.(P(k) \implies P(k+1))\) (inductive step)
Induction template
Suppose we want to prove \(\forall n \in \mathbb{N}. (P(n))\). Here is the template:
By induction.
Base case. [Prove \(P(0)\) is true]
Inductive step. Let \(k \in \mathbb{N}\) be an arbitrary natural number, and assume \(P(k)\). We’ll show \(P(k+1)\). [Prove \(P(k+1)\) assuming \(P(k)\)]. This completes the induction.
Flexibility
There is some flexibility in the proof by induction template. For example, sometimes, we want to prove a statement is true for all \(n \geq 1\), so the base case starts at 1 instead of 0. Sometimes, for the inductive step, we need to show that if the previous two dominoes fall, then the next one will also fall. In this case, we would need to prove two base cases. These will come up in the examples, and you will see why we can do this next week.
You should be okay as long as you showed enough so that “all the dominoes fall”.
Examples of Proofs by Induction
Binary Trees
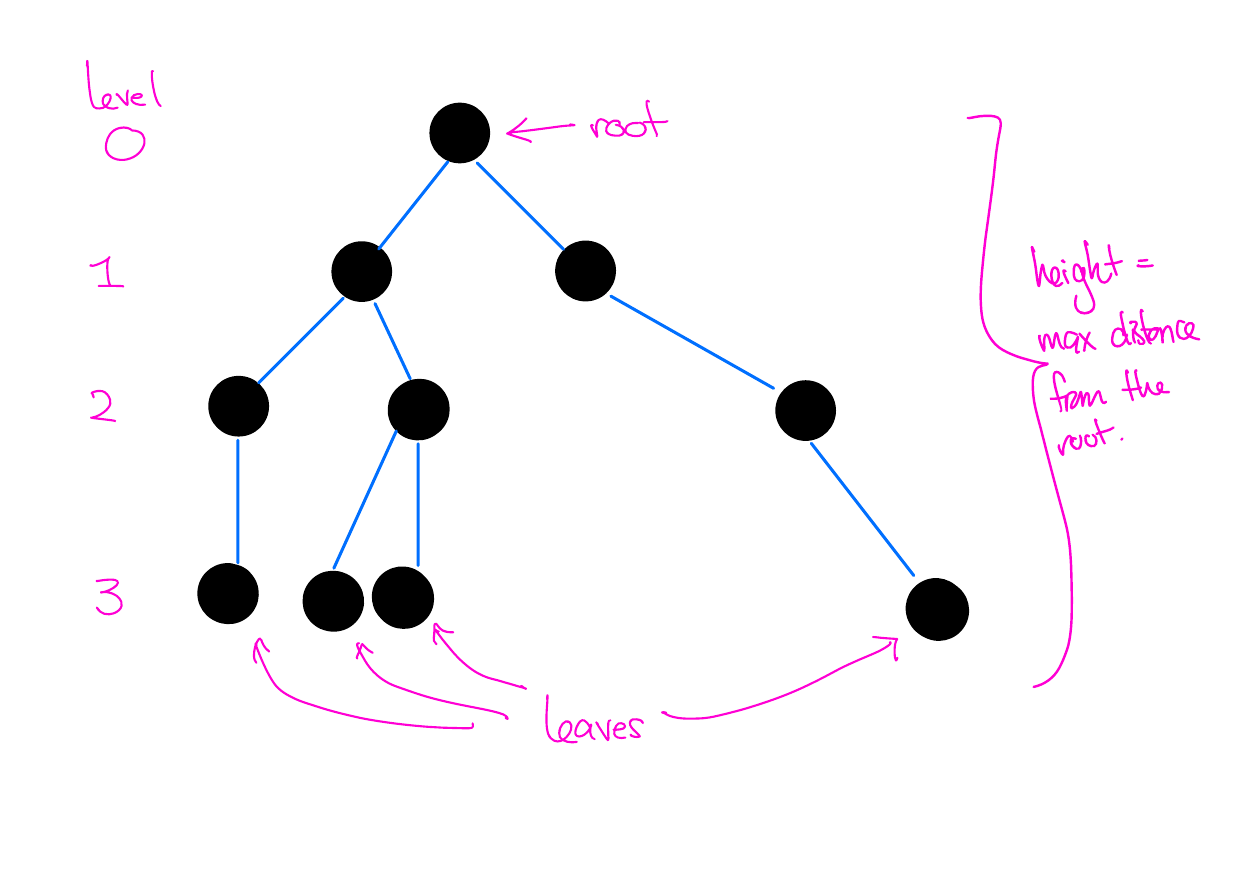
Perfect binary trees
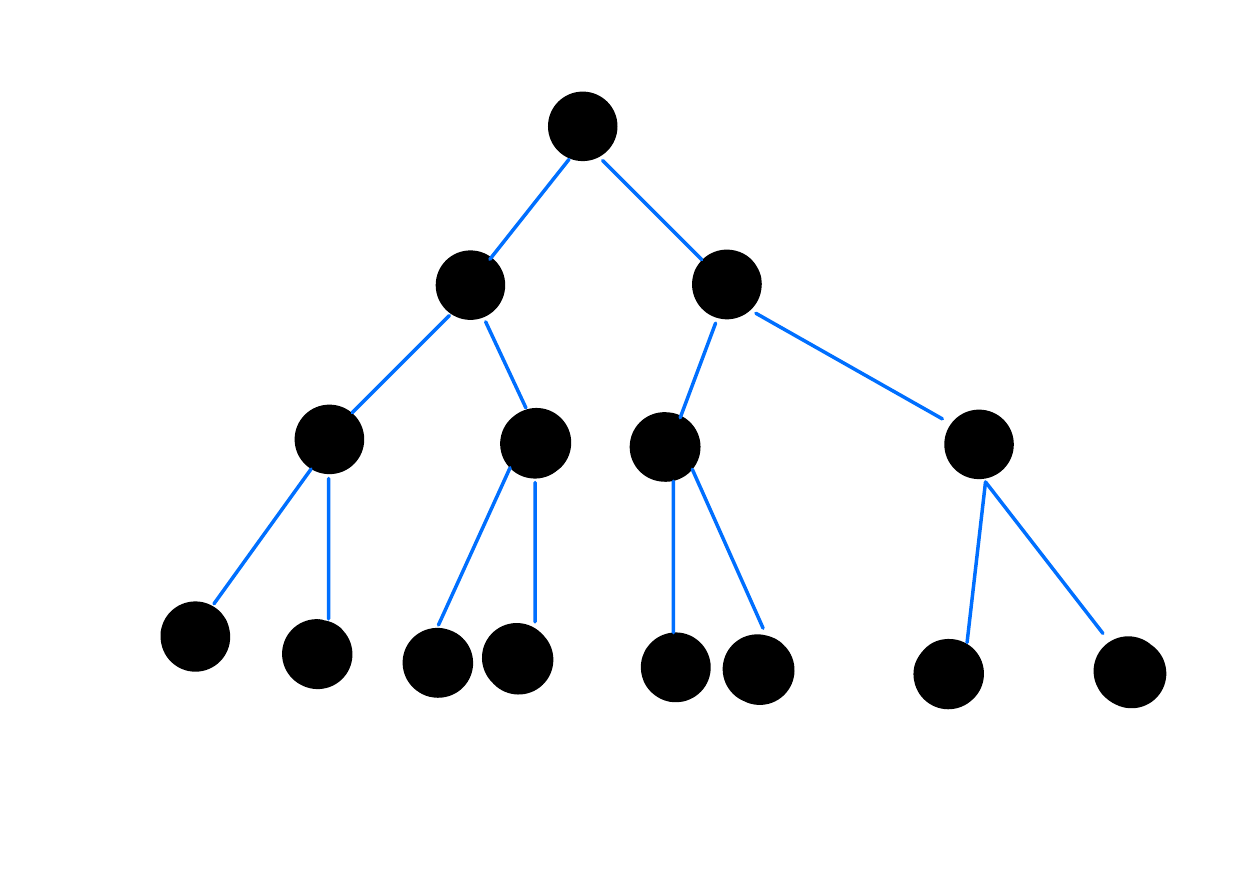
In a perfect binary tree, all leaves are at the same level, and every other vertex has two children and one parent (except for the root, which does not have a parent).
Number of vertices of perfect binary trees
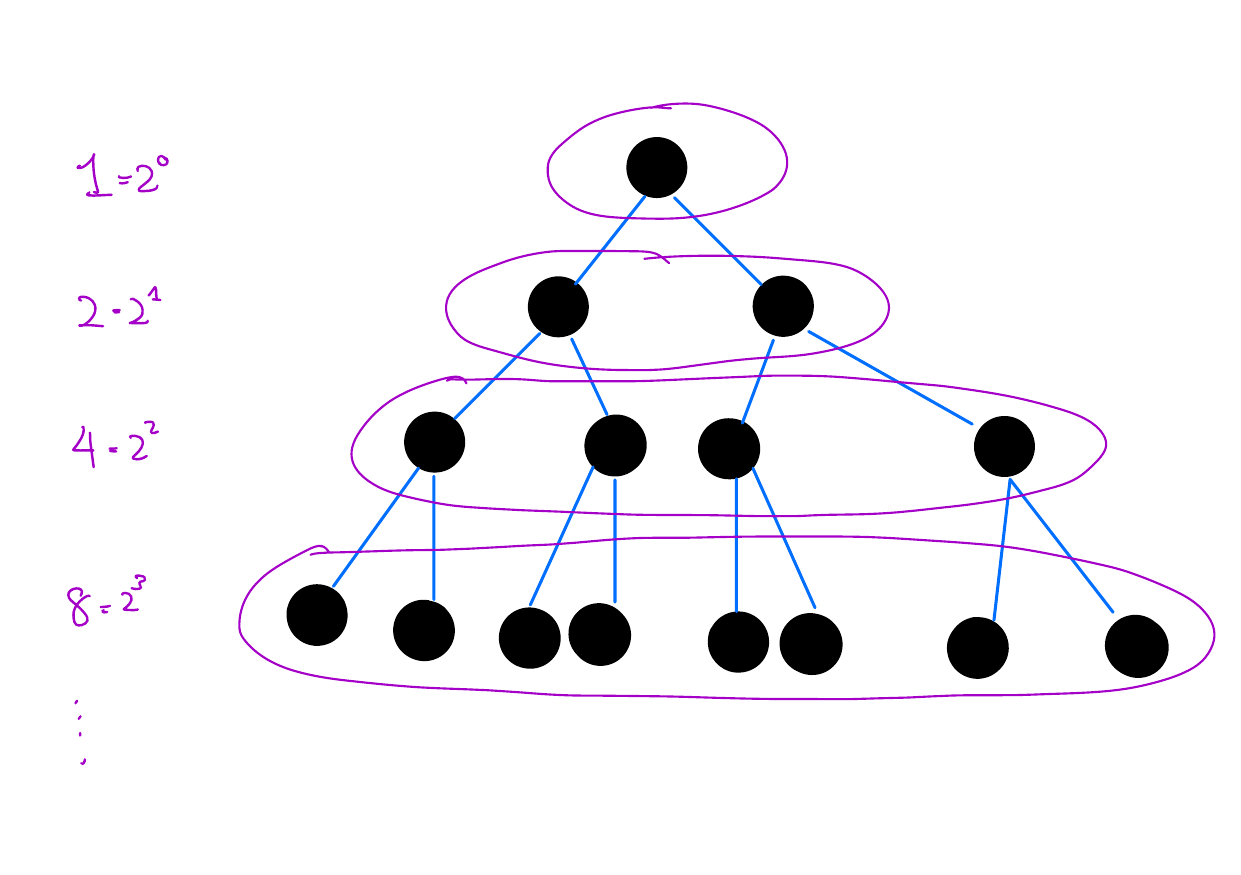
How many vertices does a perfect binary tree of height \(n\) have?
\(\forall n \in \mathbb{N}. (2^0 + 2^1 +...+2^n = 2^{n+1} - 1)\)
Solution
By induction.
Base case. For the base case, we need to check \(2^0 = 2^{0+1} -1\). This holds since they are both equal to 1.
Inductive step. Let \(k \in \mathbb{N}\) be an arbitrary natural number, and assume \(\sum_{i=0}^k2^i = 2^{k+1} - 1\). We’ll show \(\sum_{i=0}^{k + 1}2^i = 2^{k+2} - 1\). We have \[ \begin{align*} \sum_{i=0}^{k + 1}2^i & = 2^{k+1} + \sum_{i=0}^{k}2^i \\ & = 2^{k+1} + 2^{k+1} - 1 \\ & = 2^{k+2} - 1, \end{align*} \] as required.Another way to do it…
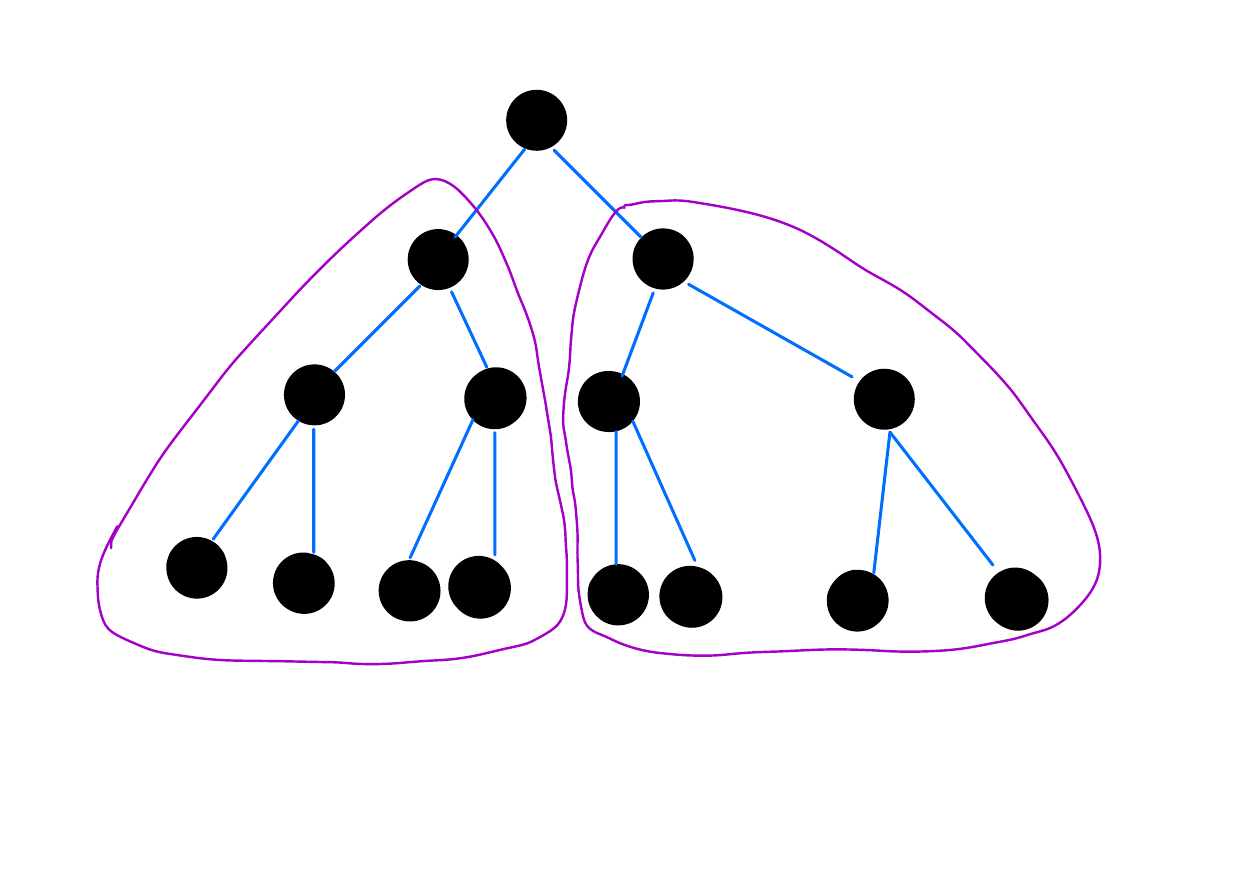
We’ll see next time.
Sum of first \(n\) odd numbers is the \(n\)th square
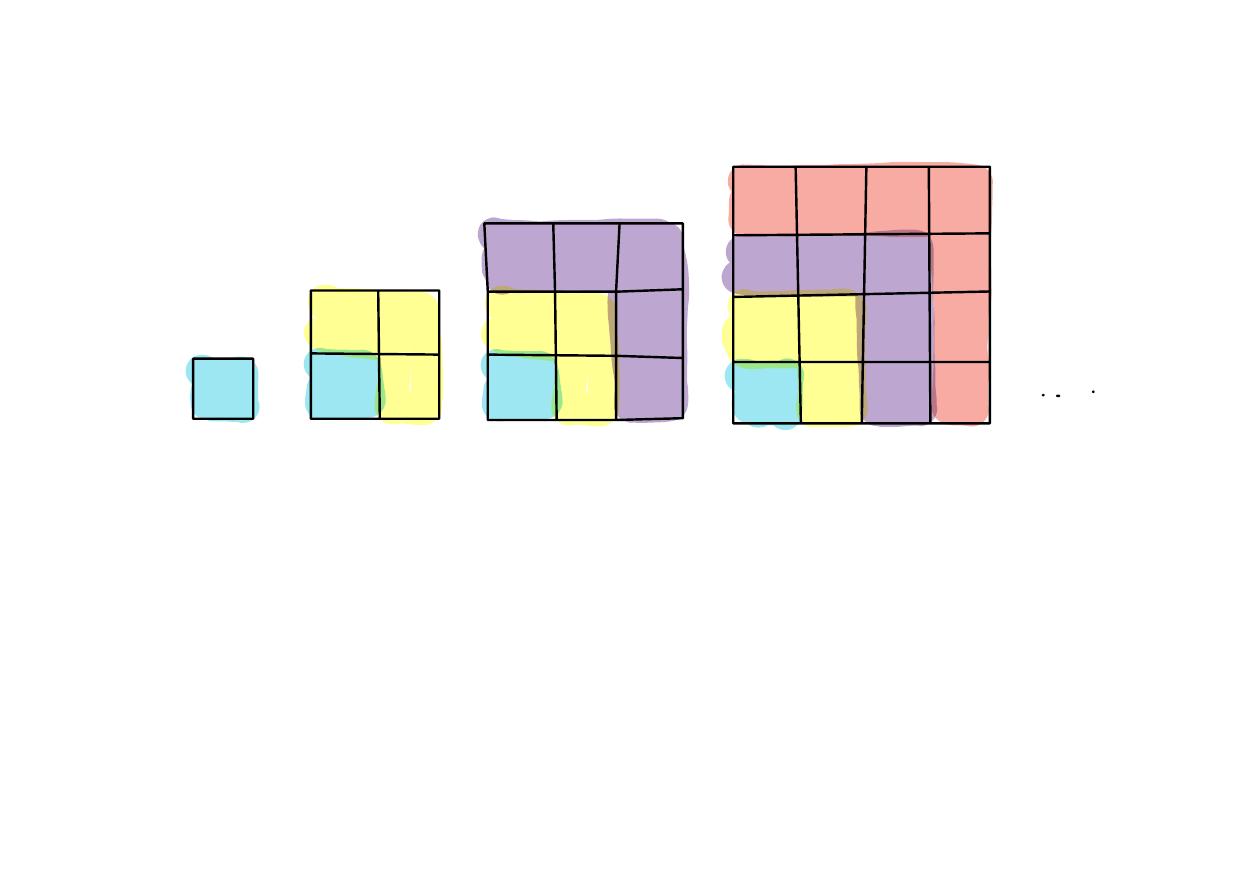
Sum of first \(n\) odd numbers is the \(n\)th square
Solution
We want to prove \(\forall n \in \mathbb{N}, n \geq 1. (\sum_{i=1}^n 2i-1 = n^2)\).
Base case. \(2\cdot 1 - 1 = 1 = 1^2,\) so the base case holds. Note that we prove \(P(1)\) instead of \(P(0)\) since the statement we are trying to prove starts at 1.
Inductive step. Let \(k \in \mathbb{N}, k \geq 1\) be an arbitrary natural number, and assume \(\sum_{i=1}^k 2i-1 = k^2\). We’ll show \(\sum_{i=1}^{k + 1}2i-1 = (k+1)^2\).
\[ \begin{align*} \sum_{i=1}^{k + 1}2i-1 & = 2(k+1) - 1 + \sum_{i=1}^{k}2i-1 \\ & = 2k+1 + k^2 \\ & = (k+1)^2 \end{align*} \]
as required.
Takeaways:
- To apply induction effectively, you need to formulate the statement you want to prove as \(\forall n \in \mathbb{N}. (P(n))\).
- In the inductive step, when trying to prove \(P(k+1)\), you’re always looking for any opportunity to use the inductive hypothesis \(P(k)\). This typically means you want to express \(P(k+1)\) in terms of \(P(k)\).
\(\forall n \in \mathbb{N}. (n^3 - n + 3)\) is divisible by \(3\)
Solution
By induction.
Base case. For the base case, we have \(0^3 - 0 + 3 = 3\) which is divisible by \(3\).
Inductive step. Let \(k \in \mathbb{N}\) by any natural number and assume \(k^3 - k + 3\) is divisible by \(3\), i.e. \(k^3 - k + 3 = 3p\) for some \(p \in \mathbb{N}\). We will show \((k+1)^3 - (k + 1) + 3\) is also divisible by \(3\). We have \[ \begin{align*} (k+1)^3 - (k + 1) + 3 & = k^3 + 3k^2 + 3k + 1 - k - 1 + 3 \\ & = (k^3 - k + 3) + 3k^2 + 3k + 1 - 1 \\ & = 3p + 3k^2 + 3k \\ & = 3(p + k^2 + k) \end{align*}, \]
as required.\(\forall n \in \mathbb{N}. \text{ the units digit of } 7^n\) is 1, 3, 7, or 9
Solution
By induction.
Base case. \(7^0 = 1\), so the base case holds.
Inductive step. Let \(k \in \mathbb{N}\) be an arbitrary natural number, and assume the units digit of \(7^k\) is either \(1, 3, 7\) or \(9\). There are several cases.
- If it was \(1\), \(7^{k+1}\) has units digit \(7\).
- If it was \(3\), \(7^{k+1}\) has units digit \(1\).
- If it was \(7\), \(7^{k+1}\) has units digit \(9\).
- If it was \(9\), \(7^{k+1}\) has units digit \(3\).
\(\forall n \in \mathbb{N}. \text{ the units digit of } 7^n\) is 1, 3, 7, 9 or 2
Note the only difference here is that we are adding \(2\) to the list of possible units digits.
Is this still true?
Solution
Yes! Since it’s a strictly weaker statement (it’s implied by the previous one since \(\{1, 3, 7, 9\} \subseteq \{1, 2, 3, 7, 9\}\))If we try to directly prove it by induction, however, we run into a problem.
Attempted proof by induction:
Base case. \(7^0 = 1\), so the base case holds.
Inductive step. Let \(k \in \mathbb{N}\) be an arbitrary natural number, and assume the units digit of \(7^k\) is either \(1, 2, 3, 7\) or \(9\). There are several cases.
- If it was \(1\), \(7^{k+1}\) has units digit \(7\).
- If it was \(2\), \(7^{k+1}\) has units digit \(4\)
- …
This is a problem since \(4\) is not in the set of possible units digits!
Takeaway: In this case, the inductive hypothesis is not strong enough to prove the inductive step. In particular, sometimes it can be harder to prove a weaker statement by induction since the inductive hypothesis will also be weaker!
\(\forall n \in \mathbb{N}. (n^2 \leq 2^n)\)
False! E.g., for \(n = 3\), the LHS is 9 and the RHS is 8.
\(\forall n \in \mathbb{N}, n \geq 4.(n^2 \leq 2^n)\)
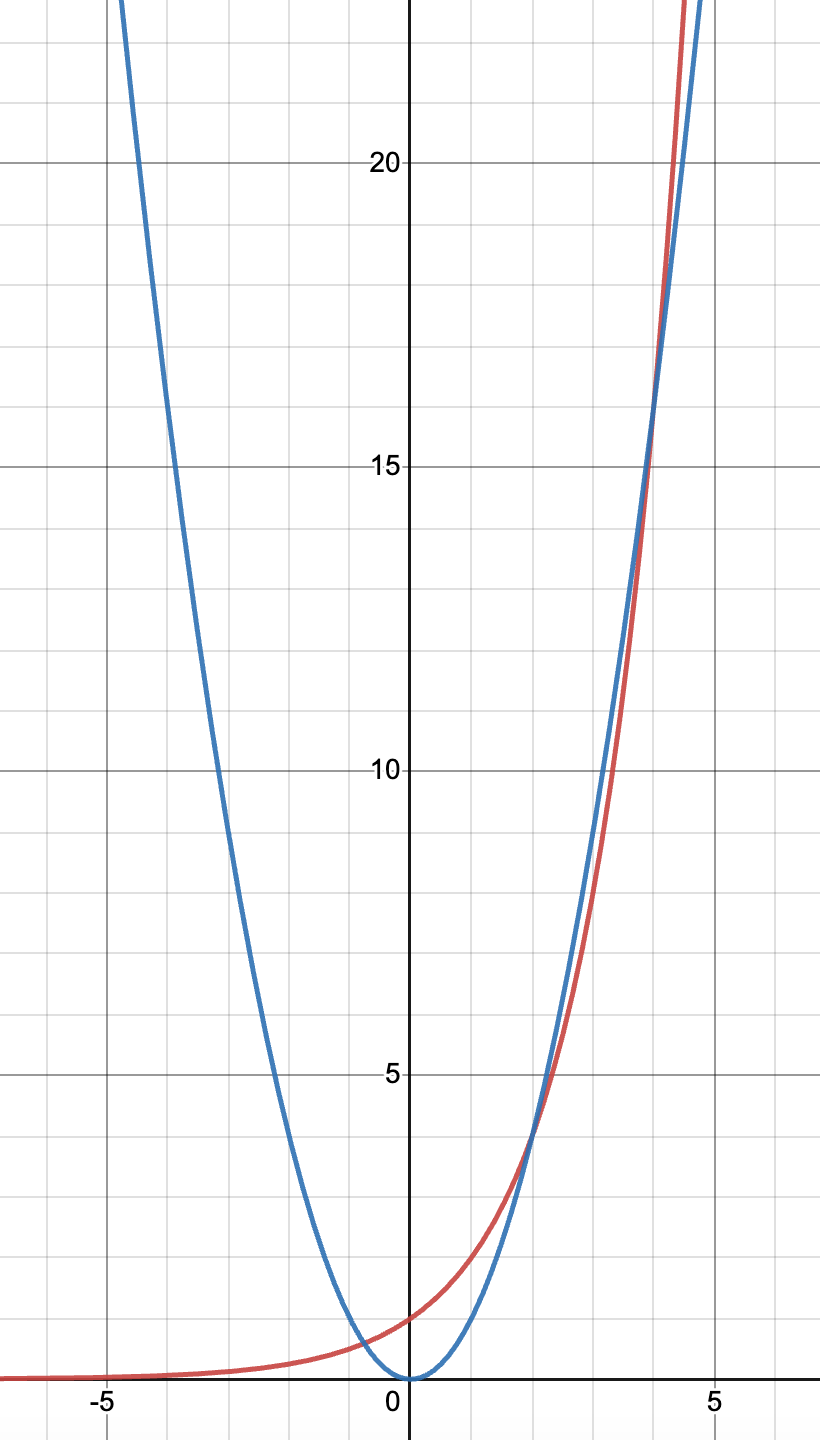
\(\forall n \in \mathbb{N}, n \geq 4.(n^2 \leq 2^n)\)
Solution
By induction.
\(4^2 = 16\) and \(2^4 = 16\), so the base case holds.
Let \(k \in \mathbb{N}\) be an arbitrary natural number with \(k \geq 4\), and assume \(k^2 \leq 2^{k}\). We’ll show \((k+1)^2 \leq 2^{k+1}\). We have
\[ \begin{align*} (k+1)^2 & = k^2 + 2k + 1 \\ & \leq k^2 + (k-2)k + 1 & (k-2 \geq 2) \\ & = k^2 + k^2 - 2k + 1 \\ & \leq 2k^2 & (-2k + 1 \leq 0) \\ & \leq 2\cdot 2^k & (\text{IH}) \\ & = 2^{k+1}, \end{align*} \]
completing the induction.
Takeaway: In the inductive step, we crucially used the fact that \(k \geq 4\). Here, since we only cared about \(n \geq 4\), we can alter the inductive step to show \(\forall k \in \mathbb{N}, k \geq 4. P(k) \implies P(k+1)\). I.e. we don’t care if \(P(1) \implies P(2)\). In particular, this allows us to assume \(k \geq 4\) in the inductive step.
All birds have the same color1
Claim. \(\forall n \in \mathbb{N}\), a set of \(n\) birds will all have the same color.
Is this claim true?
Solution
No, of course not!
All birds have the same color - “proof”
Claim. \(\forall n \in \mathbb{N}\), a set of \(n\) birds will all have the same color.
Base Case. For \(n = 0\), the claim is vacuously true.
Inductive step. Let \(k \in \mathbb{N}\) be any number and assume a set of \(k\) birds will all have the same color. Let \(S\) be a set of \(k + 1\) birds. We’ll show that all the birds in \(S\) have the same color.
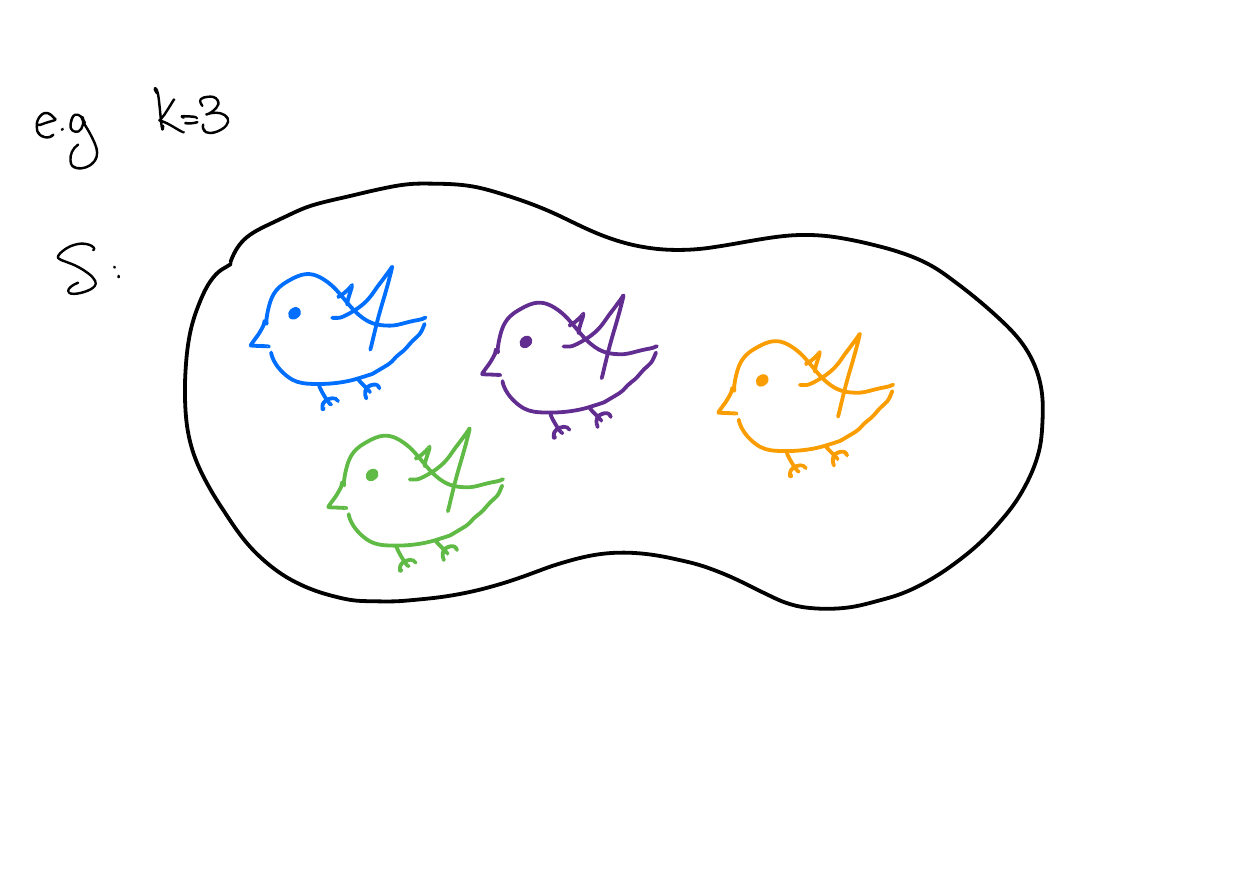
Remove an arbitrary bird \(b_1\). 
The remaining \(k\) birds must have the same colour by the inductive hypothesis. 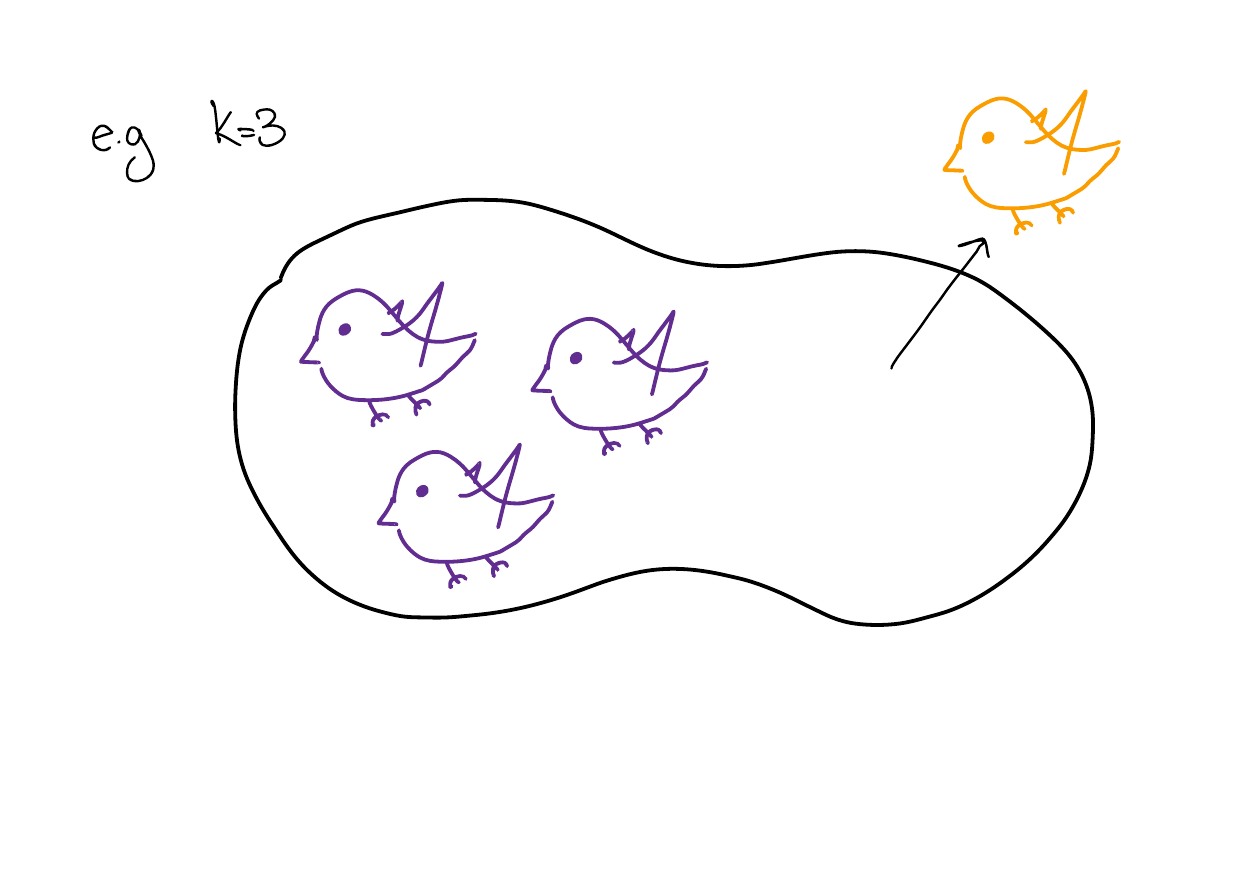
Add back the removed bird and now remove a different bird \(b_2\). 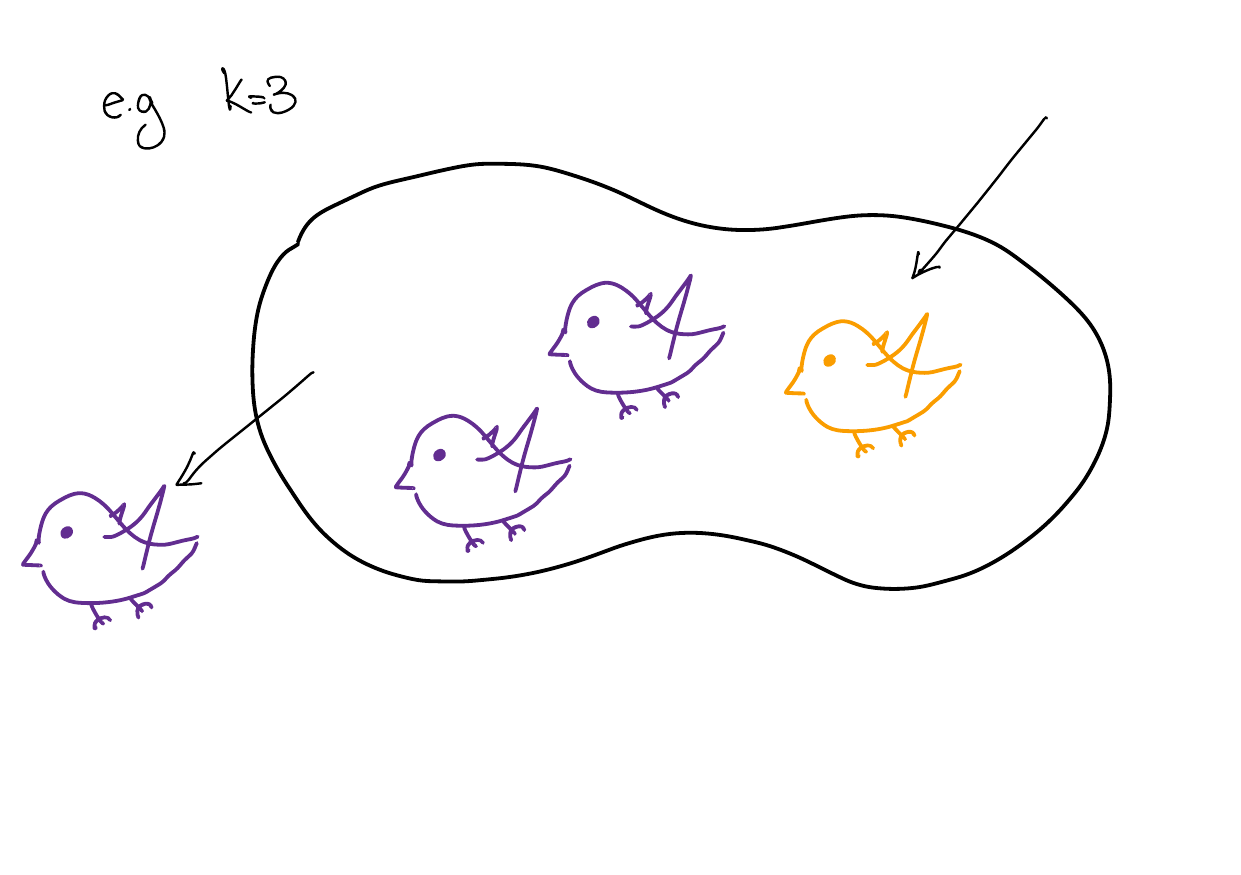
By the same reasoning, the remaining \(k\) birds must have the same color. Therefore, \(b_1\) has the same colour as birds which have not been removed, which in turn have the same colour as \(b_2\).
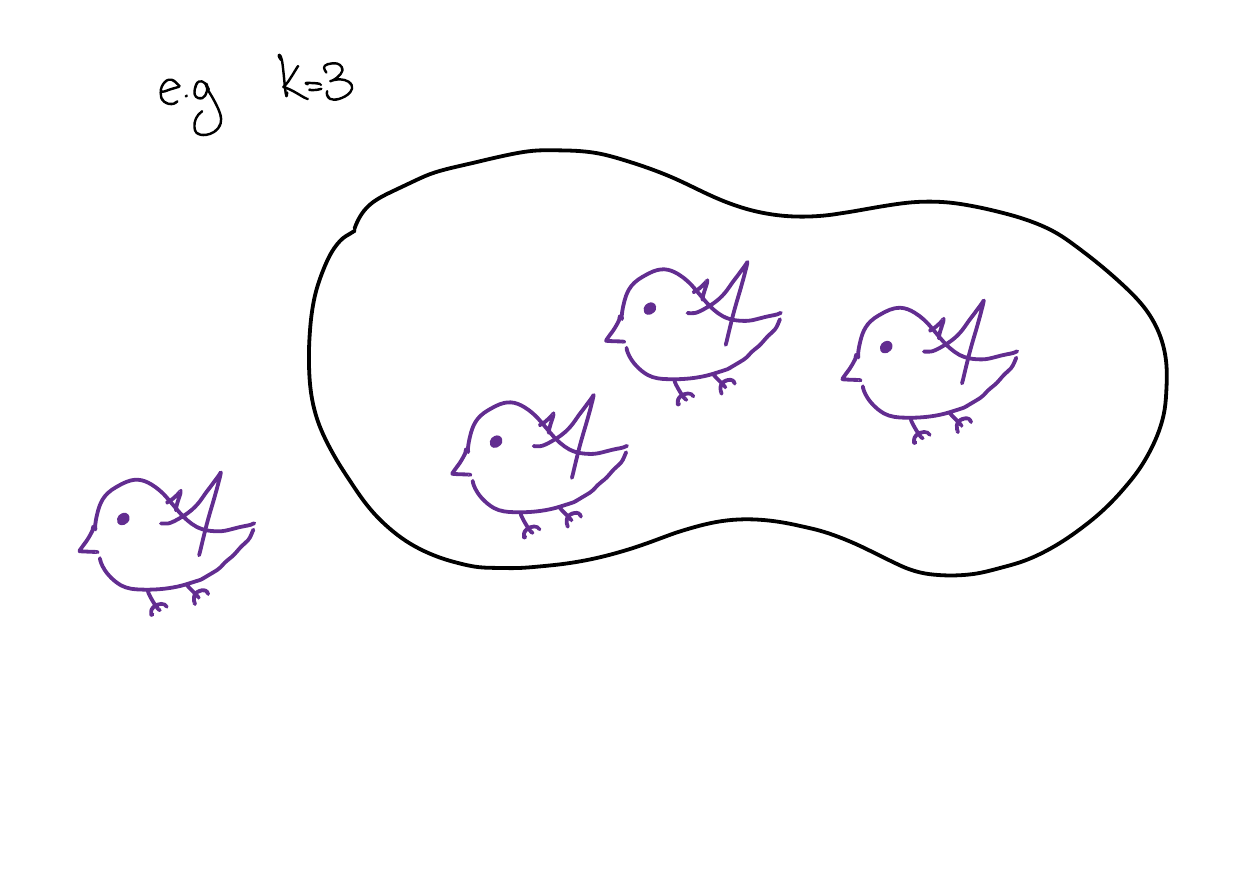
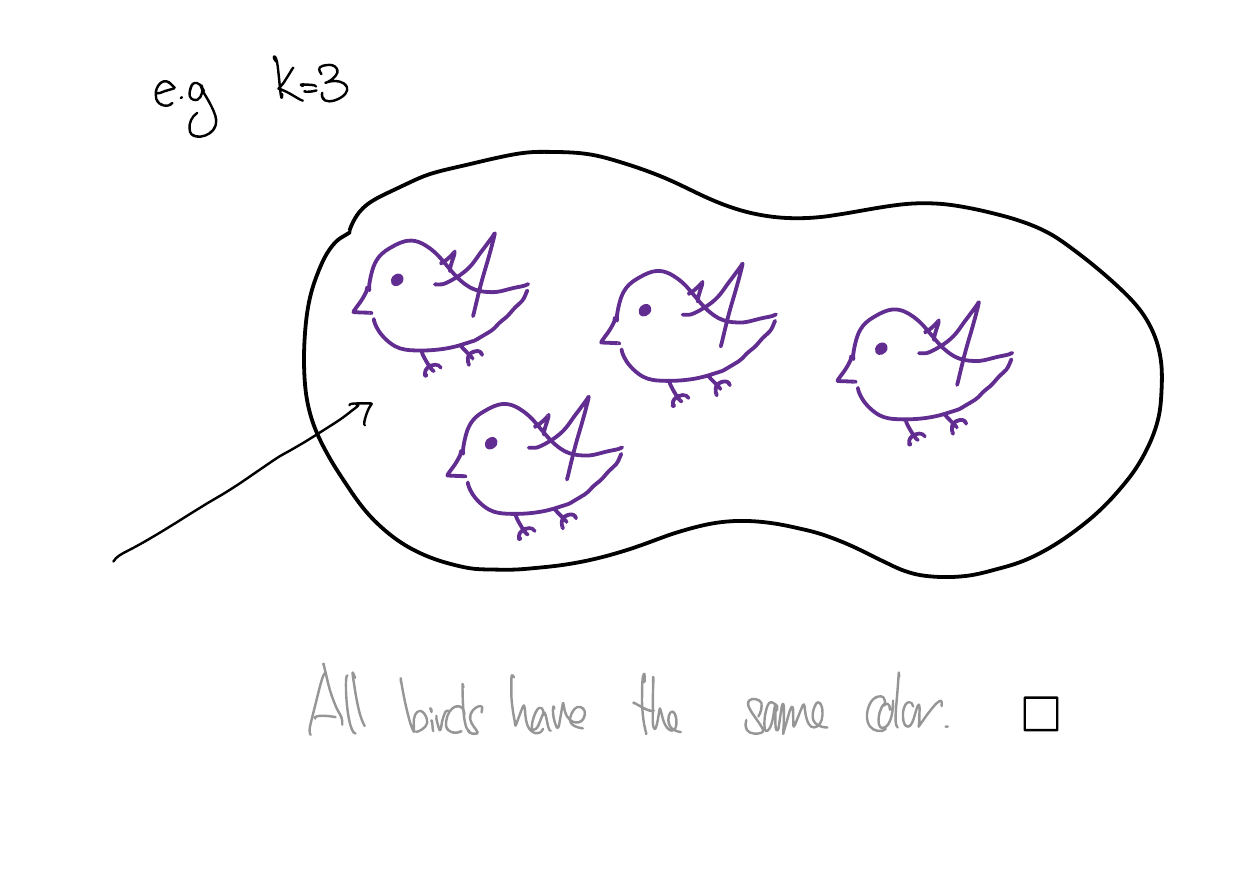
What went wrong?
Solution
There is an implicit assumption here that there is another bird other than \(b_1\) and \(b_2\)! I.e., for this to hold, we need \(|S|\geq 3\)! In particular, it does not hold for \(k = 1\) (\(|S| = 2\)).Takeaway: Induction can be tricky! Make sure your inductive step does not assume anything more than what you claim! For example, in the \(n^2 \leq 2^n\) example, we could assume \(k \geq 4\) since we were restricting to the case where \(k \geq 4\), but we couldn’t do the same for the “all birds have the same color” example.
Complete Induction
Complete Induction
Complete induction is another way to prove statements of the form \(\forall n \in \mathbb{N}. (P(n))\).
Another way to get all the dominoes to fall
If I want to show \(\forall n \in \mathbb{N}. (P(n))\), it suffices to prove
\(P(0)\)
\(\forall k \in \mathbb{N}. ((P(0)\land P(1) \land ...\land P(k)) \implies P(k+1))\)
“If I can show that the first domino falls, and I can show that for any domino, if that domino falls and all previous dominoes fall, that the next one also falls, every domino falls”.
Complete Induction template
Suppose we want to prove \(\forall n \in \mathbb{N}. (P(n))\). Here is the template:
By complete induction.
Base case. [Prove \(P(0)\) is true]
Inductive step. Let \(k \in \mathbb{N}\) be an arbitrary natural number, and assume for every \(i \in \mathbb{N}\) with \(i \leq k\), \(P(i)\) holds. We’ll show \(P(k+1)\). [Prove \(P(k+1)\) using this assumption]
Chocolate
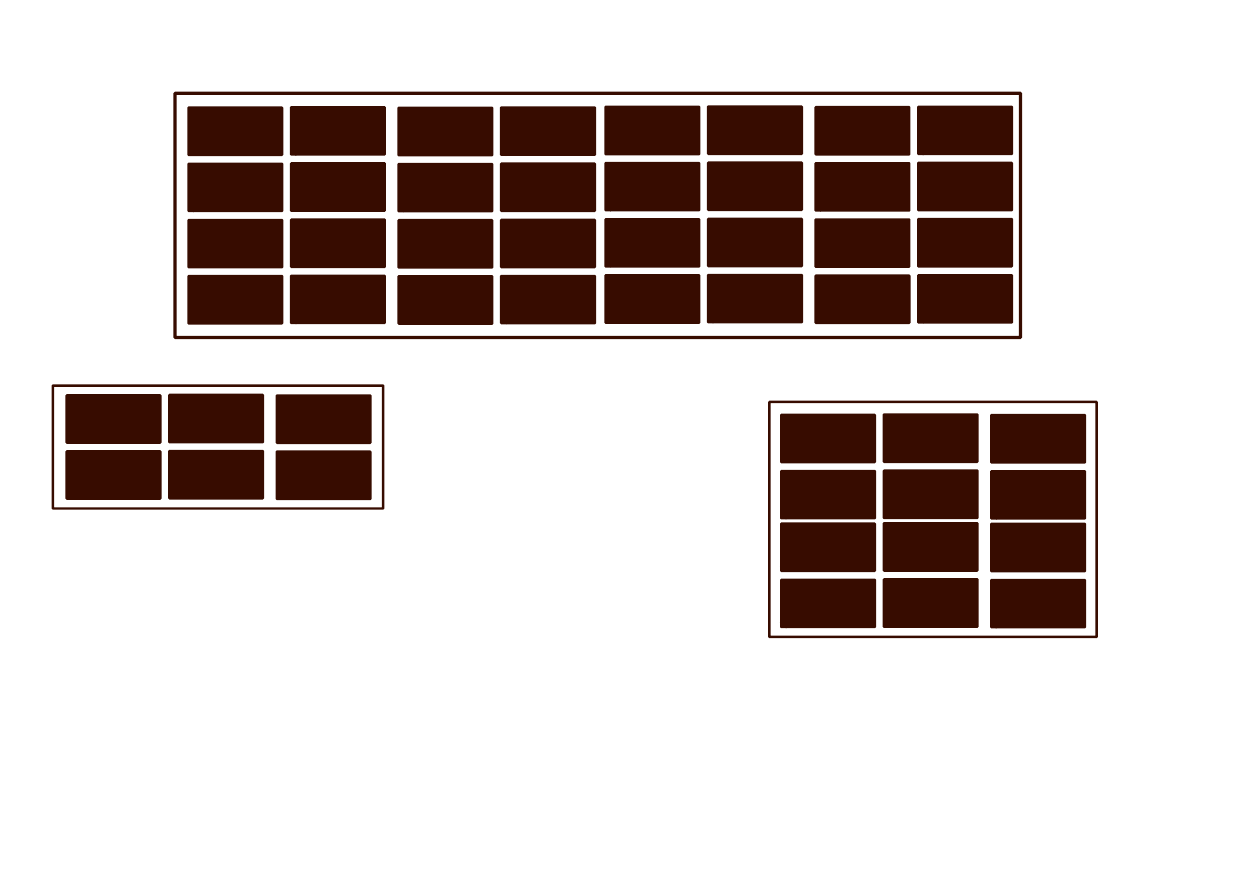
Chocolate - Attempted proof by regular induction
Claim: Let \(n \in \mathbb{N}, n \geq 1\) be any natural number. A chocolate bar with \(n\) individual pieces requires \(n-1\) breaks to split the bar into individual pieces.
Let \(P(n)\) be the predicate: A bar of chocolate composed of \(n\) individual pieces requires \(n-1\) breaks.
Base case. For \(n=1\), the chocolate bar is already a single piece of chocolate and thus requires \(1 - 1 = 0\) breaks.
Inductive step. Let \(k \in \mathbb{N}, k \geq 1\) be an arbitrary natural number at least 1, and assume \(P(k)\) is true. We need to show \(P(k+1)\) is true. Let \(B\) be a bar of chocolate with \(k+1\) pieces, and pick a way to break the chocolate. We are left with two blocks of chocolate, of sizes \(a\) and \(b\), respectively, where \(a + b = k + 1\).
Chocolate - Proof by Complete Induction
Solution
Let \(P(n)\) be the predicate: A bar of chocolate composed of \(n\) individual pieces requires \(n-1\) breaks.
Base case. For \(n=1\), the chocolate bar is already a single piece of chocolate and thus requires \(1 - 1 = 0\) breaks.
Inductive step. Let \(k \in \mathbb{N}, k \geq 1\) be an arbitrary natural number at least 1, and assume \(P(i)\) is true for all \(i \leq k\). We need to show \(P(k+1)\) is true. Let \(B\) be a bar of chocolate with \(k+1\) pieces, and select any way to break the bar. We are left with two blocks of chocolate of size \(a\) and \(b\) respectively, where \(a + b = k + 1\), \(a \leq k\), and \(b \leq k\). Applying the inductive hypothesis to each of these blocks, we have that the two blocks require \(a-1\) and \(b-1\) breaks respectively, so the total number of breaks (including the initial) is \(a + b - 2 + 1 = k\), as required.
Here’s the picture:
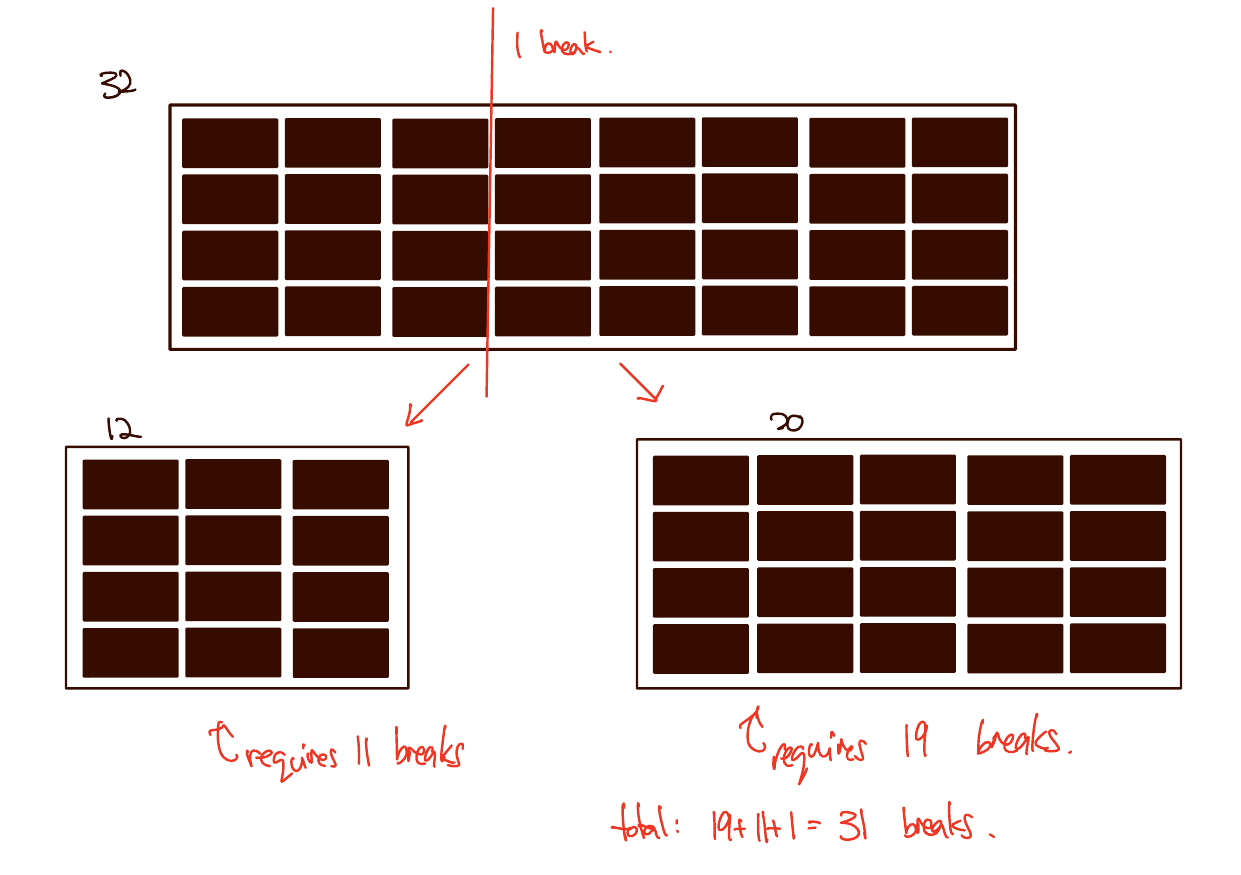
Takeaway: Complete induction gives you access to \(P(i)\) for all \(i \leq k\) in the inductive step. This was crucial since we don’t know what size the two blocks of chocolate are!
Number of Edges in a Tree
As a reminder, a tree is a graph \(G = (V, E)\) that is both acyclic (has no cycles) and connected (every pair of vertices is connected by some path). What was our conjecture from last time?
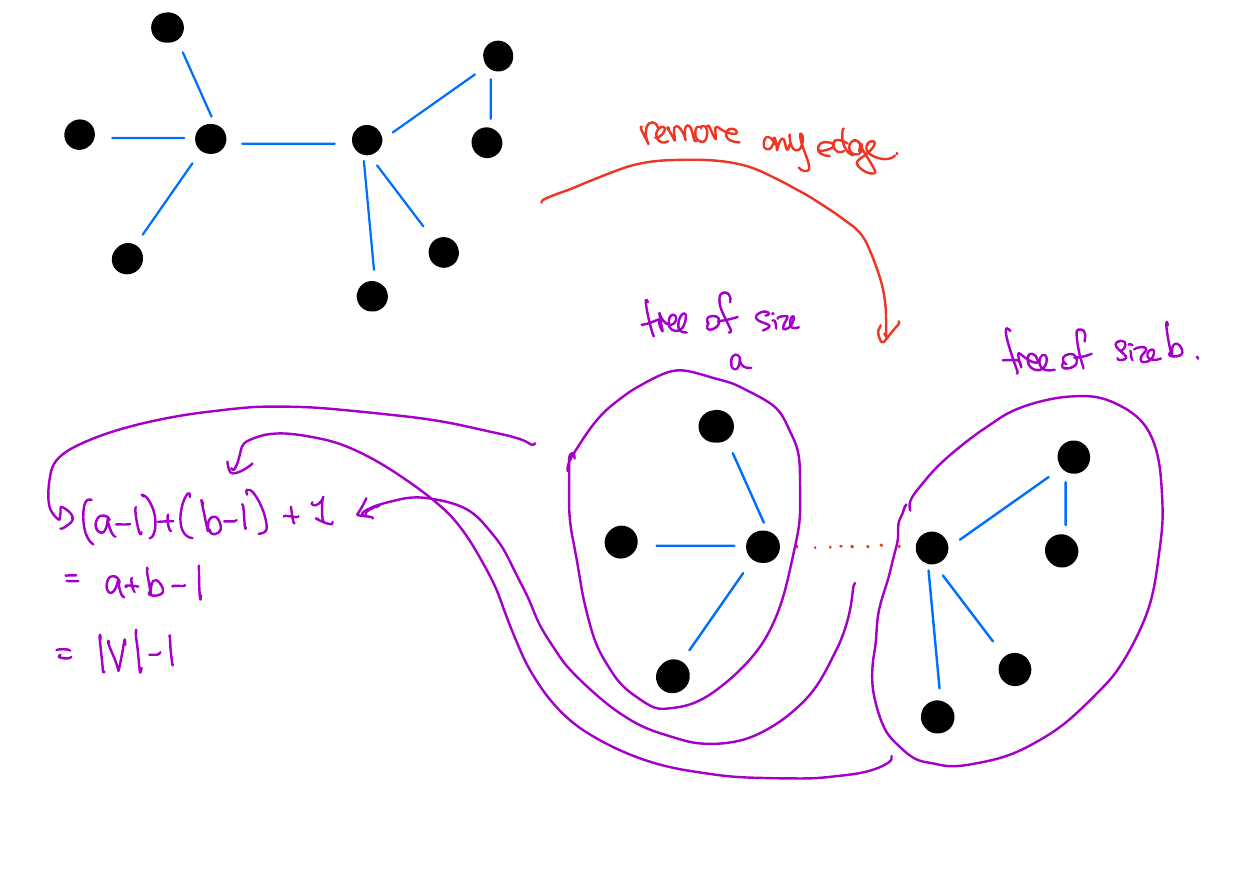
Solution
A tree with \(|V|\) vertices has \(|V| - 1\) edges.A tree has \(|V|\) - 1 edges
Why would I ever use regular induction if I can use complete induction?
You can always use complete induction if you wish! The inductive hypothesis is stronger (I.e., you get to assume \(P(0)\land...\land P(k)\) instead of just \(P(k)\)), but still lets you prove the same statement: \(\forall n \in \mathbb{N}. (P(n))\).
That being said, some mistakes are easier to make when using complete induction, and sometimes regular induction is easier to work with.
Induction and Algorithms
Proof by induction is an incredibly powerful technique that will allow us to prove strong guarantees about the runtime and correctness of algorithms.
I.e., Induction lets us prove \(\forall n \in \mathbb{N}. (P(n))\) consider what this means when
\(P(n)\) is: Algorithm X is correct on inputs of size \(n\).
\(P(n)\) is: Algorithm X is correct if the
forloop runs for at most \(n\) iterations.\(P(n)\) is: The runtime of Algorithm X is \(\Theta(n^2)\).
..etc.
A note about style
Sometimes you might find it easier to define a predicate in the following way: “Let \(P(n)\) be the predicate...” for example, in the chocolate example. This approach allows you to refer to the predicate easily. For example, defining \(P\) allows you to say “Assume \(P(k)\) is true...”
Other times, you might find it easier to directly work with the predicate without giving it a name, for example, in the divisibility example. This approach makes stating the inductive hypothesis more troublesome, but it reminds the reader of exactly what you’re trying to prove.
Both are fine!
Additional Notes
Induction and recursive algorithms are closely linked. Think of how! We will explore this in future classes.
Induction is a challenging concept to grasp. In particular, it takes a little bit of faith to believe that simply showing a base case and an inductive step allows us to prove a statement is true for all natural numbers. It’s good to keep the domino analogy in mind, i.e., when writing your proofs, ask - ‘did I show all the dominoes fall?’
Although intuition is important, at the end of the day, remember that the base case and inductive step are both mathematical statements that you need to prove. I.e., you should approach proving \(\forall k \in \mathbb{N}. (P(k) \implies P(k+1))\) like you would approach proving any other FOL statement.
CSC236 Summer 2025