Lecture 12: Review, Preview, and Goodbye
2025-08-06
Last time
Regular Languages
To show a language is regular, we can
- Find a DFA
- Find a NFA
- Find a regular expression
- Decompose it into simpler langauge and use closure properties (as you saw in tutorial).
- If the language is finite, then it’s automatically regular (as you saw in your homework).
Non-Regular Languages
To show a language is not regular, use the Myhill-Nerode Theorem.
Find a set of strings \(S \subseteq \Sigma^*\) such that
- \(S\) is infinite.
- For every \(x, y \in S\), such that \(x \neq y\), there exists a string \(z\) such that \(xz \in L\) and \(yz \notin L\) (or vice versa).
Intuition
A language is regular if it can be computed using fixed, finite memory.
Exam Tips
Question Types
Similar to stuff you have seen in homework, lecture and tutorial.
The exam is cumulative, with a slight emphasis on Formal Language Theory.
The exam is not easy. It’s designed to be challenging in order to give you a chance to demonstrate your understanding of the material. I look over the exams before submitting the final grades, so if I see that people seem to have a better understanding of the course material than their grade reflects, I may make adjustments.
Here are the main question types that we have seen in the course and my recommendations for how to approach them in an exam and how to study for them.
Proofs about Functions
Write out the formal first order logic definitions for what you’re trying to prove. Let that guide your solution.
Study tips
Remember the intuition for injective/surjective/bijective. This might help you come up with a solution.
Remember the formal definitions for injective/surjective/bijective. This will help you write the proof.
Modeling with Graphs
Writing it up
Explicitly define your graph \(G = (V, E)\).
Tell me exactly what the vertex set \(V\) is.
Tell me exactly what the edge set \(E\) is.
State the corresponding graph problem.
Explain why a solution to the graph problem is a solution to the problem in question and vice versa.
Study tips
- Review the graph problem we have studied, and all the practice problems.
Proofs by induction
Recognizing when to do something by induction.
When the problem is something like \(\forall n \in \mathbb{N}. P(n)\).
When I give you an inductively/recursively defined set - that’s almost always structural induction.
Writing it up
When proving a statement, translate it into \(\forall n \in \mathbb{N}. P(n)\) (or for structural induction \(\forall x \in X. P(x)\), were \(X\) is an inductively defined set. This step will clarify your proof process.
Clearly label the base case and inductive step.
For the inductive step:
Clearly state your inductive hypothesis.
State what you’re trying to prove, i.e. \(P(k+1)\).
Clearly state where you are applying the inductive hypothesis.
Study tips
- Lots of practice.
Solving Recurrences
Deciding on a method
Can it be done using the Master Method? If so, use it!
Otherwise, draw the recursion tree to form a guess, and then use the substitution method.
Master Theorem
State clearly that the master theorem applies in this case. “This is a standard form recurrence with parameters \(a = ...\), \(b = ...\), \(f(n) = ...\)”
Calculate the leaf work, \(n^{\log_b(a)}\), and determine the case split.
Find an explicit \(\epsilon\) like 0.0000001 in the leaf/root heavy case.
In the root heavy case don’t forget the regularity condition!
Study tips
- Come up with some of your own recurrences and solve them (or test each other).
Substitution Method
Draw recursion tree for guess.
Write out your guess \(f(n)\).
Write out the recurrence \(T(n) = T(...) + ...\)
Substitute all the \(T(...)\)s on the RHS with \(c\cdot f(...)\)s, and replace the \(=\) with \(\leq\) for Big O or \(\geq\) for Big \(\Omega\)
You want the RHS to then be \(\leq cf(n)\).
Rearrange to find an appropriate value of \(c\).
Recursive Algorithm Correctness
Correctness is precondition implies postcondition.
Do complete induction on the size of the input.
The IH is that precondition implies postcondition for smaller instances.
To apply the IH, you need to prove the precondition holds for the recursive step, AND that the recursive step is indeed a smaller instance (and thus captured in the IH)
Iterative Algorithm Correctness
Do NOT try to do induction on the size of the input.
Define a loop invariant.
Trace the algorithm on some example inputs to get an idea of what each variable corresponds to.
Use that intuition to come up with a loop invariant.
It’s almost always useful to include: after the \(k\)th iteration \(i_k = ...\) where \(i\) is the iteration variable.
Sketch initialization, maintenance, and termination BEFORE writing it up. If everything seems to work out ok, you can start writing it up. Otherwise, you found something that didn’t work, so you need to update your LI.
Explicitly state your loop invariant: “\(P(n):\) After the \(n\)th iteration ...”
Prove initialization/maintenance/termination
Termination: Either use the loop invariant or the descending sequence strategy, and prove that the LI after the last iteration implies the postcondition.
Determining if a Language is Regular
- Intuition: regular \(\iff\) can be computed using fixed, finite memory.
Showing a langauge is regular
| Pros | Cons | |
|---|---|---|
| Regex | Fast, great for matching substrings/beginnings/endings | Easy to match too many things |
| NFA | Powerful, great for counting # of occurrences mod N | Slower than regex and can harder to check than DFAs |
| DFA | Safe. Once you write a DFA it is easier to check (don’t need to follow different sequence of choices) | Takes longer to write. |
Study tips
For all the language I have given you in lectures, tutorials, and homeworks, come up with DFAs/NFAs and regular expressions for them.
Get a lot of practice. This is particularly important for these kinds of problems since it increases the likelihood of you being able to relate a language on the exam to something you’ve seen before.
Closure
Questions of the form, suppose \(A\), \(B\) are regular, then so is (some transformation of \(A, B\))
Assume you have DFAs for \(A\), and \(B\).
Define a NFA based on the DFAs for \(A\) and \(B\).
Showing a langauge is not regular
To show \(A\) is not regular,
- Find \(S \subseteq\Sigma^*\) such that \(S\) is infinite and pairwise distinguishable relative to \(A\). Remember to cite that this is enough b/c of the Myhill-Nerode Theorem.
What is this graph from earlier?

Solution
\(G_{236} = (V, E)\)
\(V\) is the set of things we studied.
\(\{u, v\} \in E\) if and only if \(u\) and \(v\) are “directly related".
That was a LOT of stuff - congratulations
More in theory - a look ahead
Error Correcting Codes
A noisy channel
Error Correcting Codes
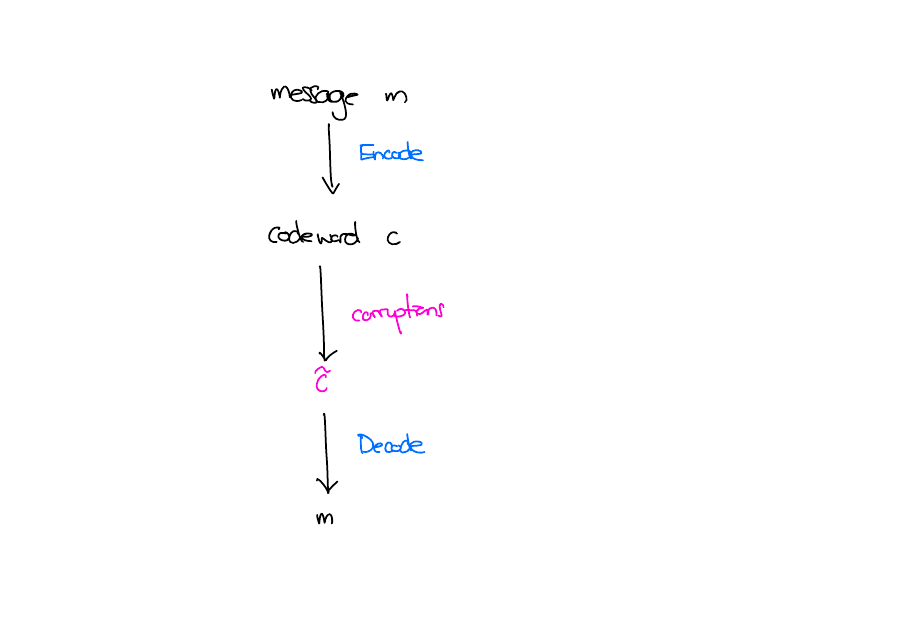
What do we want from error correcting codes?
We want to be able to decode from many errors.
There should be minimal overhead. I.e. \(c\) shouldn’t be much longer than \(m\) itself.
\(\mathrm{Enc}, \mathrm{Dec}\) should be fast.
Other applications
QR Codes
Hard drives
An Example
\[ \begin{align*} m &= \texttt{hello} \\ c = \mathrm{Enc}(m) &= \texttt{hellohellohello} \\ \tilde{c} &= \texttt{jellohillahelgo} \end{align*} \]
How do you correct the errors?
When will this strategy work/fail?Solution
It works for any single corruption. If there are two corruptions that occur at the same index in multiple copies (e.g. two of the three \(h\)s are corrupted to \(a\)), the decoded message will be wrong!How many errors can I guarantee to work on if I sent \(5\) copies instead of just \(3\)? How about \(2a+1\) in general for \(a \in \mathbb{N}\)?
Solution
Performance summary
Size blow up: \(3\) (\(2a+1\))
Errors decodable from: \(1\) (\(a\))
A size blow up of \(3\) to correct just a single error doesn’t seem that worth it! Can we do better?
A Slightly Better Example
\[ m \in \{0,1\}^4 \]
\[ c = m_1m_2m_3m_4(m_2\oplus m_3 \oplus m_4)(m_1 \oplus m_3 \oplus m_4)(m_1 \oplus m_2 \oplus m_4) \]
E.g. \(m = 1001\)
\(c = 1001100\)
Claim: We can correct from one error!
What is the message if this was the received codeword (with one error)
\[ \tilde{c} = 1110011 \]
Performance summary
Size blow up: \(7/4\)
Errors decodable from: \(1\)
We get the same error correction performance, but the blow up in the size of the message is only \(7/4\) instead of \(3\)!
A Mathematical Model
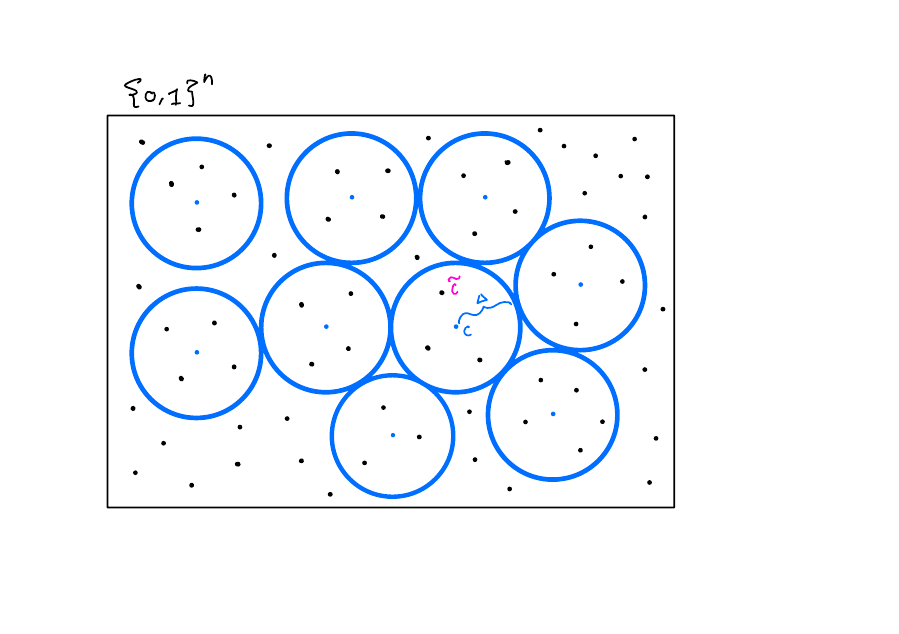
Interesting Facts and Questions
What is the optimal tradeoff between the size blow up and the number of errors you can correct from?
How can we construct codes that get a good tradeoff that also have good encoding and decoding algorithms?
Cryptography
Secure Messaging
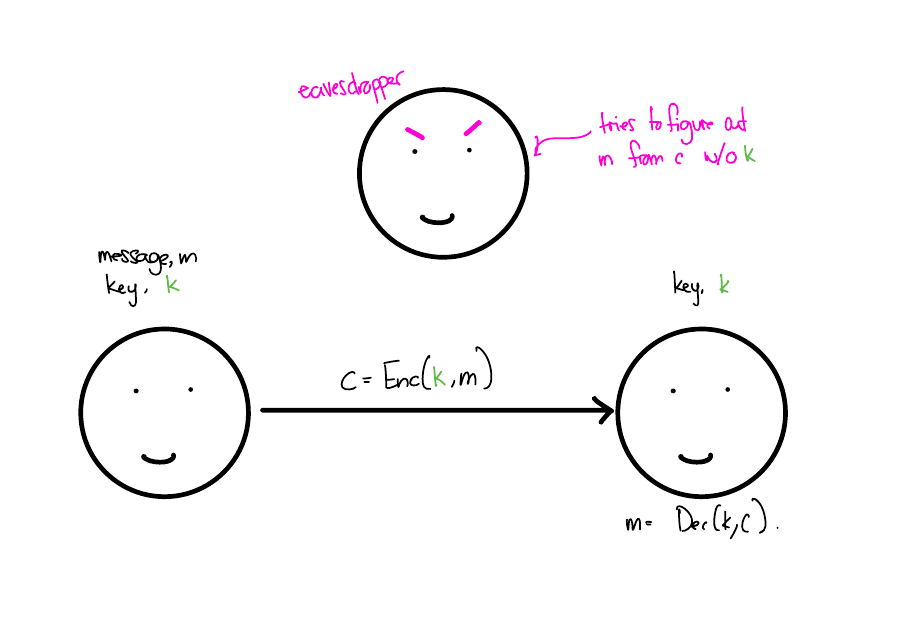
Shift Cipher
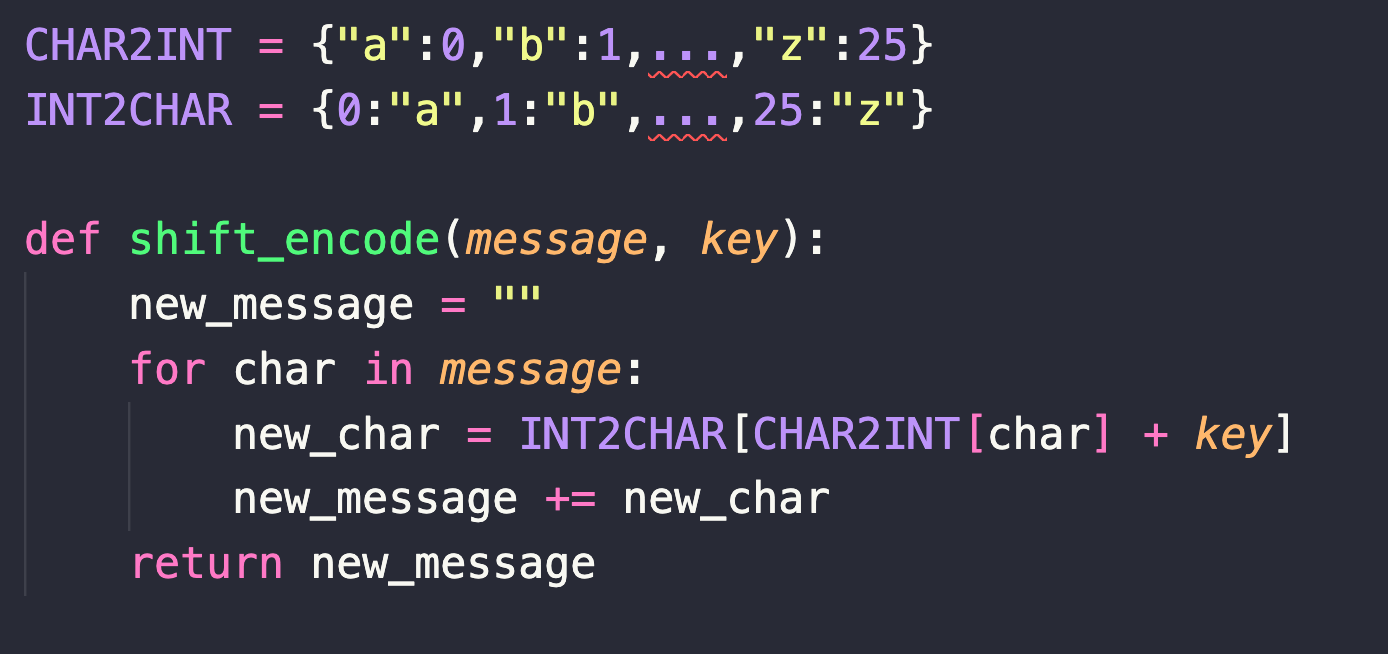
\[ \begin{align*} m = \texttt{hello}, k=3 \\ c = \texttt{jhoor} \end{align*} \]
Shift Cipher is not great
Suppose some eavesdropper who doesn’t know the key saw the ciphertext jhoor. What can they learn about the message?
Solution
They actually get to learn a lot about the message! For example, they know that the third and fourth character must have been the same in the message and can rule out messages like \(\texttt{peach}\). In fact, of all the \(26^5\) possible sequences of letters that could have been the message, they can narrow it down to just \(26\) possible messages.
For security, we want the eavesdropper to learn nothing about the real message!
Security
How can we mathematically define “learns nothing”?
Solution
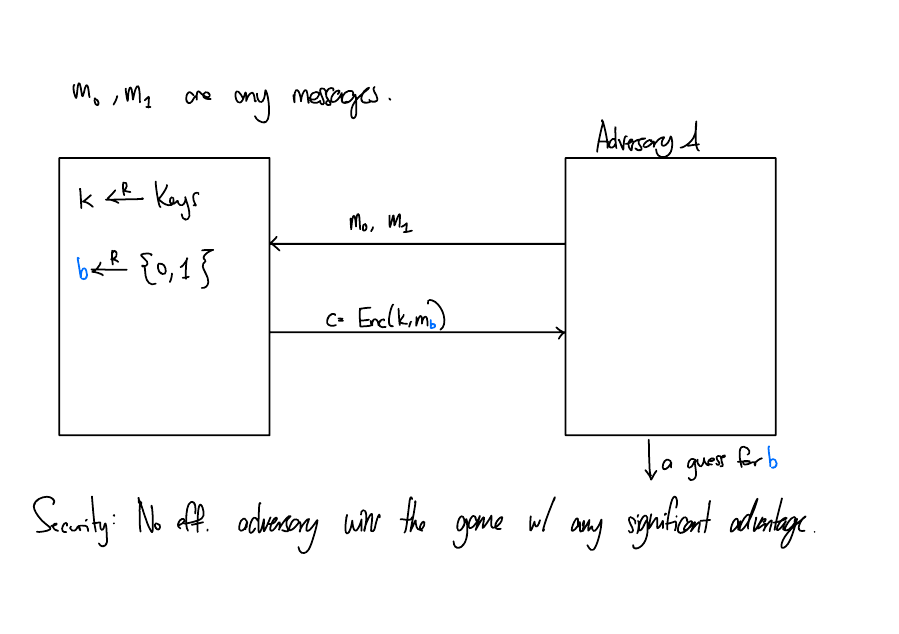
The assumptions - some problems are hard
Since we don’t have a way of checking all algorithms, we need to make some assumptions of the form: “There is no efficient algorithm to solve \(X\)” i.e. \(X\) is a hard problem.
We then use problem \(X\) to design an encryption scheme. To prove the security of that scheme, we prove that if there is an adversary that can distinguish b/w the encryption of two messages, then they can solve problem \(X\) efficiently, which is impossible under our assumption.
What are some hard problems you know that can be used?
Factoring large number is a common one. Finding the discrete logarithm is another.
Interestingly, these problems are not hard if there are good enough quantum computers : )
Cool things you can theoretically do
Zero Knowledge Proofs
Secret Sharing
Private Information Retrieval
Homomorphic Encryption
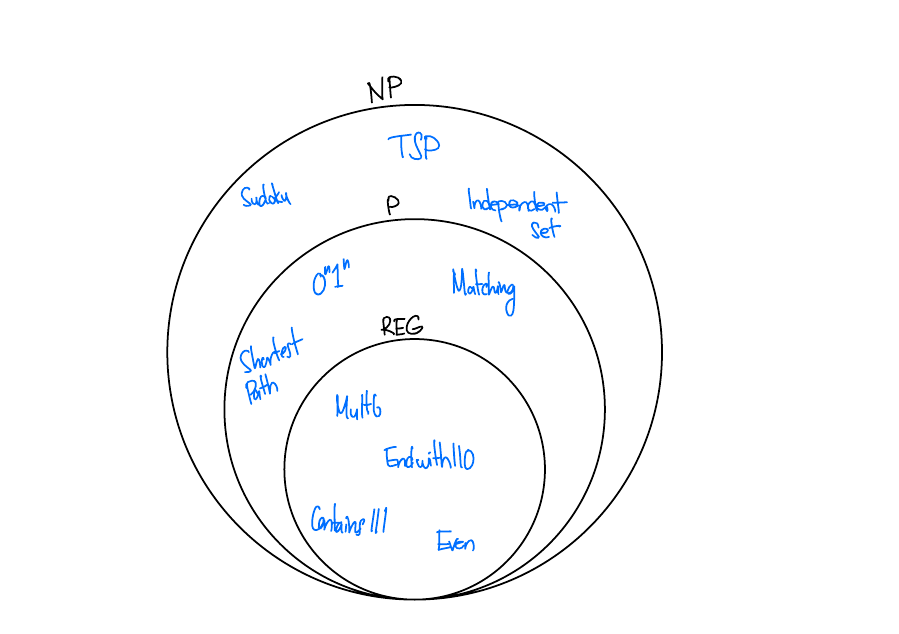
Complexity Theory
Resources
We looked at time as a valuable resource for computation. What are some other resources you can think of?
Once we pick a resource R, we can ask...
How much R do we need to solve problem \(X\)?
Exchange rates?
How much extra time do I need to simulate random or nondeterministic computation?
How much time can I buy with extra space?
The Power of Nondeterminism
For DFAs, we saw that adding nondeterminism gave us no additional power.
We can simulate a NFA using a DFA!
An analogous fact is not known for more general computation.
P and NP
\(P\) is the set of formal languages that can be solved deterministically in polynomial time.
\(NP\) is the set of formal languages that can be solved nondeterministically in polynomial time.
NP
\(NP\) is equivalent to the set of formal langauge for which we can verify a solution to a problem deterministically in polynomial time.
For example,
\[ \mathrm{Sudoku} = \{S: S \text{ is a sudoku puzzle with a solution}\} \]
Given a sudoku puzzle \(S\), and proposed solution \(S'\), I can quickly check whether or not \(S'\) is indeed a solution for \(S\) and hence \(S \in \mathrm{Sudoku}\)
\(NP\) represents the class of problems we can reasonably hope to solve. If we can’t check whether a proposed solution is correct, how can I be confident about any answer?
Sudoku
Does this sudoku have a solution? 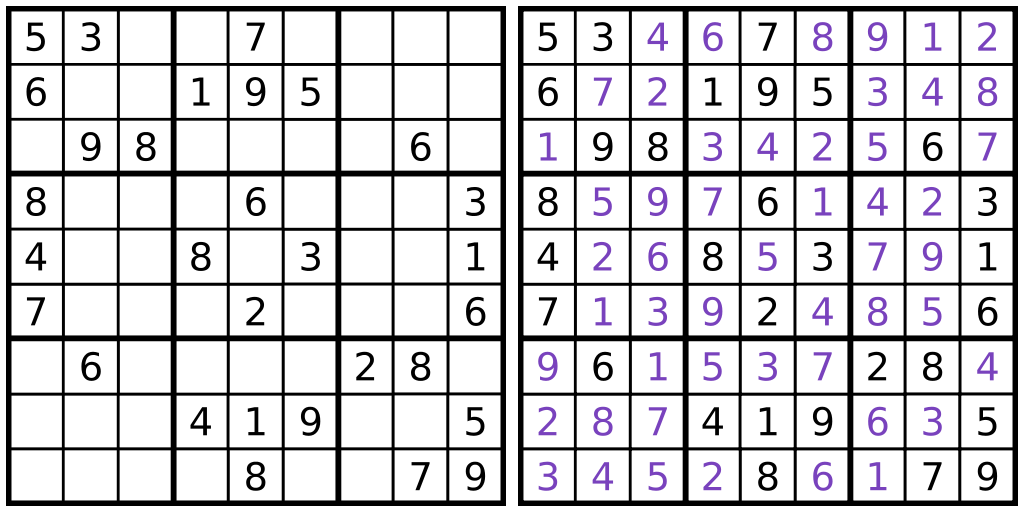
Is this a valid solution to the sudoku puzzle? 
Examples
Huge open problem
Is \(P = NP\)?
I.e. If I can check a solution to a problem deterministically in polynomial time, can I solve the problem deterministically in polynomial time?
Intuition: No! It’s much easier to check a solution than to solve the problem!
This is one of 7 Millennium Prize Problems. There is a 1000000 USD prize for each problem. So far, just one out of 7 of the problems have been solved.
Next steps
Depending what you liked here are some topics to explore next! If you liked...
Mathematical foundations...
MAT377 - Mathematical Probability
MAT344 - Introduction to Combinatorics
MAT332 - Introduction to Graph Theory
MAT221/223/224 - Linear Algebra
Algorithms...
CSC263 - Data Structures and Analysis
CSC373 - Algorithm Design, Analysis & Complexity
CSC473 - Advanced Algorithm Design
CSC324 - Principles of Programming Languages
Formal Languages...
CSC448 - Formal Languages and Automata
CSC463 - Computational Complexity and Computability
That’s it!
It’s been a pleasure being your instructor this term! I hope you enjoyed the course.
Best of luck on the exam, and beyond!
CSC236 Summer 2025