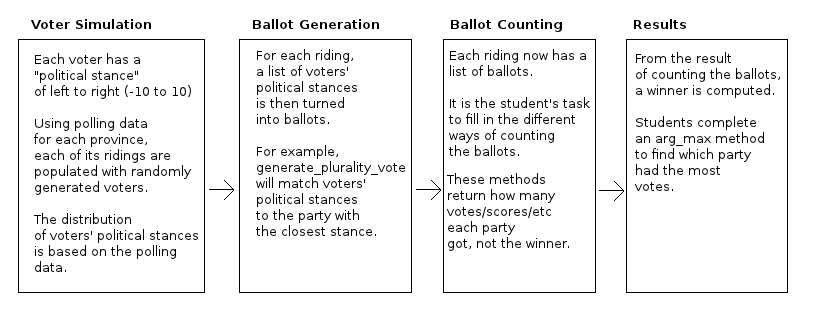
Simulating Canadian Elections!
Elizabeth Patitsas
June 23, 2012
Assignment meta-info for
instructors
In this assignment, we will be getting practice with lists, and to a
smaller extent, dictionaries. Students are expected to be familiar
with both, such as in how to access elements, iterate over them,
etc. The assignment assumes students are familiar with iteration,
conditionals, creating functions, passing functions as parameters
(though only in one place), and seeding random number generators.
The assignment does not assume students have experience with OOP or
file IO, making it appropriate for an Objects-Later course like CSC
108.
The Assignment
Voting theory is the study of voting systems -- different
algorithms for computing a "winner" given a list of candidates and a
list of voters. In this assignment, we will simulate several
different voting systems in the context of Canadian elections.
You are probably familiar with Plurality,
also known as First Past the Post. All the voters choose one and
only one candidate to vote for, and the candidate with the most
votes is elected.
Another way is Approval Voting
-- the voters vote for as many candidates as they approve of. Or,
instead, in a system called Range
Voting, voters could give each candidate a score between 1
and 5, and the candidate with the highest score wins.
There are dozens of different voting systems -- in this assignment,
we'll be looking at seven:
- Plurality,
the system we use here in Canada, the United Kingdom, and the
United States.
- Approval
Voting, used on many websites with a focus on
user-generated content.
- Range
Voting, which is used all over the place, though not
commonly in politics.
- The Borda
Count, often used in sports competitions.
- Instant
Run-Off Voting, used in India, Ireland, and other
jurisdictions throughout the world. The Liberal Party of Canada
also uses this system to elect their leader.
- The
D'Hondt Method, the most commonly used form of
proportional representation (per Wikipedia, it is used in
Albania, Argentina, Austria, Belgium, Brazil, Bulgaria,
Cambodia, Cape Verde, Colombia, Croatia, Czech Republic,
Denmark, East Timor, Ecuador, Estonia, Finland, Guatemala,
Hungary, Iceland, Israel, Japan, Luxembourg, Republic of
Macedonia, Republic of Moldova, Montenegro, the Netherlands,
Northern Ireland, Paraguay, Poland, Portugal, Romania,
Scotland, Serbia, Slovenia, Spain, Turkey, Uruguay and Wales.)
- The
Single Transferable Vote, which is used in Australia, and
was proposed for
use in British Columbia.
The first five systems are examples of single-winner elections -- each election
produces one and only one winner. So, in a House of Commons where
there are 308 seats, a total of 308 elections are held, one for
each riding. The other two systems are proportional representation systems; instead of
one-MP-per-riding, we will instead elect four MPs to 77
mega-ridings.
A Brief Introduction to Canadian
Politics
Canada's House of Commons is the elected body in the Canadian
Parliament. The country is divided into 308 constituencies, better
known as "ridings." Each riding elects a Member of Parliament (MP)
to the House of Commons using Plurality (a.k.a. First Past the
Post). The party with the most MPs forms the government, and the
party's leader becomes the Prime Minister. As such, Canadians do
not vote directly for the Prime Minister.
At present, there are five parties represented in the House of
Commons (with the following colour scheme):
- the Conservatives
(right-wing)
- the Liberals
(centre)
- the New Democratic
Party (left-wing)
- the Green Party
(environmentalist)
- and the Bloc Québécois (Québec
sovereigntist). The BQ is absent from this simulation as it only
runs candidates in Québec.
The Conservative Party of Canada is shortened as "CPC" in
variable names, and the New Democratic Party is shortened to
"NDP."
For the simulation, each party and each voter has a "political
stance", a number from -10 to 10, where a -10 is left-wing, and 10
is right-wing. We did this to account for the relative distances
between the parties -- we averaged the left/right and
authoritarian/libertarian values from the Political Compass'
analysis of the
last Canadian election. So for this simulation, the
Conservatives' political stance is a 6.5, since they are at (7,6)
on the Political Compass.
This assignment assumes no further knowledge of the Canadian
system.
The Structure of this Assignment
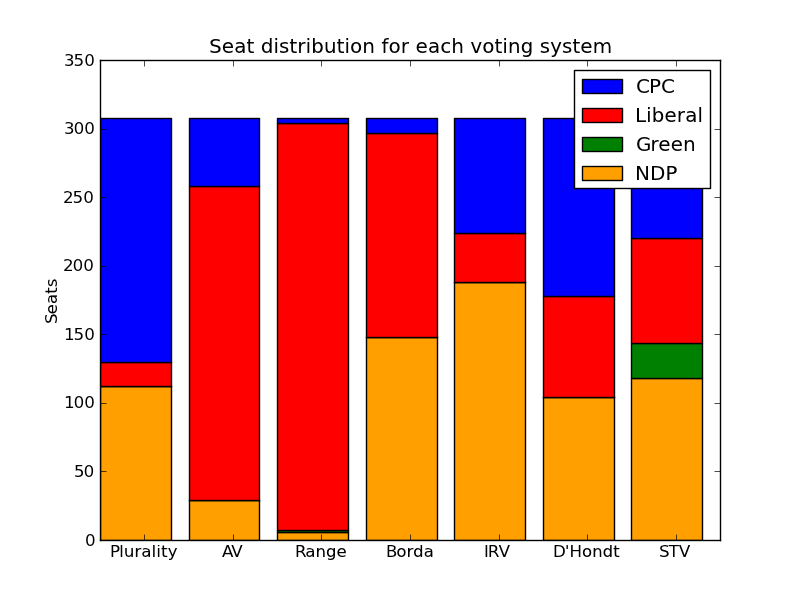
The different voting systems will produce different results. Based
on the most recent polling data from Harris-Decima, the results look
like this:
A Note on the Simulation
This simulation, like all models, is only as good as the
assumptions which underlie it. The methods we have provided to
simulate random voters are far from perfect -- our goal was only
to make them plausible.
We have also made a few simplifications in our model. For one,
there are only four parties: the NDP, the Greens, the Liberals,
and the Conservatives. We apologize to the Bloc
Québécois and the other parties not represented
here. Our simulation doesn't support differences between provinces
-- we just have random "ridings", each with a different
distribution of voter political beliefs. Advanced simulations of
Canadian elections have detailed data on each of the 308 ridings
in the country, data on provincial trends, and empirical support
from polling Canadians -- and even these simulations cannot see
the future. Parties change, candidates rise and fall, and voters
change their beliefs. But voting systems are algorithms -- and
these algorithms are the focus of this assignment.
Getting Started
Download the files voting_simulation.py
and voter_generation.py. You
will be filling in the code in voting_simulation.py; you will not
need to make any changes to voter_generation.py.
Your tasks in completing the file voting_simulation.py are:
- Complete the function arg_max(my_list)
The purpose of this function is to return the index of the
largest element in the list my_list. So, for the list [23, 0,
100, 23], the largest element is 100, and the argmax is 2. In
the event of a tie, choose randomly.
This function is used to calculate the winner of a Plurality
election -- you'll see the function voting_plurality returns how
many voters vote for each party, but not which party won the
election in that riding. First you should test it with test_arg_max(), and you are
encourage to add any other test cases you wish. You should get:
0 ; should be 0
4 ; should be 4
2 ; should be 0 or 2
2 ; should be 0 or 2
[247, 261, 252, 240] ;
should be about [250, 250, 250, 250]. I get [247, 261, 252,
240].
From there, try running election(voting_plurality,
200, 1), which simulates a plurality election with 200
voters in each riding. The 1 is the random seed for the
election, so that each time you rerun the code it will behave
the same way (this helps with debugging!). You should get a
result like:
[21364, 3205, 15875,
21156] -- the popular vote
[130, 0, 3, 175] -- the
seats assigned
In this plurality election, the Tories will form a government
with 175 seats, the Liberals are demolished, and the NDP forms
the opposition with 130 seats. A property of plurality
elections, known as Duverger's
Law, finds that over time, plurality systems become
two-party systems. Why do you think this is?
- Complete the function voting_approval
This function simulates an election with Approval Voting.
Have a look at voting_plurality to see how one voting system
looks. The two will have a lot in common -- for each voter in
list_voters, you'll want to generate a vote for them. Here,
you'll want to use generate_av_vote, which returns a list.
For example, if generate_av_vote returns [1,1,1,0] it means that
voter is voting for the NDP, Greens and Liberals, but not the
Conservatives.
Similar to voting_plurality, this function should return the
party-by-party total for the riding. So, if there are 23 votes
for the NDP, 0 for the Greens, 100 for the Liberals, and 23 for
the Conservatives, it should return the list [23, 0, 100, 23].
You can test your code with test_voting_approval,
which will get you:
[1, 1, 0, 0] ; should be
[1,1,0,0]
[10, 10, 10, 0] ; should
be [10,10,10,0]
[809, 515, 1246, 2193] ;
should be about [~805, ~492, ~1224, ~2212]
[1000, 1000, 118, 1000] ;
should be about [1000, 1000, ~121, 1000]
From there, try print
election(voting_approval, 200, 1). You should get
output like:
[29480, 24430, 34370,
26997] -- the popular vote
[20, 0, 236, 52] -- the
seats assigned
Ensure that this code works for other random seeds. Note that
seed 0 will always produce the same voter preferences --
voting_approval is producing a very different result than
voting_plurality despite having the same voters in it. Here the Liberals do well
and form a strong majority -- in Plurality, it was the NDP and
Conservatives that won with the same electors.
Also note that the popular vote here is different, since voters
could vote for as many parties as they wanted. How does this
seat distribution correspond to the popular vote? Better or
worse than Plurality?
- Complete the function voting_range
Here we're doing the same thing, but with Range Voting. Voters'
ballots should be generated with generate_scored_vote(), which
will give each party a score 1-5, where a 1 means the voter
opposes that party, and a 5 means the voter supports the party.
First do our usual test test_voting_range, then try the election(voting_range, 200, 1)
code. You should get a result like:
[163332, 166918, 190857,
148065] -- popular vote
[1, 0, 307, 0] -- seat
assignments
Here the Liberals come out even more triumphant, with a
landslide victory! But how does this compare to the popular
vote, which here is the sum of voters' scores for each party?
Ensure that this code works for other random seeds.
- Next up is voting_borda
The Borda Count uses ranked ballots, rather than giving
candidates scores or the like. Here, voters need to put down the
order in which they prefer the four parties. You can get ranked
ballots from generate_ranked_vote(voter). It will give you a
list with a given voter's ordering of the parties. For example,
a voter who prefers the Conservatives the most, followed by the
Greens, then Liberals, then NDP, will be represented by the list
[3,1,2,0].
The way the Borda Count works, a voter's first choice gets n-1 points (where n is the
number of candidates). Their second choice gets n-2 points. Their third
choice gets n-3
points. And so on. So in our example, the Conservatives would
get 3 points, Greens get 2 points, Liberals get 1, and the NDP
doesn't get any.
Then we sum up which party has the most points overall.
Again, we have provided you with some test cases in
test_voting_borda, and then
election(voting_borda, 200, 1). It gives a result
like:
[105019, 81313, 104201,
79067] -- popular vote
[153, 0, 142, 13] -- seats
assigned
Here we see a minority government for the NDP! Would you expect
an NDP landslide given the popular vote?
Don't forget to ensure that your code works for other random
seeds!
- The Borda count is far from the only system which uses ranked
ballots -- The Instant Run-Off Vote (voting_irv) is another. It works like this:

Here, you will want to keep track of all the different orderings
of the parties, and how popular each different ordering is. (Hint: use a dict to keep track of
the different orderings and their frequencies!)
We have provided the helper function arg_min_nozero, to identify
which party should be eliminated in a given run-off.
As usual, test your code with test_voting_irv() and the provided call to
election.
Like the Borda Count, this gives a majority for the NDP. Why
does the popular vote correspond better to the seat allocation
than the Borda Count?
Don't forget to ensure that your code works for other random
seeds!
- We're now ready to implement our first proportional
representation method, the D'Hondt Method.
In previous voting systems, we always returned how many
votes/points/etc each party had for one riding, and that riding
elected the party which had the most of those. This will be
different.
Here, we will get a list_voters which spans four ridings, and we
will elect four MPs to to this "mega-riding". The function will
return what parties those MPs belong to -- for instance [2, 0,
1, 1] means that two NDP MPs have been elected, one Liberal, and
one Conservative.
To see how this method works, see here: The
D'Hondt Method.
Use test_voting_dhondt to
get you started, and then the next call to election.
While not shown here, the popular vote would be the same as for
Plurality ([21364, 3205,
15875, 21156]) -- since we are using the same random
seed, our voters will have done the same voting as in that
simulation. A property of the D'Hondt Method as a form of
proportional representation since it has a bias towards large
parties -- do we see this bias here?
Don't forget to ensure that your code works for other random
seeds!
- And, finally, an essay question. Which voting system do you think is best and why?
Which of the seven systems here best matches up to the popular
vote? What are the advantages and advantages of each?
A common complaint about the current system is the sense that
one's vote "does not matter." Do you think this is true about
Plurality? Do the other voting systems rectify this problem?
Hand in your code, and your essay. We will be testing your code
with a seed other than 0, so ensure your code works with any seed!
***
Challenge question (difficult, for bonus marks):
- Finally, we turn to the Single
Transferable Vote. Like for the D'Hondt method, we will
amalgamate every four ridings into "mega-ridings" and elect four
MPs for each "mega-riding".
This method is similar to Instant Run-Off Voting in that voters
will rank candidates. If support for a given party exceeds what
we call the Droop Quota (provided to you as the helper function
droop_quota), that party gets a seat. Subtract the Droop Quota
from the number of votes that party has.
If all the parties are under the Droop Quota, eliminate the
party with the least support, and transfer their ballots to
their next-preferred party who is still in the race. Assess if
that puts any parties over the Droop Quota, and continue until
all four seats have been assigned. Note that in our version of
STV, since we vote for parties rather than candidates, a party
should be able to win multiple seats in the riding!


