Recurrent Neural Networks¶
Last time, before the midterm, we discussed using recurrent neural networks to make predictions about sequences. In particular, we treated tweets as a sequence of words. Since tweets can have a variable number of words, we needed an architecture that can take as input variable-sized inputs.
The recurrent neural network architecture looked something like this:
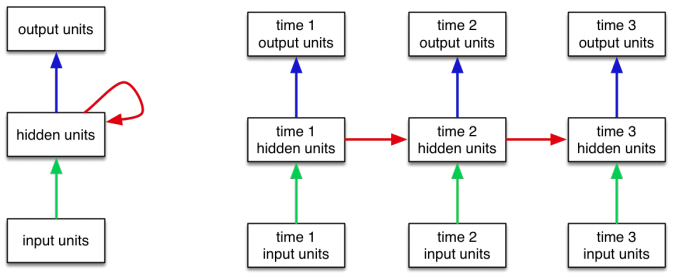
We briefly discussed how recurrent neural networks can be used to generate sequences. Generating sequences is more involved compared to making predictions about sequences. However, many students chose text generations problems for their project, so a brief discussion on generating text might be worthwhile.
Much of today's content is an adaptation of the "Practical PyTorch" github repository [1].
[1] https://github.com/spro/practical-pytorch/blob/master/char-rnn-generation/char-rnn-generation.ipynb
Preparing the Data Set¶
We will begin by choosing some text to generate. Since we are already working "SMS Spam Collection Data Set" [2], we will build a model to generate spam SMS text messages.
[2] http://archive.ics.uci.edu/ml/datasets/SMS+Spam+Collection
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
We are going to start by doing something a little strange: we are going to concatenate all spam messages into a single string. We will sample random subsequences (chunk) from the combined string containing all spam messages.
This technique makes less sense when we use short strings like SMS text messages, but makes more sense we are working with sequences that are much longer than the random subsequence samples (chunk) -- for example if we trained on news articles, Wikipedia pages, Shakespeare plays, or TV scripts. In all cases, the probability of choosing a chunk that contains text from two samples will be small.
In our case, we could do better than combining all training text into one string. For simplicity, however, we won't.
spam_text = ""
for line in open('SMSSpamCollection'):
if line.startswith("spam"):
spam_text += line.split("\t")[1].strip("\n")
# show the first 100 characters
spam_text[:100]
Since we are working with SMS text messages, we will use a character-level RNN. The reason is that spammy SMS messages will contain not only words, but abbreviations, numbers and other non-word characters.
We find all the possible characters in spam_text, and build dictionary mappings
from the character to the index of that character (a unique integer identifier),
and from the index to the character. We'll use the same naming scheme that torchtext
uses (stoi and itos).
vocab = list(set(spam_text))
vocab_stoi = {s: i for i, s in enumerate(vocab)}
vocab_itos = {i: s for i, s in enumerate(vocab)}
len(vocab)
There are 94 unique characters in our training data set.
Now, we'll write a function to select a random chunk. Each time we need a new
training example, we will call random_chunk() to obtain a random subsequence
of spam_text.
import random
random.seed(7)
spam_len = len(spam_text)
def random_chunk(chunk_len=50):
"""Return a random subsequence from `spam_text`"""
start_index = random.randint(0, spam_len - chunk_len)
end_index = start_index + chunk_len + 1
return spam_text[start_index:end_index]
print(random_chunk())
print(random_chunk())
Since we will use one-hot embedding to represent each character, we need to look up the indices of each character in a chunk. We will also combine the indicies of each character into a tensor.
def text_to_tensor(text, vocab=vocab):
"""Return a tensor containing the indices of characters in `text`."""
indices = [vocab_stoi[ch] for ch in text]
return torch.tensor(indices)
print(text_to_tensor(random_chunk()))
print(text_to_tensor(random_chunk()))
We will use these tensors to train our RNN model. But how?
At a very high level, we want our RNN model to have a high probability of generating the text in our training set. An RNN model generates text one character at a time based on the hidden state value. We can check, at each time step, whether the model generates the correct next character. That is, at each time step, we are trying to select the correct next character out of all the characters in our vocabulary. Recall that this problem is a multi-class classification problem.
However, unlike multi-class classification problems with fixed-sized inputs, we need to keep track of the hidden state. In particular, we need to update the hidden state with the actual, ground-truth characters at each time step.
So, if we are training on the string RIGHT, we will do something like this:
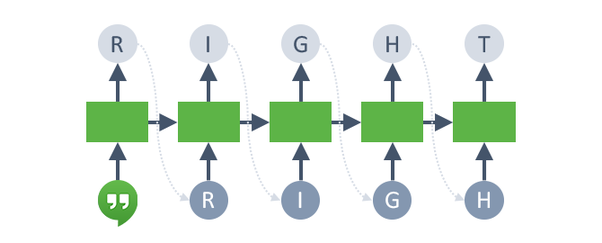
We will start with some sequence to produce an initial hidden state (first green box from the left), and the RNN model will make a prediction on what letter should appear next.
Then, we will feed the correct letter "R" as the next token in the sequence, to produce a new hidden state (second green box from the left). We use this new hidden state to predict what letter should appear next.
Again, we will feed the correct letter "I" as the next token in the sequence, to produce a new hidden state (third green box from the left). We continue until we exhaust the entire sequence.
In this example, we are (somewhat simultaneously) solving many different multi-class classification problems. We know the ground-truth answer for those all problems, meaning that we can use a cross-entropy loss and the usual optimizers to train our recurrent neural network weights.
To set our data up for training, we will separate the input sequence (bottom row in the above diagram) and the target output sequence (top row in the above diagram). The two sequences are really just offset by one.
def random_training_set(chunk_len=50):
chunk = random_chunk(chunk_len)
inp = text_to_tensor(chunk[:-1]) # omit the last token
target = text_to_tensor(chunk[1:]) # omit the first token
return inp, target
random_training_set(10)
The RNN Model¶
We are ready to build the recurrent neural network model. The model
has two main trainable components, an RNN model (in this case, nn.LSTM)
and a "decoder" model that decodes RNN outputs into a distribution
over the possible characters in our vocabulary.
class SpamGenerator(nn.Module):
def __init__(self, vocab_size, hidden_size, n_layers=1):
super(SpamGenerator, self).__init__()
# RNN attributes
self.vocab_size = vocab_size
self.hidden_size = hidden_size
self.n_layers = n_layers
# identiy matrix for generating one-hot vectors
self.ident = torch.eye(vocab_size)
# recurrent neural network
self.rnn = nn.RNN(vocab_size, hidden_size, n_layers, batch_first=True)
# a fully-connect layer that decodes the RNN output to
# a distribution over the vocabulary
self.decoder = nn.Linear(hidden_size, vocab_size)
def forward(self, inp, hidden):
# reshape the input tensor to [1, seq_length]
inp = inp.view(1, -1)
# generate one-hot vectors from token indices
inp = self.ident[inp]
# obtain the next output and hidden state
output, hidden = self.rnn(inp, hidden)
# run the decoder
output = self.decoder(output.squeeze(0))
return output, hidden
def init_hidden(self):
return torch.zeros(self.n_layers, 1, self.hidden_size)
model = SpamGenerator(len(vocab), 128)
Training the RNN Model¶
Before actually training our model, let's go back to the figure from earlier, and write code to train our model for one iteration.

First of all, we can generate some training data. We'll use a small chunk size for now.
chunk_len = 20
inp, target = random_training_set(chunk_len)
Second of all, we need a loss function and optimizer. Since we are performing multi-class classification for each character we wish to produce, we will use the cross entropy loss.
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
Now, we will perform the first classification problem (the second column in the figure). We start with a new hidden state (of all zeros):
hidden = model.init_hidden()
Then, we will feed the next token to the RNN, producing an output vector
and a new hidden state.
output, hidden = model(inp[0], hidden)
We can compute the loss using criterion. Since the model is untrained,
the loss is expected to be high. (For now, we won't do anything
with this loss, and omit the backward pass.)
criterion(output, target[0].unsqueeze(0))
With our new hidden state, we can solve the problem of predicting the next token;
output, hidden = model(inp[1], hidden) # predict distribution of next token
criterion(output, target[1].unsqueeze(0)) # compute the loss
We can write a loop to do the entire computation. Alternatively, we can simply call:
hidden = model.init_hidden()
output, hidden = model(inp, hidden) # predict distribution of next token
criterion(output, target) # compute the loss
Generating Text¶
Before we actually train our RNN model, we should talk about how we will actually use the RNN model to generate text. If we can generate text, we can make a qualitative asssessment of how well our RNN is performing.
The main difference between training and test-time (generation time) is that we don't have the ground-truth tokens to feed as inputs to the RNN. Instead, we will take the output token generated in the previous timestep as input.
We will also "prime" our RNN hidden state. That is, instead of starting with a hidden state vector of all zeros, we will feed a small number of tokens into the RNN first.
Lastly, at each time step, instead of always selecting the token with the largest probability, we will add some randomness. That is, we will use the logit outputs from our model to construct a multinomial distribution over the tokens, and sample a random token from that multinomial distribution.
One natural multinomial distribution we can choose is the distribution we get after applying the softmax on the outputs. However, we will do one more thing: we will add a temperature parameter to manipulate the softmax outputs. We can set a higher temperature to make the probability of each token more even (more random), or a lower temperature to assighn more probability to the tokens with a higher logit (output). A higher temperature means that we will get a more diverse sample, with potentially more mistakes. A lower temperature means that we may see repetitions of the same high probability sequence.
def evaluate(model, prime_str='win', predict_len=100, temperature=0.8):
hidden = model.init_hidden()
prime_input = text_to_tensor(prime_str)
predicted = prime_str
# Use priming string to "build up" hidden state
for p in range(len(prime_str) - 1):
_, hidden = model(prime_input[p], hidden)
inp = prime_input[-1]
for p in range(predict_len):
output, hidden = model(inp, hidden)
# Sample from the network as a multinomial distribution
output_dist = output.data.view(-1).div(temperature).exp()
top_i = int(torch.multinomial(output_dist, 1)[0])
# Add predicted character to string and use as next input
predicted_char = vocab_itos[top_i]
predicted += predicted_char
inp = text_to_tensor(predicted_char)
return predicted
print(evaluate(model, predict_len=20))
It is hard to see the effect of the temperature parameter with
an untrained model, so we will come back to this idea after training
our model.
Training¶
We can put everything we have done together to train the model:
def train(model, num_iters=2000, lr=0.004):
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()
for it in range(num_iters):
# get training set
inp, target = random_training_set()
# cleanup
optimizer.zero_grad()
# forward pass
hidden = model.init_hidden()
output, _ = model(inp, hidden)
loss = criterion(output, target)
# backward pass
loss.backward()
optimizer.step()
if it % 200 == 199:
print("[Iter %d] Loss %f" % (it+1, float(loss)))
print(" " + evaluate(model, ' ', 50))
train(model)
Gated Recurrent Units¶
Last time, we discussed the Long Short-Term Memory (LSTM) model
nn.LSTM as an alternative to nn.RNN. We did not use nn.LSTM
since the nn.LSTM model requires both a hidden and a cell-state.
We can switch our model to use nn.LSTM if we want to, and
obtain a better performance.
Instead, there is another RNN model we could use called the
"Gated Recurrent Unit" nn.GRU. This is a newer model than the LSTM,
and a smaller model that uses some of the key ideas of the LSTM.
Like the LSTM,
GRU units are also capable of learning long-term dependencies.
GRU units perform about as well as the LSTM, but does not have the
cell state.
In our code, we can swap in the nn.GRU unit in place of the nn.RNN
unit. Let's make the swap. We should see a performance boost.
class SpamGenerator(nn.Module):
def __init__(self, vocab_size, hidden_size, n_layers=1):
super(SpamGenerator, self).__init__()
# RNN attributes
self.vocab_size = vocab_size
self.hidden_size = hidden_size
self.n_layers = n_layers
# identiy matrix for generating one-hot vectors
self.ident = torch.eye(vocab_size)
# recurrent neural network
self.rnn = nn.GRU(vocab_size, hidden_size, n_layers, batch_first=True)
# a fully-connect layer that decodes the RNN output to
# a distribution over the vocabulary
self.decoder = nn.Linear(hidden_size, vocab_size)
def forward(self, inp, hidden):
# reshape the input tensor to [1, seq_length]
inp = inp.view(1, -1)
# generate one-hot vectors from token indices
inp = self.ident[inp]
# obtain the next output and hidden state
output, hidden = self.rnn(inp, hidden)
# run the decoder
output = self.decoder(output.squeeze(0))
return output, hidden
def init_hidden(self):
return torch.zeros(self.n_layers, 1, self.hidden_size)
model = SpamGenerator(len(vocab), 128)
train(model, num_iters=5000)
Temperature¶
Now let's look at the effect of temperature. We'll start with a very low temperature:
for i in range(10):
print(evaluate(model, ' ', 50, temperature=0.2))
Notice how we get fairly good samples, but they are all very similar to each other.
If we increase the temperature, we get more diverse sequences. However, the quality of the samples are not as good:
for i in range(10):
print(evaluate(model, 'win', 50, temperature=0.8))
Finally, if we increase the temperature too much, we get very diverse samples, but the quality becomes increasingly poor.
for i in range(10):
print(evaluate(model, 'win', 50, temperature=1.2))
If we increase the temperature enough, we might as well generate random sequences.
for i in range(10):
print(evaluate(model, 'win', 50, temperature=3))