Introduction to Sorting

Here we consider algorithms to sort a shuffled list of items.

We will assume that our list is stored in an array of Comparable objects. Our task is to rearrange the items in the list so that they appear in non-decreasing order. Moreover, we are going to do this rearranging using the compareTo method. These algorithms are called "comparison sorts" (see Wikipedia).

We consider big-Oh runtimes for several different comparison sorting algorithms. In all cases we assume the method compareTo runs in a bounded amount of time (i.e., it is O(1)).

For a Java demo of various sorting algorithms, see Jason Harrison's sorting demo page.

Selection Sort

The following algorithm grows a sorted sublist within the current array by selecting the smallest item of all remaining items, and placing it at the end of the sorted sublist. Here is the selection sort algorithm:

1. Find the minimum value in the list, and swap this with the front of the list.
2. Then find the minimum value in the "remaining items" (i.e., the 2nd item through to the last item), and swap this with the second item in the list.
3. Continue until the second largest item is moved.

  [ 7, 5, 2, 4 ]


  [ 2, 5, 7, 4 ]  // Underline denotes 
   --             // sorted sublist

  [ 2, 4, 7, 5 ]
   -----

  [ 2, 4, 5, 7 ]
   ------------

  public static void selectionSort(Comparable list[]) {
    int n = list.length;
    for (int k = 0; k < n - 1; k++ ) {
      // Find the smallest item in the remaining n-k items.
      Comparable minVal = list[k];
      int kMin = k;
      for (int j = k + 1; j < n; j++) {
        if (minVal.compareTo(list[j]) > 0) {
          minVal = list[j];
          kMin = j;
        }
      }
      // Swap the minimum value into location k
      list[kMin] = list[k];
      list[k] = minVal;
    }
  }

Analyzing the runtime of the loops in this method from the inside out, we find:

1. The body of the inner-most loop runs in constant time, bounded by K, say.
2. The inner-most loop runs n-(k+1) times, and takes O(1) time to initialize. So the total time for this loop is (n-k-1)K + O(1).
3. The outer-most loop executes in the time it takes to execute the inner-most loop plus O(1), which is again (n-k-1)K + O(1) time.
4. The outer-most loop is executed for k = 0, 1, ... n-2, so the total time for the outer-most loop is:

     T = [(n-1) + (n-2) + ... + 1]K + n O(1)
   

   The sum of integers from 1 to n-1 is just (n-1)n/2 (see Wikipedia), which is O(n^2). So T is O(n^2).
5. Finally the setup for the outer loop, and the method return both take O(1) time. So the total time is T + O(1).

A similar anaylsis shows that this algorithm uses O(n^2) compareTo method calls.

Bubble Sort

BubbleSort successively sweeps through the array of items, swapping any items which are out of order. After the first sweep, the largest item will end up at the end of the array. (Why?) The second sweep will then place the second largest item in the correct position. The algorithm repeats these sweeps but, instead of sweeping to the end of the array each time, each sweep is terminated at the last item swapped in the previous sweep. Trace a short example.

  [ 7, 5, 2, 4 ]
                 // after one sweep...

  [ 5, 2, 4, 7]  // Underline denotes 
            --   // sorted sublist

  [ 2, 4, 5, 7 ]
         ------

  [ 2, 4, 5, 7 ]
   ------------

Here is the Java code (see Sorting.zip):

  public static void bubbleSort(Comparable list[]) {
    int n = list.length;
    int lastSwap = n-1;
    while (lastSwap > 0) {
      // Sweep through items 0 .. lastSwap-1, swapping
      // any out of order items.
      int jSwap = -1;
      for (int j = 0; j < lastSwap; j++) {
        Comparable bubble = list[j];
        if (bubble.compareTo(list[j+1]) > 0) {
          list[j] = list[j+1];
          list[j+1] = bubble;
          jSwap = j;
        }
      }
      lastSwap = jSwap;
    }
  }

What is the runtime order?

The body of the inner loop takes bounded time, say less than K operations (we are assuming the compareTo calls are O(1)). Therefore the inner-most loop runs in time K lastSwap + O(1). In the worst case, lastSwap decreases by one each iteration, so the outer loop is executed for lastSwap = n-1, n-2, ... 1. The worst-case running time is therefore

  T = [(n-1) + (n-2) + ... + 1] K + O(n)

A similar anaylsis shows that this algorithm uses O(n^2) compareTo method calls.

Therefore the selectionSort and bubbleSort algorithms have the both have an O(n^2) runtime, and both call the compareTo() method O(n^2) times (in the worst-case). So we cannot choose between these two methods without doing a more detailed analysis or by running some timing experiments.

Testing the Algorithms and Measuring the Runtimes

The zip file Sorting.zip contains:

1. The ListUtil class which has the above sorting methods (plus two other methods discussed further below).
2. The JUnit class SortTest which provides some simple tests of the sorting methods.
3. The SortDriver class contains a main method which ouputs measured runtime information for each of the sorting algorithms.

The main method in SortDriver builds several lists, with lengths ranging between 1000 and 20,000 items. The runtimes for each of the sorting algorithms are measured for each of these lists. The results are written into a file sortTimes.txt. (We then read this file with a Matlab program named runTimeScript.m and plot the data.)

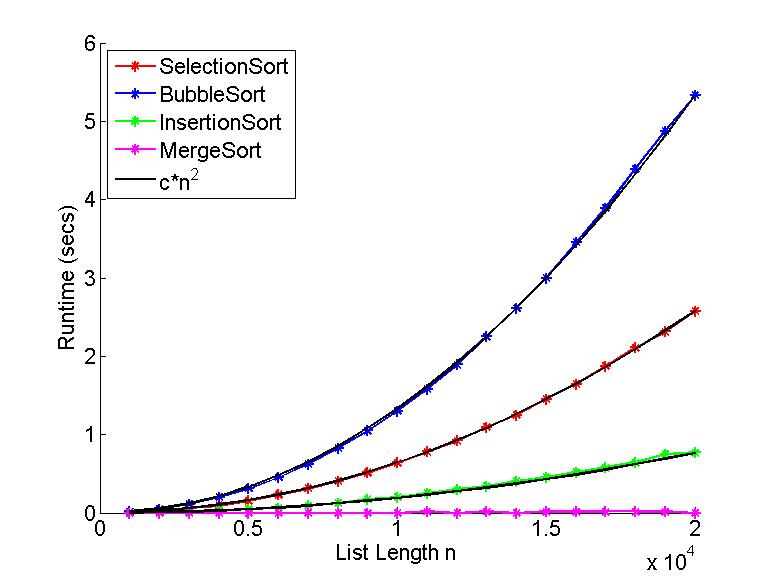
The results are shown below:

The implementation of bubble sort is seen to be about twice as slow as selection sort. The other two sorting algorithms are faster still, and we will discuss them further below.

It is useful to try modelling the shape of these curves (for large enough list lengths). Our analysis above indicated their runtimes were O(n^2) so, by the definition of O(.), they have to be bounded by c*n^2 for n >= B, for some constants c and B.

In the above plot we are also plotting t(n) = d * n^2 (in black), where the constant d is chosen such that t(20000) is the runtime observed for the largest list length. This allows us to informally compare the shape of the graph of measured runtimes with a monomial of the form d*n^2.

The agreement between the measured times and the monomials is remarkable. Our big-Oh bounds appear to be tight.

How Many Comparisons are Necessary?

How fast can we sort? Here's a nice example of lateral thinking.

Imagine playing 20 questions with this sorting problem. In this case, the list of targets is simply the list of all permutations of a list of length n. If we knew which permutation our given list was shuffled into, then we could undo it, and we would have a sorted list. So the problem, then, is a familiar one. How quickly can we zero in on the correct permutation within this meta-list of all possible permutations of lists of length n? Last day we said the best we could do with binary questions was to use binary search!

It doesn't matter exactly how we could use binary search, we are only interested in guessing the (worst-case) minimum number of comparison operations needed. What we are claiming is that this minimum number has to be at least the number of comparison operations needed to search the meta-list of all permutations using binary search. That should seem at least barely plausible (I do not intend to prove it here).

Previously, we showed binary search requires O(log(L)) comparison operations where L is the length of the list to be searched. For our current analysis, L is the list of all permutations of a list of length n. So L = n! (n factorial). By Stirling's formula (see Wikipedia) we have

  log(L) = nlog(n) + O(n)

This argument suggests that the minimum number of comparison operations we will need (in the worst-case) for any comparison sort algorithm is O(log(L)) = O(n log(n)).

The previous sorting algorithms both required O(n^2) compareTo operations. Can we dream up an algorithm which requires only O(n log(n))?

Binary Insertion Sort

Suppose we grow a sorted sublist in one portion of the array of list items, in the manner of selectionSort above. However, instead of finding the biggest element, suppose we just insert the next unsorted element into the sorted list. Trace a simple example:

  [ 7, 5, 2, 4 ] // Underline denotes 
   --            // sorted sublist               

  [ 5, 7, 2, 4]  
   ----- 

  [ 2, 5, 7, 4]
   --------

  [ 2, 4, 5, 7 ]
   ------------

If we use binary search to find where the new item should go, we use only O(log(m)) compareTo() operations to find the appropriate location, where m is the length of the sorted sublist. We need to do this for sublists of length 1, 2, 3, ... n-1. So the number of compareTo operations will be

  O(log(1) + log(2) + ... + log(n-1)) which is contained in O(nlog(n))

What is the runtime for the whole algorithm? Let us write the algorithm in Java and see.

Writing Binary Insertion Sort in Java

To implement insertion sort efficiently, we first need to write a binarySearch method which will only search the first k elements in the argument array. We have done that by adding a three argument binarySearch method to ListUtil (see the method call below).

The resulting insertion sort method is then (see Sorting.zip):

  public static void insertionSort(Comparable list[]) {
    int n = list.length;
    for (int k = 1; k < n; k++) {
      // Use binary search to locate where
      // list[k] should go in the sorted sublist,
      // consisting of list[0..k-1].
      int index = binarySearch(list, k, list[k]);
      if (index < 0)
        index = -(index + 1);
      // Move the sublist from index to k-1
      // up one index.
      Comparable tmp = list[k];
      for (int j = k; j > index; j--) {
        list[j] = list[j-1];
      }
      // Put the new item at the cleared index.
      list[index] = tmp;
    }
  }

The worst-case runtime of this method can be shown to be O(n^2) (see Exercise 1 below).

This result informally agrees with the measured runtimes plotted above. In order to better see the curvature of the runtime graph as the length of the list increases, we show a blow up of the low runtime region below:

Again the measured runtimes appear to be modelled reasonably well with a simple monomial of the form t(n) = d * n^2 (i.e., the black curve overlayed on the green points).

Note this implementation of insertion sort is considerably faster than the previous two sorting algorithms, even though they are all O(n^2) algorithms. (Their multiplicative constants "d" differ.)

Notice the inner-most loop of insertion sort is particularly simple. We can replace it with one call to the System.arraycopy() method. This should speed up insertionSort further. (See Exercise 2 below.)

What is the Minimum Worst-Case Runtime?

We showed above that we could reduce the number of compareTo method calls to O(n log(n)). However, insertion sort is still has a runtime of O(n^2). The reason for the difference is all the copying that we have to do in the inner-most loop of insertion sort.

Can we find a comparison sorting method which has a runtime of O(n log(n))?

It turns out there are such algorithms and, moreover, O(n log(n)) is the smallest worst-case runtime order for any comparison sort algorithm. For example, heap sort and merge sort have O(n log(n)) worst case runtimes. We will study them later in the course.

The java.util.Arrays class includes a static sort(Comparable[]) method which implements the merge sort algorithm. We have called this method in ListUtils. The measured runtimes are plotted in the mauve curve in the above plots. Actually, the runtime for this method was too short for our ElapsedTime class to even measure (for which anything smaller than about 0.01-0.02 of a second is suspect). We need to give it longer lists to work on (see Exercise 3 below). (For a teaser, on my machine, merge sort runs on lists of length 2 million in about 2 seconds. That's roughly the runtime of bubbleSort on a list of length 10,000, and insertionSort on a list of size 16,000.)

Exercises

1. In a similar manner to the runtime analysis of selection sort and bubble sort, show that the insertionSort algorithm implemented above has a worst-case runtime of O(n^2). Here the input list is length n, and we are assuming all compareTo method calls are O(1). (You will need to use the result in question 4 below.)
   
   
2. The inner-most loop in binary insertion sort simply shifts part of the sorted sub-list over by one index to make room for the next item to be inserted. Look up the method java.lang.System.arraycopy() in the Java API. Copy the insertionSort() method within the ListUtil class to a second method, named insertionSortAC(). Modify this copied method by replacing the inner-most for loop (which copies a portion of the sorted sub-list) with one call to arraycopy(). Modify the SortTest code to add a test of insertionSortAC(), and run JUnit. Modify the timing tests in SortDriver.java to also test the new insertionSortAC() method. Is it faster? The arraycopy method is still O(n). What is the order of the runtime of the insertionSortAC() method?
   
   
3. Comment out the calls to all other sorting methods besides merge sort in the SortDriver class (i.e., in the runTest(PrintWriter) method). Increase the size of the test lists until you can resolve the runtime of the mergeSort() method. Can you resolve the difference between runtimes which behave like O(n log(n)) and O(n)?
   
   
4. Prove O(n log(n)) is contained in O(n^2).
   
   
5. Prove O(n^2) is not contained in O(n).