The string girdling Earth problem and how it relates to tendon displacement

Students I mentor often ask "How much do I need to pull on a tendon?" if they want to know the range of a reasonable tendon displacement for a tendon-driven continuum robot. So, it is a question about a value, which should be used as a upper and lower bound. I usually proceed to explain a related problem, or to be more precise, introduce a mathematical puzzle.

String girdling Earth: A string is tightly wrapped around the equator of a perfectly spherical Earth. If the string should be raised 1 metre (3 ft 3 in) off the ground, all the way along the equator, how much longer would the string be?

To find the answer requires only basic geometry, as you can see on the image.

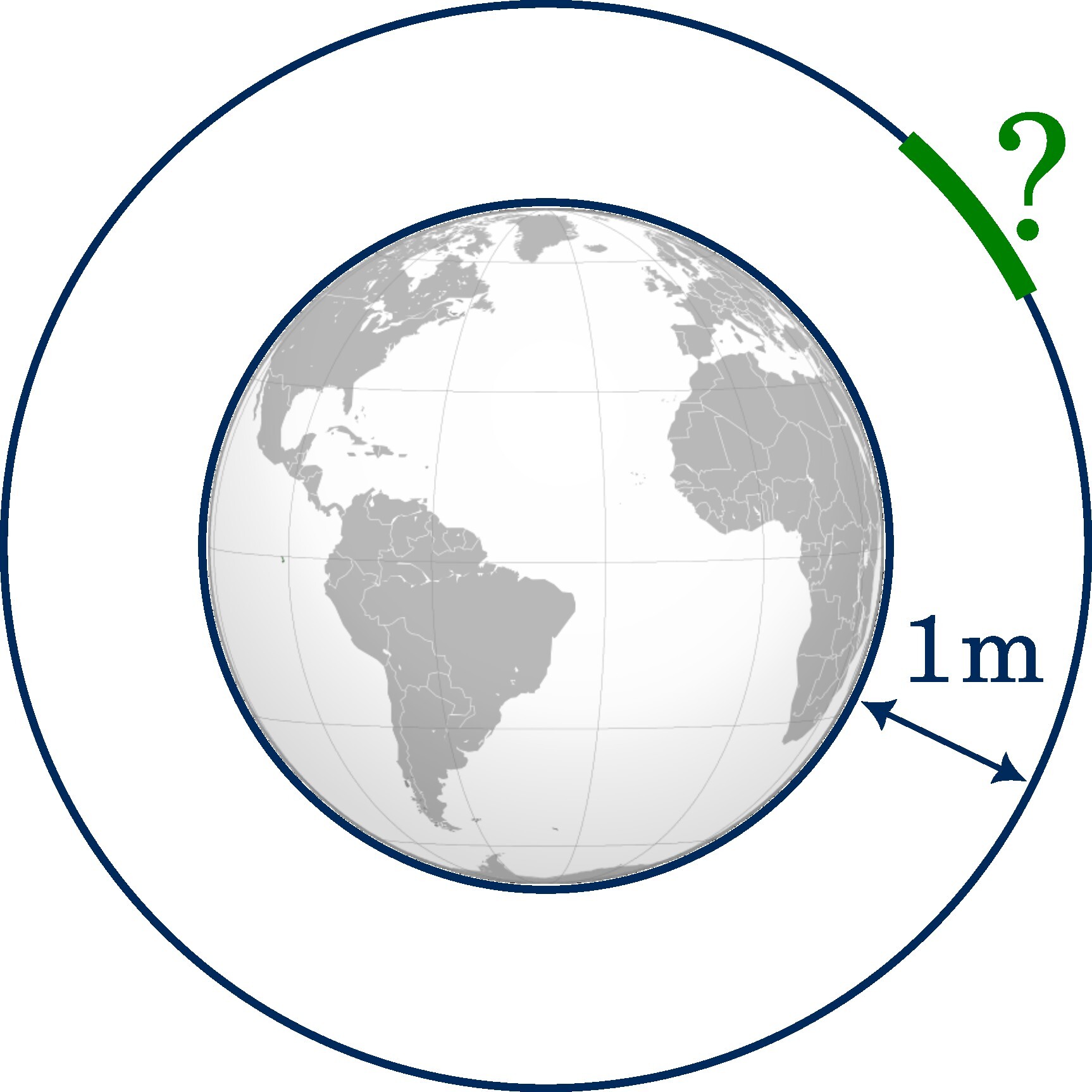
Although students get often bored during my derivation and explanation, they are usually left surprised when they see the bizarre and counterintuitive solution. As the string must be raised all along the entire 40,000 km (25,000 mi) circumference, one might expect several kilometres of additional string. Surprisingly, the answer is $2\pi$ or around 6.3 metres (21 ft). This quiz challenges our intuition even more if we state the question differently. For instance, what is the height above the surface if a string is tied around the Earth’s equator and then an additional bit of string is added?

"But how does this answer my question?" is the usual reaction after the initial joy has worn off.

How this relates to tendon displacement

Now, let’s enter the follow-up thought experiment: A tendon-driven continuum robot of length $L$ is bent by an applied tendon displacement $\Delta L$ to form a full circle.

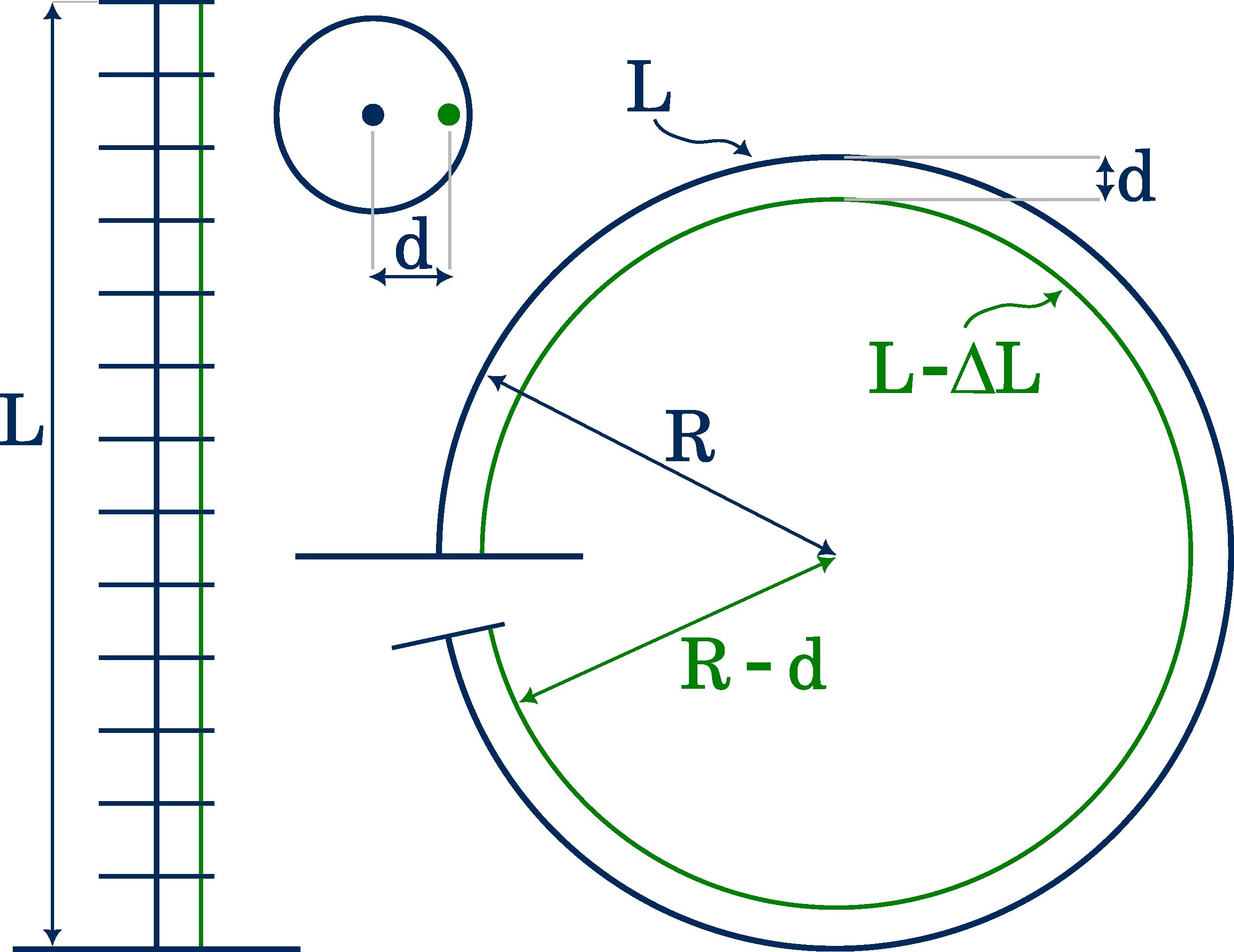
From the right image, we can derive two equations:

\[\begin{aligned} U_\text{outer} &= L = 2\pi R\\ U_\text{inner} &= L - \Delta L = 2\pi \left(R - d\right) \end{aligned}\]

The first equation describes the circumference of the outer circle being the backbone of the continuum robot. The second one reflects the circumference of the inner circle being the initial tendon length, $L$, minus the tendon displacement, $\Delta L$. Here, I assume that infinitely many infinitesimal thin spacer disks guide the tendon into a circular path, i.e. a fully constrained tendon path¹, where the tendons follow a continuous curve parallel to the backbone. Also, our assumptions are necessary for the constant curvature kinematics framework to work.

Coming back to the equations, by computing the differences, we get that the required tendon displacement is

\[\begin{aligned} \Delta L &= 2\pi d, \end{aligned}\]

where $d$ is the distance of the tendon routing hole to the backbone. This answer may be surprising because the tendon displacement only dependents on the parameter $d$, which is relatively small compared to the length of the manipulator, $L$.

In conclusion, a tendon displacement range $\Delta L \in [-6d,6d]$ is probably enough as we typically do not require TDCR segmentsto bend into full circles (or more).

Yet, another surprise

The string girdling Earth puzzle essentially leads to answer to the tendon displacement question. Another surprising aspect is: If the Earth’s cross-section is a convex area, then the string needs to be lengthened by $2\pi$ meter to raise the rope one meter above its surface. This holds true regardless of how many sides the convex area has. A derivation can be found in The Math Images Project.

Exploiting this neat aspect, we can relax the condition related to constant curvature on our tendon routing path, such that the area encompassed by the tendon just needs to create a convex area. Therefore, partially constrained tendon paths¹ and non-constant curvature shapes can be considered as well. And, the range of tendon displacement remains the same, which means that our equation is still valid as long as the encompassed area is convex.

A surprising connection, don’t you think?

References

1. P. Rao, Q. Peyron, S. Lilge, J. Burgner-Kahrs: How to Model TendonDriven Continuum Robots and Benchmark Modelling Performance. Frontiers in Robotics and AI, vol. 7, p. 223, 2021. doi: 10.3389/frobt.2020.630245 ↩ ↩²