


Next: November 20
Up: November 15
Previous: November 15
Matrix chains
Suppose you (or your computer) have to multiply a chain of matrices:
Matrix multiplication of a pair of matrices is well-defined (if it's
defined at all), and for more than two, multiplication is associative:
You get the same answer, either way, but the amount of work (measured
in the number of multiplications) may well differ. Suppose 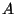 is a
is a
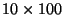 matrix,
matrix, 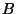 is a
is a
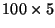 matrix, and
matrix, and 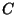 is a
is a
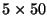 matrix. If we group the multiplication as
matrix. If we group the multiplication as 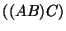 ,
then the amount of work is proportional to
,
then the amount of work is proportional to
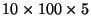 +
+
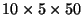 , or 7500 multiplications. On the other hand, if
we grouped the product as
, or 7500 multiplications. On the other hand, if
we grouped the product as 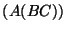 we'd be faced with
we'd be faced with
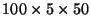 +
+
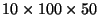 , or 75000 multiplications -- 10
times as many! So, order counts.
, or 75000 multiplications -- 10
times as many! So, order counts.
How much work is it to check out all the ways of parenthesizing a
product? Try it out with just a few matrices (no more than 10), and
you'll find the number of groupings grows rapidly -- it's
proportional to 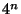 for
for 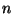 matrices. The exact number of groupings
is a challenging thing to calculate, it's called the Catalan number.
matrices. The exact number of groupings
is a challenging thing to calculate, it's called the Catalan number.
It's not practical to check something proportional to 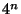 before we
even get down to the business of calculating the matrix product.
Let's look at the structure of the problem. Suppose we (magically)
have an optimal grouping for multiplying
before we
even get down to the business of calculating the matrix product.
Let's look at the structure of the problem. Suppose we (magically)
have an optimal grouping for multiplying 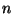 matrices. Examine the
last matrix multiplication performed:
matrices. Examine the
last matrix multiplication performed:
If the entire product is optimal (uses the fewest possible
multiplications), then the subproducts
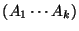 and
and
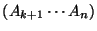 must also be optimal. Otherwise, if there were a better
way to calculate either subproduct, it would lead to a more efficient
grouping to calculate the entire product. So, our Dynamic Programming
solution will keep track of the best ways of calculating subproducts,
and combine these into the best ways of calculating the entire
product. We can define the following array, for
must also be optimal. Otherwise, if there were a better
way to calculate either subproduct, it would lead to a more efficient
grouping to calculate the entire product. So, our Dynamic Programming
solution will keep track of the best ways of calculating subproducts,
and combine these into the best ways of calculating the entire
product. We can define the following array, for
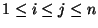 :
:
![$\displaystyle C[i][j] =$](img281.gif)
minimum cost of multiplying
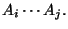
Clearly ![$ C[i][i]$](img283.gif) is zero, for all
is zero, for all 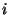 , since there is no cost in the
``product'' of one matrix. If
, since there is no cost in the
``product'' of one matrix. If 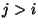 , then we get the recurrence
relation:
...where
, then we get the recurrence
relation:
...where
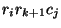 is the product of the number of rows in
matrix
is the product of the number of rows in
matrix 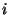 , the number of rows in matrix
, the number of rows in matrix 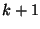 , and the number of
columns in matrix
, and the number of
columns in matrix 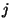 .
.



Next: November 20
Up: November 15
Previous: November 15
Danny Heap
2002-12-16
![]() for
for ![]() matrices. The exact number of groupings
is a challenging thing to calculate, it's called the Catalan number.
matrices. The exact number of groupings
is a challenging thing to calculate, it's called the Catalan number.
![]() before we
even get down to the business of calculating the matrix product.
Let's look at the structure of the problem. Suppose we (magically)
have an optimal grouping for multiplying
before we
even get down to the business of calculating the matrix product.
Let's look at the structure of the problem. Suppose we (magically)
have an optimal grouping for multiplying ![]() matrices. Examine the
last matrix multiplication performed:
matrices. Examine the
last matrix multiplication performed: