Dynamic Programming

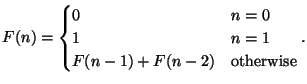
You've already seen problems that can be reduced to subproblems with the same structure -- recursion comes to mind. A classical sequence whose value is expressed recursively is the Fibonacci sequence:

$$F(n) = \begin{cases} 0 & n = 0\\ 1 & n = 1 \\ F(n-1) + F(n-2) & \text{otherwise} \end{cases}.$$

Given this recursive definition (a recurrence relation), it is very efficient in programmer labour to write down an algorithm:

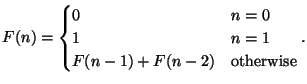
int fib(int n)
{
    if (n < 2) {
        return n;
    } else {
        return fib(n-1) + fib(n-2);
    }
}

However, for fairly modest $n$ this algorithm turns out to be inefficient for the computer. Consider fib(8): fib(7) gets called once, fib(6) gets called twice, ...the complexity ends up being exponential.

A more reasonable way to calculate fib(n) is from the bottom up:

int fib(int n)
{
    int *f, answer;
    if (n < 2)
        return n;
    f = new int[n+1];
    f[0] = 0;
    f[1] = 1;
    for (int i = 2; i <= n; i++)
        f[i] = f[i-1] + f[i-2];
    answer = f[n];
    delete f;
    return answer;
}

Even given the new/free operations to allocate and free memory, this is a much better algorithm, being $O(n)$. It is also an example of Dynamic Programming.

Another algorithm that fits the same mold is the Floyd-Warshall all-pairs shortest distance. At the heart of that algorithm was the following recurrence:

$$D[i,j,k] = \min \{D[i,j,k-1], D[i,k,k-1] + D[k,j,k-1]\}.$$

If you were to use recursion to solve this problem, you'd need two recursive calls to evaluate the minimum. Each of those would require two recursive calls ... and you'd have exponential complexity.

The Dynamic Programming approach would be to start at the bottom: $D[i,j,-1]$ is defined to be the weight of edge $(i,j)$, and we can easily build up a three-dimensional array starting from these values, and using the recurrence. The solution presented in our course readings uses a two-dimensional array (saving space), although the algorithm is still $O(n^3)$.

What are the principles that tie these approaches together under the heading Dynamic Programming? Given a problem that you want to find an optimal solution for:

1. Characterize the optimal subproblem structure.
2. Define an array (table) that contains the value you want to optimize for, plus all the relevant subproblems.
3. Write down a recursive definition for building the array.
4. Compute the solution from known values.