


Next: October 11
Up: October 9
Previous: But first, structs and
Graph definitions
The intuitive notion of a graph is a drawing of (possibly labeled)
nodes (often circles) with edges connecting some of them. Graphs turn
out to be a model that many problems can be translated to, and often
solved. You've already seen a special case of a graph, since a tree
is an acyclic, connected graph with one node distinguished as the root
(see definitions below).
Here are some formal definitions:
- A graph (denoted
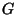 ) is a pair of sets
) is a pair of sets 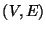 , where
, where 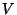 is the
set of vertices (or nodes) and
is the
set of vertices (or nodes) and 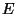 is the set of edges. Vertices
are usually the elements of the problem we're interested in. Each
edge connects two vertices, so it can be represented as a pair
is the set of edges. Vertices
are usually the elements of the problem we're interested in. Each
edge connects two vertices, so it can be represented as a pair
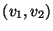 .
.
- We can also denote the vertices of a graph
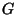 as
as 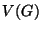 and its
edges as
and its
edges as 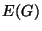 . The number of vertices,
. The number of vertices, 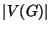 is the called
is the called
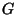 's order, and the number of edges,
's order, and the number of edges, 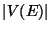 is called
is called
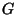 's size.
's size.
- Since edges are ordered pairs,
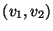 indicates there is
an edge from
indicates there is
an edge from 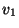 to
to 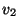 , but not necessarily from
, but not necessarily from 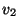 to
to 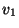 -- if so there must be an edge
-- if so there must be an edge
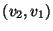 in
in 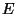 . When this
distinction is important, we have a directed graph. In this course
the edge relationship is usually symmetrical: there is an edge
. When this
distinction is important, we have a directed graph. In this course
the edge relationship is usually symmetrical: there is an edge
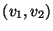 if and only if there is an edge
if and only if there is an edge
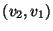 . In this case the edge
is in fact the set
. In this case the edge
is in fact the set
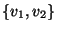 (since sets have no order), and we
have an undirected graph. A vertex may not have an edge to
itself (unless we have a pseudograph).
(since sets have no order), and we
have an undirected graph. A vertex may not have an edge to
itself (unless we have a pseudograph).
- When two vertices share an edge they are ``adjacent'' (or
``neighbours''). The number of neighbours vertex
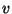 has is called
the degree of
has is called
the degree of 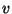 (for a directed graph we have in-degree and
out-degree). A path is a list of vertices where each pair of
vertices that are adjacent in the list are also adjacent in the graph.
(for a directed graph we have in-degree and
out-degree). A path is a list of vertices where each pair of
vertices that are adjacent in the list are also adjacent in the graph.
- A circuit is a path that begins and ends on the same
vertex without repeating any edges. A cycle is a path that
begins and ends on the same vertex and doesn't repeat any vertices
(and usually includes at least three vertices).
- Vertices
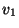 and
and 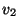 are connected if there is a
path beginning with
are connected if there is a
path beginning with 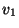 and ending with
and ending with 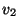 . Graph
. Graph 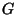 is
connected if every pair of vertices in
is
connected if every pair of vertices in 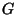 is connected.
is connected.
- Graph
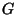 is complete if every vertex is a neighbour of every
other vertex. Clearly a complete graph is also connected. If
is complete if every vertex is a neighbour of every
other vertex. Clearly a complete graph is also connected. If 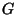 is a complete, undirected graph, how many edges does it have? It
turns out that two complete graphs of the same order (same number of
vertices) are equivalent (isomorphic, which is defined later), so it
makes sense to talk about the complete graph of order 2,
is a complete, undirected graph, how many edges does it have? It
turns out that two complete graphs of the same order (same number of
vertices) are equivalent (isomorphic, which is defined later), so it
makes sense to talk about the complete graph of order 2,
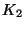 , or order 4,
, or order 4, 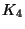 , etc.
, etc.
- A colouring is an assignment of colours to a graph so that
- every vertex is assigned a colour.
- no two neighbouring vertices are assigned the same colour
Usually we represent the colours by small integers. If it is
possible to colour a graph with 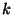 colours, we say the graph is ``
colours, we say the graph is ``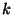 colourable.'' If you know that it's possible with colour a graph
with
colourable.'' If you know that it's possible with colour a graph
with 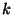 different colours, then you can certainly colour it with
more than
different colours, then you can certainly colour it with
more than 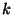 colours: being
colours: being 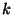 colourable doesn't require that all
colourable doesn't require that all
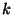 colours are used, only that
colours are used, only that 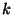 colours are enough.
colours are enough.
- The chromatic number of graph
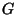 , denoted
, denoted 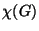 , (that's
the greek letter chi) is the minimum number of
colours required to colour
, (that's
the greek letter chi) is the minimum number of
colours required to colour 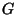 . It's easy to come up with an upper
bound for
. It's easy to come up with an upper
bound for 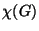 , since you
, since you 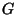 is certainly
is certainly 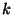 colourable if
colourable if
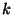
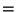
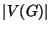 . Usually
. Usually 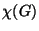 is less than
is less than 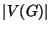 , but in
the case of a complete graph
, but in
the case of a complete graph 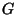 ,
, 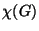
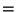
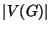 .
.
- To prove that
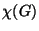
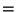
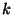 for a given graph
for a given graph 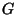 , you need
to prove both that
, you need
to prove both that 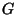 is not
is not 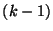 colourable, and that
colourable, and that
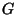 is
is 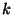 colourable.
colourable.



Next: October 11
Up: October 9
Previous: But first, structs and
Danny Heap
2002-12-16