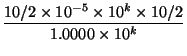Even if your computer had no other source of error in calculating
![]() , it would need to fit it into some finite memory location. In
what follows we'll assume (to make our calculations easier) that our
computer represents floating point numbers using scientific notation
and 5 decimal (base 10 digits). So, for example,
, it would need to fit it into some finite memory location. In
what follows we'll assume (to make our calculations easier) that our
computer represents floating point numbers using scientific notation
and 5 decimal (base 10 digits). So, for example,
![]() would be represented as:
would be represented as:
The decimal (aka base 10) expansion of ![]() is
2.718281828459045...If we insist on squashing it into 5 digits, we
have two reasonable choices: 2.1782 (truncation) or 2.1783 (rounding).
Truncation is computationally easier, since for rounding we must
examine the first omitted digit and round up if it is 5 or greater,
down otherwise. How bad are our 5-digit approximations? A reasonable
measure would be to find the difference between our approximation and
the true value, and see what proportion of the true value the
discrepancy is. This is called the relative error:
is
2.718281828459045...If we insist on squashing it into 5 digits, we
have two reasonable choices: 2.1782 (truncation) or 2.1783 (rounding).
Truncation is computationally easier, since for rounding we must
examine the first omitted digit and round up if it is 5 or greater,
down otherwise. How bad are our 5-digit approximations? A reasonable
measure would be to find the difference between our approximation and
the true value, and see what proportion of the true value the
discrepancy is. This is called the relative error:
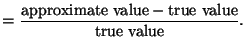
So, what's the worst relative error we can expect from rounding?
Well, if the first digit that we omit is a 5 followed by zeros, we
round up and our total error is half the distance between two
consecutive numbers. For example, if the true value were 5.43215, to
keep only 5 digits we'd round up to 5.4322, and our total error would
be 0.00005. Notice that the total error changes if we approximate
5.43215 ![]()
![]() by 5.4322
by 5.4322 ![]()
![]() (the total error
gets a thousand times bigger). What we really want is the relative
error.
(the total error
gets a thousand times bigger). What we really want is the relative
error.
Re-write 5 as 10/2, since what's important is that 5 is half of the
base (10). Also, since we're trying to find the maximum relative
error, make the denominator as small as possible by having mantissa
1.0000. Then, no matter what exponent ![]() you raise 10 to, the
relative error is:
you raise 10 to, the
relative error is: