The Job Shop Problem
In this problem, we need to schedule tasks on different work stations, with some constraints. The tasks are part of a job - say building a bike. - each task in a job must start only after the previous task has been completed. - a task cannot be paused - the time it takes to complete cannot be divided. - the work stations can only work on one task. You can have a look here for a more complete - and graphical - explanation.
3 job shop
In this tutorial we will study the following problem. We have three different jobs, each one consisting of three different tasks. Each task is assigned to a machine and has a predefined duration. We have three jobs jo0, job1, job2 containing task. We define the problem parameters in the following lists, where each element of the list is a pair (m,d) where m represents the machine where the task has to be executed and d is the duration of the task:
The jobs are a list of tasks, and each task is a pair where the first element represents the machine number that can execute the task and the second is the duration of the task.
Encoding the problem
Now we have a problem where atoms - the tasks - have different durations. We cannot encode it as a boolean formula as in the 4-queens problem, we will need numbers and related operators to express the problem ...
Theory of linear integer arithmetic
TODO
Back to the problem
Each task has two parameters: - the job it is part of. - the duration of the task. And there is one unkown - the start time of the task on the machine. We still want to encode the problem as a propositional formula, but now each formula uses linear integer arithmetic.
3 jobs shop
Now let us clearly define the problem. We need to declare the variables we need, here representing the starting times of the task:
A first constraint we need to add is that all starting times for the tasks are positive:
We can first express the "all tasks in a job should be executed sequentially" constraints. In each job, the start time of a task should be greater than or equal to the start time of the previous task plus the duration of this task. This gives a conjunction of comparisons for each job:
Then we need to add the "a machine can execute only one task at a time" constraints. One way to do this is to think about it this way: the machine executes only one task at a time if and only if all the tasks executed on the machine do not overlap. When looking at the sequence of the tasks executed on a particular machine, each task starts at least after the previous has finished. And this has to be true for every possible sequence of tasks. For each machine, we need to enumerate the possible sequence of tasks (we have a disjunction here) and then constrain this sequence (a conjunction). This is something that a programmer would want to automatize, but have a look a the final solution for this problem:
Try to check if it is satisifiable using z3 here. Here is the solution I got:
So if we represent it on a diagram where each job has a color, each line represents a machine and the tasks are the blocks:

This doesn't seem very optimal, and the machines are idle most of the time. We expressed all our constraints and the solver returns a correct answer but not the optimal one. However, z3 can help us!
3 job shop: optimal scheduling
Some SMT solvers can additionally solve max- or min- sat problems, meaning that they can find a model that satisfies a formula minimizing of maximizing another constraint. z3 supports the following constructs: (minimize ...) (maximize ...) You have to place them before the (check-sat) construct, and z3 will handle the optimization problem.
Back to our problem
In the solution above, the overall completion of all the jobs takes too much time. One way of optmizing that is to look for the solution that completes the earliest. We want to minimize the maximum of all the finish times of the jobs:
Remark: we have to specify the definition of the max function here.
I got this solution:
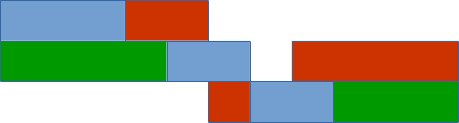
That's much better!