Player’s Guide
A New Guide to the Starting Hands
in Texas Hold’em Poker.
The key decision any hold’em player makes is
whether or not to play the starting 2 card hand they are dealt. And, if so, how
to play it.
We present here some valuable new facts.
.
Our Model
We have developed these new facts from a new,
very comprehensive, computer simulation of our own design.
Simulate? Smiluate!
This document is a Player’s guide. It’s meant to bring the practical
implcations of our results to bear. To be helpful to the hold’em player who may
or may not care about simulation.
If you’re a poker player who is also a technical
person, or if you’re just curious what a sophisticated simulation program looks
like inside, then we invite you to ask about getting the complete source code
of this program as well as the detailed print outs from a rreasonable run.
For information about how to secure the source
code and detailed print outs, see our web page at: http://www.evgr.com/poker,
or write to us by e-mail or snail-mail at the address(es) on the cover.
This source code constitute the proofs as to the
facts we do summarize here. Usually the best you can get from a poker book is
the author’s naked recommendations. No proof, no detailed calculation
worksheets and certainly no source code.
Shuffle and Deal
First, imagine a simple computer program that
shuffles a regular deck of 52 cards and deals out hands to 10 players, plus 5
community cards face up on the board.

The “shuffle” involves picking these 25 cards at
random (without replacement) from the deck of 52
“Dealing” is done simply by assigning beforehand
particular sequence numbers to particular parts of a complete round of play.
the 7th card picked, for example, is always the 1st card
dealt to player 7, and so on.
![]() Randomized
shuffling and dealing should be part of any poker simulation. The only thing
unusual in what we have done is to have read about, and worried a greal deal
over, the quality (and efficiency) of the random number generator algorithm we
would use. For more details on that, check out random.zip in the
FREEWARE section of our website (http://www.evgr.com/poker).
Randomized
shuffling and dealing should be part of any poker simulation. The only thing
unusual in what we have done is to have read about, and worried a greal deal
over, the quality (and efficiency) of the random number generator algorithm we
would use. For more details on that, check out random.zip in the
FREEWARE section of our website (http://www.evgr.com/poker).
Hero’s Play
Player 1 is always our hero. Whatever starting
hand our hero is dealt becomes the focus hand in that round of play. Focus
hands are always played aggressively all the way to the river.
To illustrate this, suppose Player 1 gets dealt
a pair of 5’s. During that round all of the other players make four
decisions: (a) to play or fold before
the flop, (b) play or fold after the flop,(c) play or fold after the turn and
(d) play or fold after the river card is turned up.
At the showdown it may be that everyone but our
hero has folded. Fine, then 55’s frequency counter for 0 river foes gets bumped
by 1. And 55’s win counter for 0 foes at the river also gets bumped by a
fraction, depending at what stage of play the last foe in the round folded.
Depending on the HE Table environment, there
will usually be one or more foes contesting the river. If it turns out that our
hero has a winning-ranked hand along with one or more foes, then this tie is
divided up proprtionately. Let’s say hero ties with 2 foes, then hero’s
frequency counter for 2 foes gets bumped by 1 and his win counter for 2 foes
gest bumpted by 0.3333.
So, we continue in this way for several million
(or billion) rounds of play, keeping track of the frequencies and wins for each
condition being examined in the simulation. When the run is done, our program
then goes through and calculates, for each condition, the liklihood of winning,
or p(win) and saves that information as well.
Foes
Foes are always players 2,3,4,5,6,7,8,9 and up
to 10, depending on the particular condition. the foes our hero faces sit at 5
different HE Tables in the same round. Don’t try this in a poker room. It only
works on a computer.
HE Tables 1, 2, 3 and 4 always have 10 players.
At HE Table 1 they play as tight as you’ll
likely ever find. Every foe assumes that there will only, on average, be 2.5
other players seeing the flop. He/she plays rationally, based on an expert
knowledge of “old” facts.[1]
In this case he/she would play the hand he/she was dealt only with knowledge
that it had favorable odds of winning at a HE Table with 3.5 players (since
he/she will always see our hero’s bet).
If the foe was player 8 or 9, however, he/she
would have additional information. there would be the cumulative prior action
of all preceding players (our hero and other foes) to use as well as an
expectation about overall HE Table conditions.
HE Tables 2, 3 and 4 are similar to HE Table 1
except they are progressively “looser” in pre-flop play.
the idea of “looseness” is not vague in this
simulation model. It, and how the foes play, consist exactly of the following
rules strictly enforced (as only a computer can do).
ü
At HE Table 1 if a player does not have
any current information, that is no other player has acted yet, a foe will
always assume at least 2.5 small bets have been (or will be) put into the pot,
as we just described above. At HE Table 2 the assumption is 3.5. HE Table 3
believes in 4.5 and HE Table 4 foes assume 5.5.
ü
This starting assumption gets modified by
actual play. For example, Player 5 always gets to adjust his/her overall
assumption about the Table if Players 2, 3 and 4 all are in the pot ahead of
him/her.
ü
the foe uses this “assumption” to
calculate the odds the theoretical pot is offering for the particular starting
hand he/she has just been dealt. This is expert play based on “old” facts.[2]
ü
Armed with (a) the odds of winning at the
river against the presumed number of foes for this HE Table, adjusted by the
actual number, in case that is greater by the time this foe must make a
play/fold decision, and with (b) the odds the presumed pot is offering to
continue playing, the foe makes a rational decision whether in fact to play or
fold before the flop.
ü
After the flop, the foes at these HE
Tables will then play only when they have either a made hand or a 1 card draw
to a straight or a flush. At the river, they will play only when they’ve made
at least a pair or better. Missed straight and flush draws fold at that point.
At HE Table 5 the players are as loose as
possible. they play the classic showdown game where every player goes to the
river. Except we provide here for 2 player showdowns (consisting of thero plus
Player 2), 3 player showdowns (add Player 3) and so on up to a 10-player
showdown (add Players 4 thru 10).
So, HE Table 5 is really 9 different HE Tables, each with a different number of starting
players. But instead of numbering them as such we preferred to simply indicate
the number of players at the river as being 3, for a 3-player showdown game, 5
for a 5-player game, and so on. That way, we can easily compare them with
number of players at the showdown under the more realistic playing conditions
of HE Tables 1, 2, 3 and 4.
If you wish, you can imagine in our study that
Hero is sitting simultaneously at 5+8=13 different HE Tables, four of them
where the foes play their hands quasi-realistically and nine of them where all
of the foes play loose and crazy, but at eight of these they are playing
short-handed.
Playing Position
Although playing position is generally thought
to be the most important factor in selection of starting hands in hold’em, it
is not particularly important to the conclusions we’ve drawn here.
We keep track of the fate of starting hands
under the control of our hero. All other hands are distributed randomly across
position. Our hero is always, in effect, acting “under the gun” but could care
less.
If you wish to vary your starting hand selection
based on your playing position, which is fundamental to the playing strategies
advocated by noted poker authors, then you’ll be using the overall ranking of
each hand as a basis for doing so anyway.
That’s it! Or, at
least, that’s the beginning of our more detailed story.
Look at it this way. We’ve covered in our model
a broad spectrum of HE Table conditions varying from very tight to maximally
loose. We’ve also covered the issue of number of players in both possible ways:
the number of players at the HE Table in the first place, and the number of
good players out of 10 who play rationally and by doing so end up as foes at
the river.
This simulation is, we believe, unique
Aggression
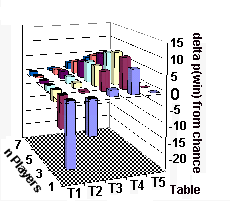 Since our hero always plays aggressively, we need
to be able to separate out the wins that occur because of the absolute winning
power of the hand from those that occur because the winning hand folded before
the showdown, at least for HE Tables 1, 2, 3 and 4. The proportion of p(win)
that is left represents the pure power of the hand.
Since our hero always plays aggressively, we need
to be able to separate out the wins that occur because of the absolute winning
power of the hand from those that occur because the winning hand folded before
the showdown, at least for HE Tables 1, 2, 3 and 4. The proportion of p(win)
that is left represents the pure power of the hand.
 The
first step is to find out how much of the total p(win) is due to the winning
hand having folded before the showdown. This is shown in Figure ___ as
fluctuations above and below the zero plane..
The
first step is to find out how much of the total p(win) is due to the winning
hand having folded before the showdown. This is shown in Figure ___ as
fluctuations above and below the zero plane..
This is easy in the case of HE Table 5, because
every foe is playing aggressively as well. Figure __ shows the difference
between chance p(win), for each condition in our model, and actual p(win)
accumulated across all 169 starting hands. the zero plane is chance, and you
will be able to see that regardless of the number of players in the game, in
this case, there is no difference between chance and actual p(win)s for HE
Table 5.
Any fluctuation above or below the zero plane in
the Figure reflects cases where a random hand played aggressively either picks
up wins from hands that could have won if they had not folded (above zero), or
loses wins because the hand was played too aggressively. That is, our hero
should have folded sometimes (below zero).
Somewhere between the HE Table 2 and HE Table 3
overall playing conditions aggression acquires value, at least against a small
number of foes.
At some tighter playing conditions aggression with
a random starting hand is a losing strategy. At some looser playing conditions
aggression with a random hand has positive value.
Since the only difference in the foe’s decision
rules between HE Tables is on whether or not to play before the flop, we can
see that when everyone at the Table believes there will be an average of about
5 players seeing the flop, or so, selective aggression can become an important
factor in play. This increase in overall expectation can be dramatic,
especially when only 1 or 2 foes survive to the river.
Figure 1 also shows as the number of foes who
play to a showdown increases, when each has an opportunity to fold, the less
value there is in aggression with a random starting hand. In other words, the
more likely you are to be beat.
Power
So, by subtracting from the measured p(win)s in
our simulation run the effect of aggression, we are left with an estimate of
the pure playing power of each of the 169 starting hands in Texas hold’em.
We turn now to see how well some of the
conventional authorities and writers have done in the past when attempting to
derive this estimate of power .. using private methods never fully revealed,
even if you buy their book(s).
We sill examine in detail the recommendations
about startintg hold’em hands in each of the following poker classics,
ü Hold’em
Poker by David Sklansky and Mason Malmuth
ü Winning
Low Limit Hold’em by Lee Jones
ü “Super/System’s Power Poker Course in
Limit Hold’em” by Bobby “The
Owl” Baldwin, in Super/System by Doyle “Texas Dolly” Brunson.
Sklansky Groups
Sklansky was the first poker author to have both
ranked all of the starting 2-card hands, and then grouped them with
recommendations about how to play each group.
David “Einstein”
Sklansky (a nickname attributed to him in Doyle Brunson’s book, Super/System)
has been a professional poker player and poker theoretician for decades, and
his advice is widely respected.
As for the starting hold’em hands, did he get it
right?
The Sweet 16.
Let’s start off with the good ones. The top 16
ranked starting 2-card Hold’em hands are fundamental to solid play. They
constitute only about 7% of all hands you will be dealt, however, so it’s
improbably that you will get rich by limiting your play to just these.
But it is imperative for good play that you KNOW
what they are, and how well they stack up against each other.
Table 1 - Sklansky's Group 1 hands
|
AA |
KK |
QQ |
JJ |
AKs |
Sklansky (actually
Sklansky and Malmuth, which we will shorten to S&M to save space here)
defined 5 members of Group 1, as shown in Table ___above. They also indicate in
their book that the overall rank order
of these hands is as shown reading from left to right. AA, that is, is the
highest ranking hand of all.

We confirmed, as shown in Figure __, that these
are, indeed, the 5 best starting 2-card hands as well as that their actual
ranks within the group are exactly as S&M represent.
![]() AA
and KK are substantially more powerful than lower ranking hands, however, even
than QQ. These two hands are also the only ones with positive power ratings at
HE Table 1.
AA
and KK are substantially more powerful than lower ranking hands, however, even
than QQ. These two hands are also the only ones with positive power ratings at
HE Table 1.
You will recall this was the “tightest” HE Table
in our study. Under very tight HE Table conditions these are the only starting
hands that should be raised for value. But, as we shall see, if you find
yourself at a very tight HE Table you should probably get up and go find better
playing conditions anyway.
Table 2 - Sklansky's Group 2 hands
|
TT |
AQs |
AJs |
KQs |
AK |
The S&M Group 2
hands are shown above.
Since S&M indicate that their determination
of relative rank order within the group is “approximately” as shown, from left
to right., we need to point out a minor correction before otherwise endorsing
the membeship of Group 2.
The overall power of AK is slightly greater than
that of KQs, so we would reverse the order of these two hands within the Group.

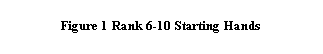 We
confirm that the membership of Group 2 is the same as that asserted by S&M.
Or, rather, we confirm that these hands rank 6, 7, 8, 9 and 10 in overall
playing power. However, there is actually a small advantage held by AK over
KQs, so our list (Figure ___) shows a correction in the relative rank order
within the group, which is just a matter of fine detail.
We
confirm that the membership of Group 2 is the same as that asserted by S&M.
Or, rather, we confirm that these hands rank 6, 7, 8, 9 and 10 in overall
playing power. However, there is actually a small advantage held by AK over
KQs, so our list (Figure ___) shows a correction in the relative rank order
within the group, which is just a matter of fine detail.
.Why Raise?
There are 10 hands in
these groups, but they are not treated equivalently for purposes of decisions
to raise (or not).
Although the S&M
rationale for doing so certainly appears to be plausible enough, they do not
present any computational rationale or other proof. One must take some of it on
faith. As it turns out, however, there have probably been some errors made in
these recommendations.
S&M give different
reasons for raising (or not), including each of the following.
ü raise
4 (AA, KK, QQ, AK) in part because “..they lose much of their value in large
multi-way pots.”
ü raise
4 (Aks, Aqs, AJs and KQs) only sometimes in part because “..they do play well in multi-way pots.”
ü raise
1 (JJ) in a tight game ”..to get out
hands like A9.” the idea being that this hand also loses value in multi-way
pots, or perhaps that it has less value at a loose HE Table .. which is a
similar, but not identical idea.
ü Never
raise1 (TT) for reasons that are not stated.
These are key ideas in
current hold’em playing strategy. Since S&M assume certain difficult to
prove facts that our model encompasses, however, we can put these assumptions
to test.
We measure directly the effect of multi-way
action. Also, we vary the degree of looseness of the Table in seeing the flop.
So, we can separate out the effects of HE Table conditions and number of foes
contesting the pot for each starting hold’em hand.
When we look at these facts for the 10 best
starting hands, we get the results shown in Table ___ (below).
.
Table 3 - MAD[3] Sensitivity to Playing Conditions
|
Rank |
Hand |
Table |
nFoes |
T x F |
|
1 |
AA |
0.0 |
0.0 |
0.0 |
|
2 |
KK |
0.1 |
0.0 |
0.1 |
|
3 |
QQ |
2.3 |
1.9 |
2.5 |
|
4 |
JJ |
5.7 |
4.6 |
6.6 |
|
5 |
AKs |
6.1 |
5.3 |
7.2 |
|
6 |
TT |
7.1 |
3.7 |
7.2 |
|
7 |
AQs |
5.3 |
5.4 |
8.9 |
|
8 |
AJs |
9.7 |
9.0 |
13.1 |
|
9 |
AK |
13.3 |
20.6 |
27.9 |
|
10 |
KQs |
5.7 |
4.2 |
8.4 |
The mean absolute
deviation[4]
(MAD) in the rank of a hand among all starting hands is a measure of
sensitivity by the hand to playing conditions. Table ___shows MADs for
variations in HE Table conditions, variations in number of quasi-realistic foes
contesting the pot at the river and in combinations (or interactions) of these
two conditions.
Of the 4 hands S&M assume would be most
sensitive to multi-way action (AA, KK, QQ, AK) only one (AK) actually is. In
fact, it’s mean absolute deviation in rank (among all 169 possible hands) due
to varying numbers of foes at the river, at 20.6, makes it one of the most sensitive of hands.
By contrast, the very least sensitive hands to multi-way action are AA, KK and QQ.
Of the 4 hands S&M assume “play well” in
multi-way pots (AKs, AQs, AJs and KQs), this conclusion can only be correct if
by playing well what is meant is that in each case the hand ranks at about the
median of all 169 possible hands in sensitivity to multi-way action.
These hands that are presumed to “play well” in
multi-way pots do NOT increase in relative value with increasing multi-way
action at all, as many current poker players are inclined to believe.
S&M ignore TT and reserve a special status
for JJ in terms of multi-way action. Yet, neither of these hands seem
particularly sensitive to multi-way action and it is difficult therefore to
take those recommendations too seriously.
Table 4 - Mean Rank Order of Hands
|
Number of Players at River |
||||||
|
Rank |
|
2 |
3 |
4 |
5 |
6 |
|
1 |
AA |
1.0 |
1.0 |
1.0 |
1.0 |
1.0 |
|
2 |
KK |
2.0 |
2.0 |
2.0 |
2.0 |
2.0 |
|
3 |
QQ |
3.0 |
3.0 |
3.0 |
3.0 |
3.0 |
|
4 |
JJ |
14.4 |
4.8 |
4.4 |
4.3 |
4.0 |
|
5 |
AKs |
5.0 |
5.4 |
5.4 |
7.2 |
26.6 |
|
6 |
TT |
26.4 |
11.0 |
8.0 |
6.0 |
5.8 |
|
7 |
AQs |
9.2 |
8.6 |
8.6 |
11.8 |
33.0 |
|
8 |
AJs |
9.2 |
8.6 |
8.6 |
11.8 |
33.0 |
|
9 |
AK |
7.5 |
7.8 |
10.0 |
26.2 |
40.0 |
|
10 |
KQs |
11.2 |
12.2 |
18.2 |
18.0 |
20.0 |
Another way to look at these assumptions is to
show the mean rank order of each hand for 2, 3, 4, 5 or 6 foes at the river, as
shown in Table ___ (above).
S&M ignore TT, but it actually benefits from
multi-way action, as does JJ. We would therefore urge you to consider raising
these hands for value if the raise is not likely to drive out foes in a loose
game
Five of these hands are particularly vulnerable
to heavy multi-way action, the kind that increases the liklihood of 6 or more
foes playing to a showdown (Aks, AQs, AJs, KQs and AK). With moderately loose
showdown action they are neither especially sensitive, one way or the other.
One hand, AK, suffers tremendously with nearly
every additional foe who plays to a showdown. This is the only hand in the
group that should be raised pre-emptively in an effort to weed out the
competition.
With these changes, then, we would recommend a
re-write of the pre-flop raising recommendations for Sklansky Group 1 and Group
2 starting hold’em hands.
 Table
5 - Sklansky Group 3 Hands
Table
5 - Sklansky Group 3 Hands
|
99 |
*JTs |
QJs |
KJs |
ATs |
AQ |
There are 6 members of
S&M Group 3, as shown in Table __ (above).
 One
hand, JTs, doesn’t belong in the group. But KTs does. Also, the rank order of
each hand in the Grpup is slightly different than Sklansky suggested. These
changes have been reflected in Figure __ which is the rank ordered power hands
that fall in the 11th, 12th, 13th, 14th,
15th and 16th overall. positions
One
hand, JTs, doesn’t belong in the group. But KTs does. Also, the rank order of
each hand in the Grpup is slightly different than Sklansky suggested. These
changes have been reflected in Figure __ which is the rank ordered power hands
that fall in the 11th, 12th, 13th, 14th,
15th and 16th overall. positions
This discrepancy has the following potential
impact on player strategy.
S&M recommend playing only Group 1-3 hands
in a tough game from early position. If you follow this recommendation, you
should fold JTs from an early
position in a tough game, and start
playing KTs instead.
So, that’s it for the Sweet 16. Did Sklansky get
them right?
In terms of group membership, only 1 hand out of
the 16 needed to be replaced, although error of ranking within groups tended to
increase. In fact, as we shall see, this error becomes even greater as we move
down into the area of Expert playing hands.
In terms of stated rationale for various
raising/calling strategies, however, there was considerable error among these
very best of hands.
The Expert 24 and the Medium
Suited Connector Myth
When we add the next
highest ranking 8 cards to the Sweet 16, we reach what we consider to be the
smallest playable subset of starting hands.
In doing so, however,
we encounter what we have chosen to call the “Medium Suited Connector myth.”
Like most myths, it contains some elements of truth. But the truth has
been blown way out of proportion.
Figure 6 - Sklansky Group 4 Hands
|
*T9s |
KQ |
88 |
QTs |
*98s |
*J9s |
AJ |
*KTs |
There are four hands
in S&M’s Group 4 that do not belong. In the case of one of these, KTs, it
got moved up to Group 3 and was replaced by JTs, which was demoted from Group
3. This was a relatively minor adjustment in hand rankings.
But we are left with 3 suited connectors (T9s,
98s and J9s), the valiues of which keep being rediscovered every year or so,
but whose true values have not been put in perspective in practical terms for
the regular hold’em poker player.
 We
need to consider here the overall context, to look at all of the medium suited
connecotrs together, to gain some perspective.
We
need to consider here the overall context, to look at all of the medium suited
connecotrs together, to gain some perspective.
Figure ___ shows the rank for each medium (and
small) suited connector, starting with T9s and working down through 54s. The
mean rank of these hands is shown for each of Tables 1, 2, 3, 4 and 5.
 You
will note that the classic 10-player showdown results (T5) show a very simple,
linear deterioration in the relative rank order of these starting suited
connectors as the value of the top card gets smaller. This was discovered
sometime around 1972.
You
will note that the classic 10-player showdown results (T5) show a very simple,
linear deterioration in the relative rank order of these starting suited
connectors as the value of the top card gets smaller. This was discovered
sometime around 1972.
A few years later several people discovered that
some of the smaller suited connectors (such as 87s and 76s) sometimes played
better than their larger cousins (such as T9s). This reversal of the 10-player
showdown results was both surprising, and held as a professional holdem
players’ trade secret by many. This U-Shaped effect is clearly visible in the
HE Table 1 results shown in Figure____.
The problem is that playing in the extremely
tight games, such as those we characterize here by HE Table 1, it is difficult
to make any money: the pots are small (which is the natural consequence of
tight players), and these medium suited connectors, even though they improve
dramatically, never rise to the level of being powerhouse starting hands.
In fact, as the games become looser there is a
clear trend visible in Table ___ for the showdown linearities to dominate. Even
if you think you’re playing under the ideal conditions for medium suited
connectors, if one player leaves or a new player joins the game your assumption
may suddenly no longer be correct and intertia could easily lead you to end up
playing what are just relatively weak
hands.
Another thing that is potentially dangerous is
to rely on various “probe” software packages common available today that allow
you to pit one hand against another to a showdown, seeing which of them is
better.

![]() These
would be fine, and the results reliable, so long as there do not exist any
underlying non-linearities of the type visible in Figure __ for medium suited
connectors. But we DO know that assjmption is incorrect, and it has been known
to be incorrect in the poker literatures for decades. We recommend that, unless
you already know the answers to the questions you’re seeking and simply want to
be precise, you do NOT use isolated one-on-one type simulations at all (the
U-Shaped function we’ve already discussed is not the only one in the underlying
fabric of Texas hold’em).
These
would be fine, and the results reliable, so long as there do not exist any
underlying non-linearities of the type visible in Figure __ for medium suited
connectors. But we DO know that assjmption is incorrect, and it has been known
to be incorrect in the poker literatures for decades. We recommend that, unless
you already know the answers to the questions you’re seeking and simply want to
be precise, you do NOT use isolated one-on-one type simulations at all (the
U-Shaped function we’ve already discussed is not the only one in the underlying
fabric of Texas hold’em).
Turning back now to the Sklansky Group 4 hands,
we need to replace the 4 deviant hands by better ones.(A8s, A9s, JTs and AT).
Because the T4 and T5 HE Table conditions still have positive power ratings two
of these (J9s and T9s) have a high enough overall power index to just be
demoted to Group 5 while the third (98s) slips down to Group 6.
The
Starving Play List
We come now to our first overall recommendations
regarding limit hold’em play strategies. We call it the “Starving Play List”
because it should be appropriate to the most risk-averse, or conservative
player.
ü Pick
your 10-player HE Table carefully. Look for players who seem to be having fun,
and where at least half of the stay in to see the flop. Table selection is a
major determinant of how well your hands will hold up in the long run.
ü
Play only the top 24 hands, as shown in
Figure__ thru__. Be sure to note that the figures indicate groups rather than
particular hands. That is AdTd means ATs, and
KcQh means any KQ except KQs, etc.
In poker, when every other player knows what
your hand is, you suffer tremendous disadvantage. Just playing good cards is
not sufficient, nor is raising AA and KK only. You need a carefully planned but
hard to read raising strategy. We suggest using what we call a “parallel game” plan.
Suppose you play lower limit games like 3/6,
5/10/, 6/12 and 10/20, but would play other games such as 6/6 or 10/10 if they
were spread.
You can decide to play two different limit games
at the same time, at the same table, simply by having the following betting
strategy: play hands 1-12 at a $10/$10
HE Table, while hands 13-24 you play at the $5/$10 HE Table. This is quite
simple. You just decide to always raise hands 1-12, and never raise hands
13-24. Otherwise, make appropriate other adjustments in your response to raises
by other players before the flop. You can also adjust the fraction of hands you
play that you’ll raise, and so on.
The Starving Play List will allow you to play
about 3 hands per hour under typical playing conditions. Very conservative, but
it will require a great deal of patience.
The
Tight Expert’s Play List
If you’d like to play more hands, and are an
experienced player, then consider the “Tight
Expert’s Play List”, which adds the hands that belong to a corrected
Sklansky’Group 5.
The original members of Sklansky’s Group 5,
arranged in the order suggested by S&M, are shown below in Table __.
Figure 9 - Sklansky's Group 5 Hands
|
77 |
*87s |
Q9s |
*T8s |
KJ |
QJ |
JT |
*76s |
*97s |
|
*A9s |
*A8s |
A7s |
A6s |
A5s |
A4s |
A3s |
A2s |
*65s |
There are 18 hands in Sklansky’s Group 5. But 7
of these belong elsewhere. Two (A9s, A8s) deserved promotion to Group 4, as we
have already seen.
 The
five remaining hands are weak suited connectors, and “semi-connectors” (T8s,
97s, 87s, 76s and 65s). We have already discussed the error associated with
over-rating the nonlinearities in these hands, especially 87s and 76s.
The
five remaining hands are weak suited connectors, and “semi-connectors” (T8s,
97s, 87s, 76s and 65s). We have already discussed the error associated with
over-rating the nonlinearities in these hands, especially 87s and 76s.
But these are also among the most sensitive
hands to both number of foes and overall tight/loose HE Table playing
conditions. 65s, for example, ranks 25th (out of 169) in sensitivity
to HE Table conditions, 24th in sensitivity to number of foes at the
river and 29th in sensitivity to interactions between these factors.
![]() Indirectly,
as a result of their (a) extreme power nonlinearities and (b) extreme
sensitivity to HE Table playing conditions, these hands drop out of the top 84
starting hands entirely. In typical limit hold’em casino games at mid and lower
limits, these hands should be folded by the advanced player.
Indirectly,
as a result of their (a) extreme power nonlinearities and (b) extreme
sensitivity to HE Table playing conditions, these hands drop out of the top 84
starting hands entirely. In typical limit hold’em casino games at mid and lower
limits, these hands should be folded by the advanced player.
The three others (87s, 97s and T8s) are simply
demoted. T8s goes to Group 6 while 87s and 97s get moved down to Group 7.
The 7 additions to Group 5 include two (KT and
QT) that are obviously closely related to three original members (KJ, QJ and
JT) and five higher ranking suited hands (K9s, K8s, Q8s, T9s and J9s) than the
small suited connectors they replace. This is because with suited starting
hands the rank of the kicker is usually more important than the connected-ness
of their values, although with T9s both factors may combine.
If you otherwise
follow the S&M guides to poker strategy, some of these changes would impact
how you play the game. For example,
“…some hands, such as 87s..play well
against many opponents. If there are usually a lot of callers ... these types
of hands become playable in early position. However, over playing these hands
up front (and most players do just that) can get you into trouble.” (S&M,
p.15).
87s is now a Group 7 hand, which S&M do not
recommend for play in early position at all. The problem, of course, is that
recommending the play of 87s against “many” opponents, without specifying
exactly how many or the consequences of not counting accurately, is not clear
guidance. S&M do, however, provide themselves an out by the observation
that “most players” over play these
hands.
We would agree both with (a) not playing Group 7
hands in early position and (b) that anybody who does is over playing them.
You will be dealt one of these starting hands,
ranked 1 to 42 globally, about once in every 5 hands. This means you should be
involved in about 6 pots per hour. We consider this to be the Tight Expert’s Play List.
The
Professional’s Play List
We turn now to Sklansky’s Group 6 hands, as
shown in Table __ below.
Table 6 - Sklansky's Group 6 Hands
|
66 |
*AT |
*55 |
*86s |
*KT |
*QT |
*54s |
*K9s |
J8s |
There are 9 members of S&M’s original Group
6. Four of these have already been promoted: AT to Group 4, and three (K9s, KT
and QT) up to Group 5. One (55) deserves demotion to Group 7.

A medium 1 gap suited connector (86s) is dropped
from the list of playable hands entirely. It has a power profile across HE
Table conditions similar to those discussed earlier as Group 5 deviant suited
connectors. Also, it’s the 86th ranking hand overall.
 We’ve replaced these 7 changes with the highest
available power ratings (T8s, K7s, 98s, A9, K6s, K5s and A8). Some of these are
demotions from higher Sklansky Groups as described previously.
We’ve replaced these 7 changes with the highest
available power ratings (T8s, K7s, 98s, A9, K6s, K5s and A8). Some of these are
demotions from higher Sklansky Groups as described previously.
These starting hands, ranking from 1 up to 51,
constitute 24% of all starting hands. If you follow this Professional’s Play List, you’ll bet in about 1/4th
of the pots at your HE Table. But, choose your HE Table with care. Leave tight
games or change your strategy.
The
Savvy Gambler’s Play List
We turn now to Sklansky’s original Group 7
hands, as shown below in Table ___.
Table 7 - Sklansky's Group 7 Hands
|
*44 |
J9 |
*43s |
*75s |
T9 |
*33 |
*98 |
*64s |
*22 |
|
*K8s |
*K7s |
*K6s |
*K5s |
K4s |
K3s |
K2s |
Q8s |
|
There are 17 hands in this Group. Unfortunately,
11 of these do not belong here.
The two low pairs, 22 and 33 are not worth
playing. Group 8. They have been dropped from all our play lists entirely.
Neither are the small suited connectors, 64s, 43s, 75s or the connector 98.. The
pair, 44, is demoted down to Group 8.

Suited medium Kx’s have been under valued by
S&M, and each of these deserves promotion out of Group 7: K8s up to Group
5, while K7s, K6s and K5s were promoted up to Group 6. S&M had originally
placed all Kxs from K2s through K8s into this single Group.
We also recommend a slightly different playing
strategy with the corrected Group 7 hands.
![]() S&M
recommend Group 7 only when you’re on the Button, with one or more callers in
front. In particular, they recommend raising with the small pairs or small
suited connectors. But all of these hands have either moved down to Group 8 or
taken entirely off the play lists. Each depended on hitting the flop with trips
or a flush/straight draw. It turns out, however, there is more value in hoping
to hit the flop for a King-high flush draw.
S&M
recommend Group 7 only when you’re on the Button, with one or more callers in
front. In particular, they recommend raising with the small pairs or small
suited connectors. But all of these hands have either moved down to Group 8 or
taken entirely off the play lists. Each depended on hitting the flop with trips
or a flush/straight draw. It turns out, however, there is more value in hoping
to hit the flop for a King-high flush draw.
If there is merit in the S&M strategy for
Button raises with Group 7 hands in general, then, you should consider each of
these hands for the following decision paths: either call unraised pots in late
position, raise an unraissed pot from the Button or otherwise fold these Group
7 hands. If you’ve played one then wait for the flop and, if you haven’t made a
hand such as a flush draw, trips or two pair, fold.
The Savvy
Gambler will have these hands in his/her Play List knowing both that they
are good hands with a good flop, that foes generally discount the liklihood
you’ll be holding them thus encouraging action when the flop doesn’t look too
scarey, and he/she will have the iron
discipline to discard them on those many rounds when the flop goes elsewhere.
The gambling part of this Play List is in the
need to pray, or otherwise invoke the Poker Gods, for a suitable flop more than
with hands in the other groups.
By adopting the Savvy Gambler’s Play List,
without regard to your position, you would on average, participate in about 1/3rd
of all pots at your HE Table. The actual number will fall in the range of 1/4rd
up to 1/3rd because of raising by other players and your
opportunities for late play of these hands. As is true in general, of course,
stay away from very tight HE Tables.
The
Gambler’s Play List
We turn now to the Group 8 hands which, when
added to all of the previous Play Lists, constitute up to 44% of all hands
dealt in Texas Hold’em.
Table 8 - Sklansky Group 8 Hands
|
*87 |
*53s |
*A9 |
*Q9 |
*76 |
*42s |
*32s |
*96s |
|
*85s |
J8 |
*J7s |
*65 |
*54 |
*74s |
*K9 |
T8 |
 There
are 16 hands in S&M’s original Group 8. Of these, only 2 belong in the
group.
There
are 16 hands in S&M’s original Group 8. Of these, only 2 belong in the
group.
Four hands deserved promotion: A9 was moved to
Group 6, while K9, Q9, and J7s were moved to Group 7.
 Otherwise,
all of the remaining changes are demotions out of the Play Lists entirely.
Examples are the medium connectors 87, 76, 65 and 54, and the small suited
connectors 53s, 42s and 32s. While these hands can sometimes hit ideal flops,
and might be played occasionally for surprise value, they are not robust enough
overall for us to recommend their play even on the Gambler’s List.
Otherwise,
all of the remaining changes are demotions out of the Play Lists entirely.
Examples are the medium connectors 87, 76, 65 and 54, and the small suited
connectors 53s, 42s and 32s. While these hands can sometimes hit ideal flops,
and might be played occasionally for surprise value, they are not robust enough
overall for us to recommend their play even on the Gambler’s List.
The Jones’ Combinations
Lee Jones, in his book “Winning Low Limit Hold’em,” does not rank all playable
hands, so we will have to take a slightly different approach to evaluating his
recommendations.
Early
Position
Raise with AK, QQ and JJ if “..it will limit the field.” We would strongly
urge raising with AK for this purpose, as we have seen. The value of AK
deteriorates dramatically as the number of realistic foes increases beyond one
at the river. But QQ and JJ actually hold
up well, so if you raise these hands it should be for value rather than to
limit the field.
“Always re-raise with AA and KK”.
Yes, we agree entirely.
Table 9 - Jones Early Position Hands
|
AA |
KK |
QQ |
JJ |
TT |
AKs |
KQs |
QJs |
*JTs |
|
AQs |
KJs |
*QTs |
AJs |
KTs |
AK |
*KQ |
AQ |
*AJ |
The table above shows 18 hands that Jones
recommends for early position play. If we assume that these would be the top 18
ranked hands in the game, then 4 of these do not belong: QTs, JTs, KQ or AJ. In
their place should be ATs, AQ, 99 and 88.
But Jones goes on to say that “..if
the game is loose-passive add..”
99, 88, 77, 66, 98s, 87s, QJ, JT, T9, and 98 to the list above.
These should be the 19th thru 28th
ranked hands. Unfortunately, we show little correspondence with these
recommendations.
So far, of 28 starting hands recommended by
Jones we would agree with only about half. This is substantially less than for
Sklansky and Malmuth. We leave it as a reader’s exercise to work out the
details to compare our rankings with what we have to assume must be Jones’
rankings.
Wrap-Up
We have, during the course of examining in
detail the hand rankings of Sklansky and Malmuth, as put forth in their book, “Hold’em Poker For Advanced Players,”
updated and revised their rankings and reasons for playing or raising some
starting hands. We’ve also presented five overall playing strategies for you to
consider, in the form of Play Lists.
Table 10 - The 5 Play List Strategies
|
Personality |
Play |
Threshold |
|
Starving |
11.3% |
Top
24 hands |
|
Tight
Expert |
20.0% |
Top
42 hands |
|
Professional |
24.0% |
Top
51 hands |
|
Savvy
Gambler |
32.9% |
Top
68 hands |
|
Good
Gambler |
43.9% |
Top
84 hands |
Why not just wait for AA and only play it,
folding every other hand that you are dealt?
Because of the need to post blinds in hold’em,
you pay for playing at the rate of about 4 ½ small bets (4.5sb) per hour, If you waited only for AA, you’d be waiting
an average of 5-7 hours to play one hand at a cost of 27sb. This is a fairly
good net pot to win, just to break even … assuming AA always won, which of
course it doesn’t.
Hold’em is structured so that you must play to win.
Each of the recommended Play Lists should suit
some hold’em player. But playing any one of them will require patience and
discipline.