|
A major barrier to reusability and interoperability of knowledge-based systems is semantic heterogeneity: different applications, databases, and agents may ascribe disparate meanings to the same terms or use distinct terms to convey the same meaning.
It has been recognized that the emerging technology concerned with the development and application of ontologies will play a central role in achieving semantic integration and reusability ([6],[7]). An ontology is a computer-interpretable specification that is used by an agent, application, or other information resource to declare the vocabulary of terms it uses, together with an axiomatization of the meaning for the terms in some formal logical languauge. Ontologies support the semantic integration of software systems through reasoning with this axiomatization ([2],[4]).
Much of the existing work on ontologies ([5]) has focused on the use of languages with limited expressiveness, such as description logics. Nevertheless, in many systems that use ontologies with limited expressiveness, it is necessary to introduce extralogical assumptions in order to capture the intended semantics of the ontology's terminology. Thus, the interoperability issues that arise within realistic settings typically require languages with the expressiveness of first-order logic.
The Process Specification Language (PSL) ([1],[3]) has been designed to facilitate correct and complete exchange of process information. (As of June 2004, PSL has been accepted as an International Standard (ISO 18629) within the International Organisation of Standardisation.) The PSL Ontology is a set of theories in the language of first-order logic. All core theories within the ontology are consistent extensions of a theory referred to a PSL-Core, which introduces the basic ontological commitment to a domain of activities, activity occurrences, timepoints, and objects that participate in activities. There is also a set of theories referred to as PSL Outer Core (see Figure 1), which supports the explicit representation of state, concurrency, and complex actions. In particular, one of the theories in PSL Outer Core is equivalent to the first-order theory of Reiter's axiomatization of the situation calculus. Additional core theories capture the basic intuitions for the composition of activities, and the relationship between the occurrence of a complex activity and occurrences of its subactivities.
Figure 1: The theories of PSL Outer-Core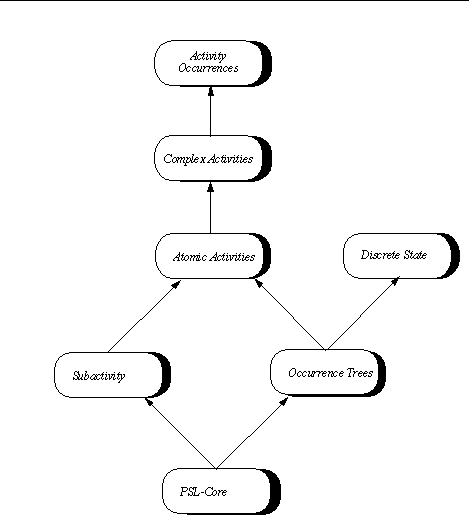
The PSL Ontology is the basis for the first-order axiomatization of
semantic web services in FLOWS. In particular,
the FLOWS Process Model incorporates the following concepts and features
from PSL:
The model theory of PSL provides a rigorous abstract mathematical characterization of the semantics of the terminology of ontology. This characterisation defines the meanings of terms with respect to some set of intended interpretations represented as a class of mathematical structures. Furthermore, for each theory in the PSL-Ontology, there are theorems that prove that every intended interpretation is a model of the theory, and every model of the theory is isomorphic to some intended interpretation.
This first-order semantics has several advantages. Since complex activities and their occurrences are elements of the domain, PSL sentences can explicitly describe and quantify over complex activities. This makes it possible to express in an explicit manner a broad variety of properties and constraints on composite activities. Service design analysis and verification can therefore be expressed as inference problems that are solved by inference techniques that are sound and complete with respect to models of the theories. Also, a process ontology with a first-order axiomatization can be more easily integrated with other ontologies (which are almost all first-order theories themselves). Other approaches to process representation lack one or more of the formal properties of the PSL Ontology -- many ontologies do not provide a model theory; those that do specify a formal semantics, typically do not provide an axiomatization of this semantics.
PSL has already proven useful as exchange language between manaufacturing and business process software applications. Similar techniques can be used to integrate the diverse range of existing research efforts in semantic web services.