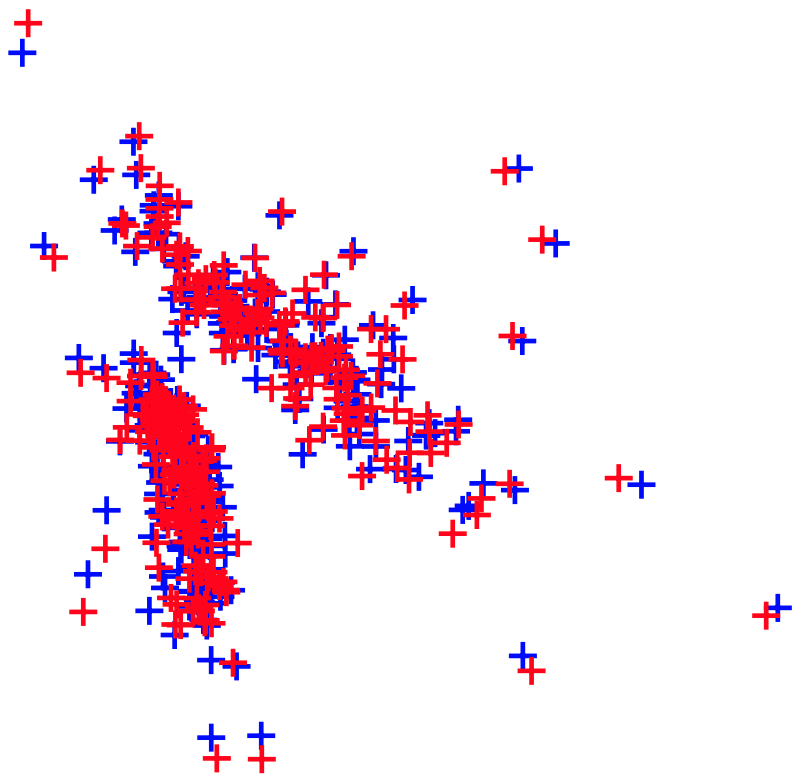
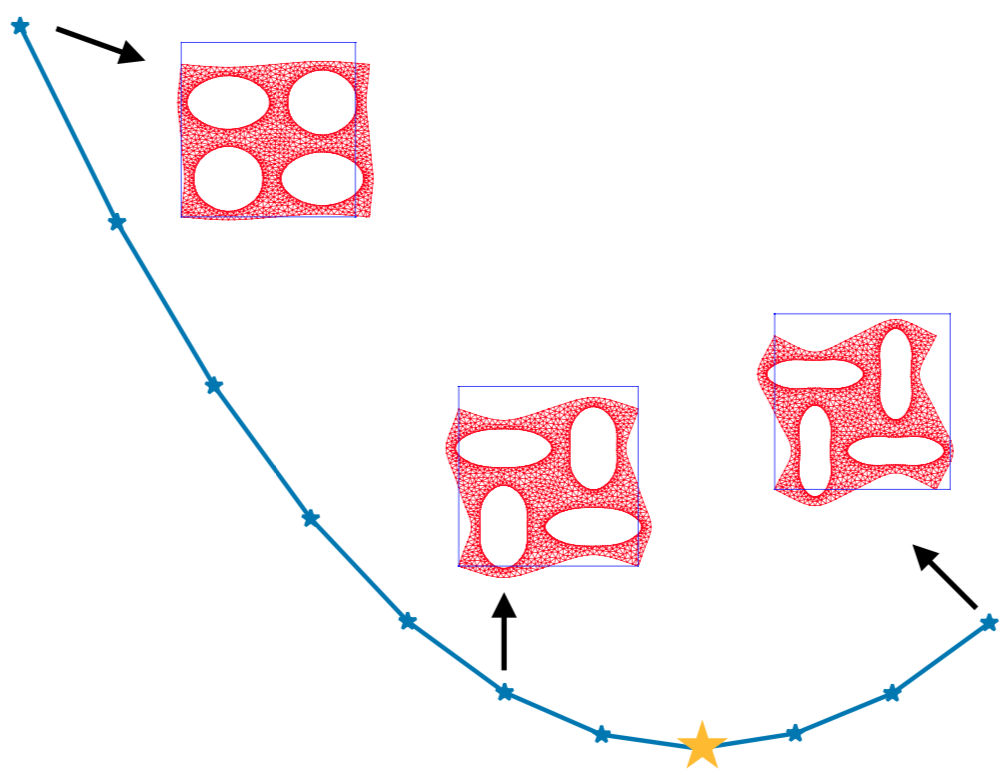
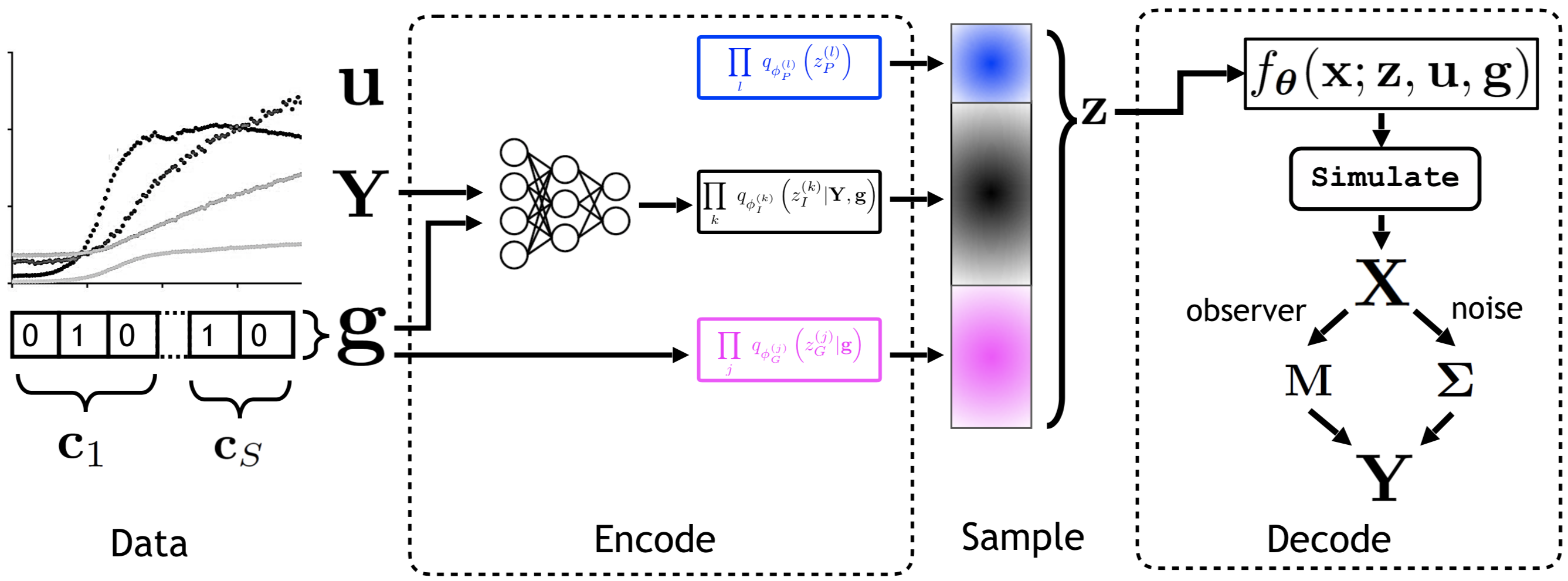
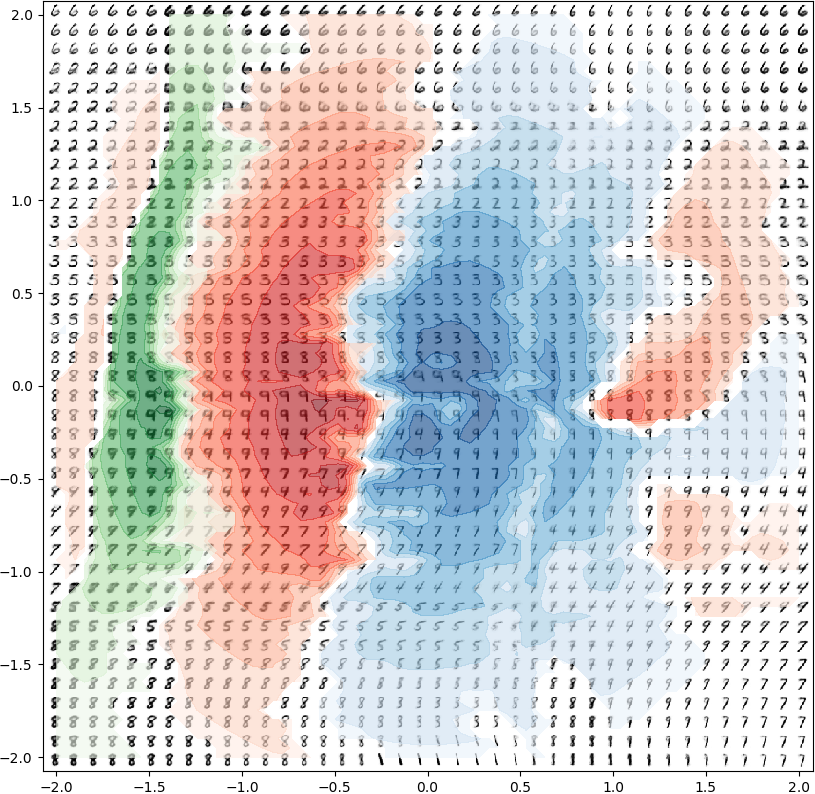
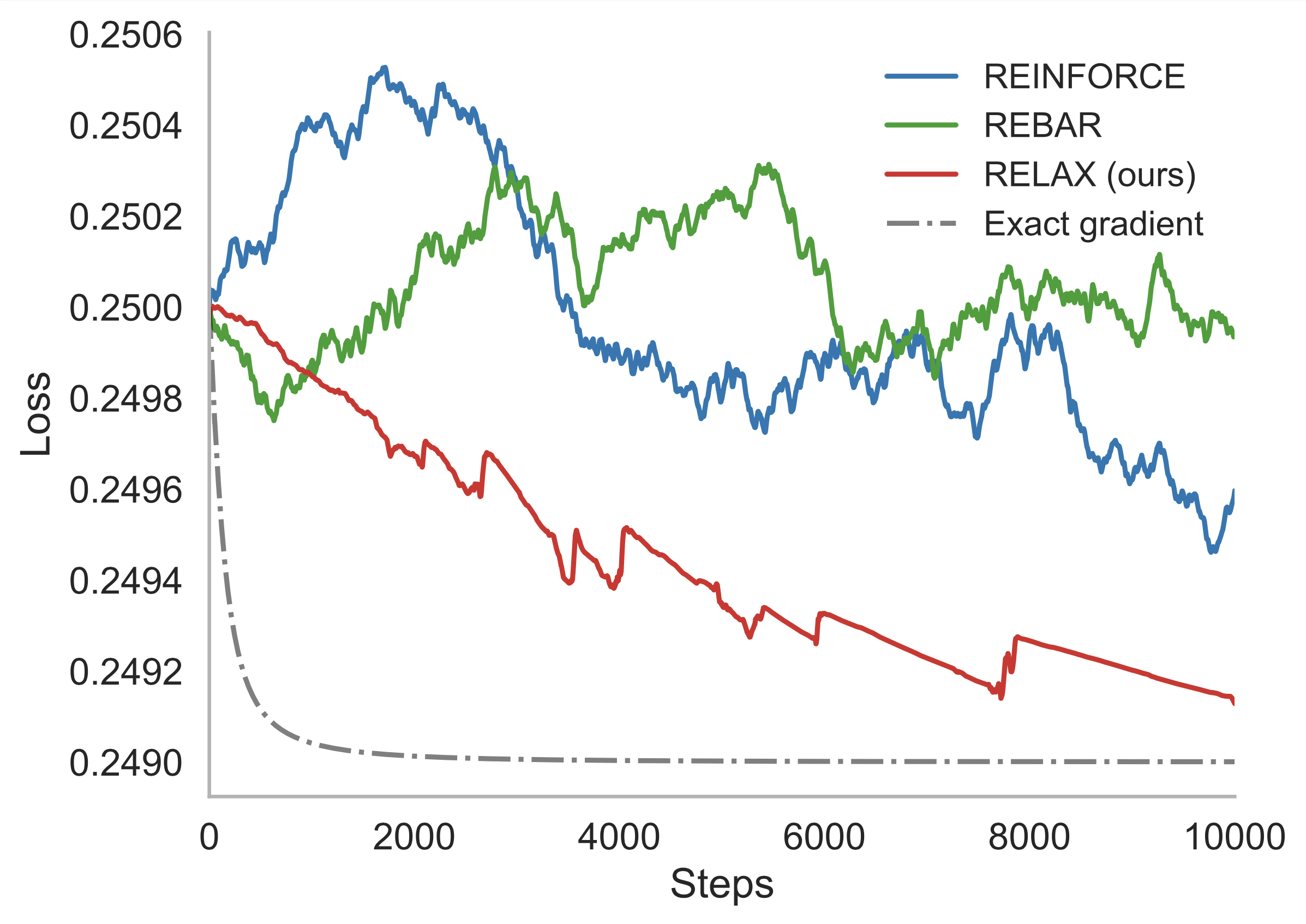
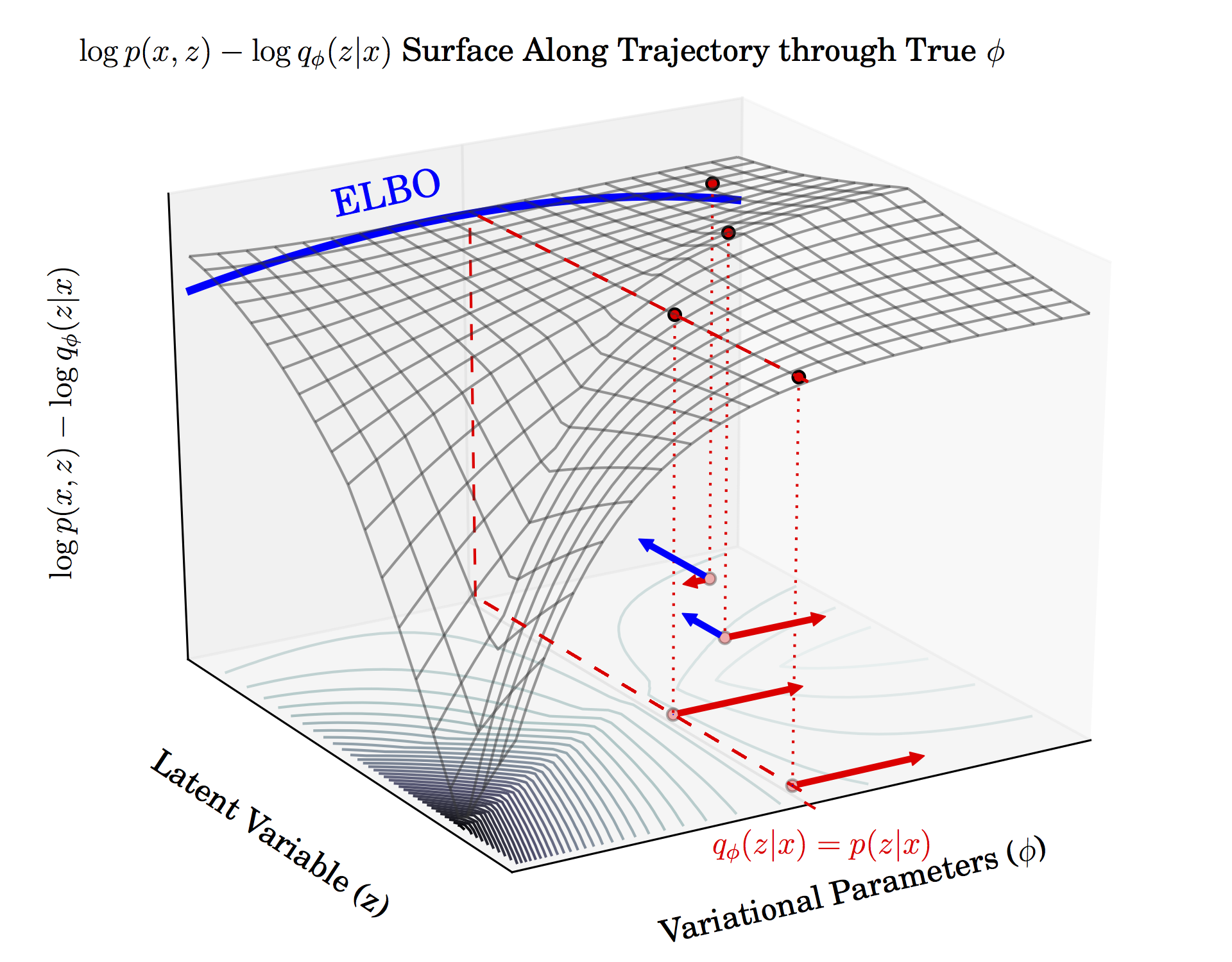
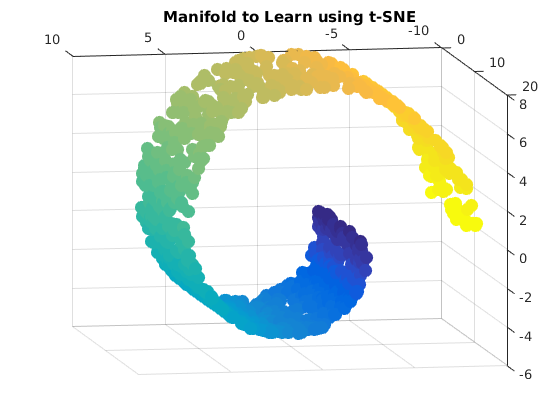
I am a PhD student at Princeton working on statistical machine learning
advised by Ryan Adams,
in the Laboratory for Intelligent Probabilistic Systems.
In 2018, I completed my MSc with David Duvenaud at the
Vector Institute for Artificial Intelligence, while a student in Machine Learning group at the University of Toronto.
I completed my BSc (2016) at the University of British Columbia in Statistics and Computer Science advised by Mark Schmidt
I spent fall 2017 working with Ferenc Huszár on improving black-box optimization methods for general non-differentiable functions. During summer 2018, while an intern at Microsoft Research Cambridge, I collaborated on a novel class of deep generative models for understanding and programming information processing in biological systems. During summer 2019, while an intern at Google Brain, I collaborated with Durk Kingma on identifiable representation learning by deep discriminative models. In fall of 2019, I joined X, the Moonshot Factory (formerly Google X) as a Resident in core ML. Since February 2020, I have been a 20%-time Resident with the Quantum group at X, working on Bayesian inference for noisy intermediate-scale quantum algorithms.
Broadly, I aim to help push forward a theoretical understanding of deep learning in support of robustness, reliability, and efficient inference, with an overarching goal of improving scientific discovery and engineering design through leveraging new affordances in deep generative models.
Research
Email: roeder@princeton.edu
I spent fall 2017 working with Ferenc Huszár on improving black-box optimization methods for general non-differentiable functions. During summer 2018, while an intern at Microsoft Research Cambridge, I collaborated on a novel class of deep generative models for understanding and programming information processing in biological systems. During summer 2019, while an intern at Google Brain, I collaborated with Durk Kingma on identifiable representation learning by deep discriminative models. In fall of 2019, I joined X, the Moonshot Factory (formerly Google X) as a Resident in core ML. Since February 2020, I have been a 20%-time Resident with the Quantum group at X, working on Bayesian inference for noisy intermediate-scale quantum algorithms.
Broadly, I aim to help push forward a theoretical understanding of deep learning in support of robustness, reliability, and efficient inference, with an overarching goal of improving scientific discovery and engineering design through leveraging new affordances in deep generative models.
Research
Email: roeder@princeton.edu