CSC 148H - Assignment #4 - Graphs

Due Date: Friday August 1st, 1pm.

 

This assignment requires that you do some independent reading. Before trying to understand the assignment statement below, you should read and understand sections 7.6 - 7.6.3 of your text book. Without this background, some of the details below may seem cryptic.

Part 1: Substring Searching

The following is known as the "substring searching" problem. You are given two strings, S and S', which are composed of characters from an alphabet, and you have to find the index of the first occurrence of S in S'.


For example: find the index of the first occurrence of “fun” in “programmingisafunactivity”. In this case, the answer is 14. 

 

The substring (S) we are searching for is known as the search string, and the string we are searching (S') is known as the text string. In the above example, the search string is “fun” and the text string is “programmingisafunactivity”.

 

Substring Searching with a DFA

 

There are a number of ways to solve the substring searching problem. The naive approach (detailed in section 7.6.2 of your text) involves checking for the search string starting at each character in the text string until the search string is found or the end of the text string is reached. This method, however, is extremely inefficient. Another approach involves using a special type of graph, known as a Deterministic Finite Automaton (DFA). This approach is much more efficient, as it solves the problem in linear time with respect to the size of the text string. (This doesn't include the cost of first building the DFA, however.)


A DFA represents the search string pattern as a graph where each vertex in the graph is a state, which identifies how much of the search string pattern has been recognized, and each edge in the graph identifies a transition for one or more characters in the alphabet.

 

For an example of a DFA, see Figure 7.40 on page 337 of your text. Keep in mind that this figure illustrates the DFA for the search string “ACATA” and the alphabet being used is composed of the letters “A”, “C”, “G” and “T”. In this example DFA, vertex 3 and edge “C” transitions to vertex 2.


Note that every vertex (with the exception of the terminating vertex) must have a transition edge for each letter in the alphabet. 


In order to find a search string in a text string using a DFA, initialize the DFA by setting its current state to the start state (state 0).  After the DFA is initialized, scan through the text string character by character, updating the state of the DFA after each character is read by following the appropriate transition edge. Each state of the DFA represents the portion of the search string that has been matched so far. Initially you start in state 0, meaning that no part of the search string has been matched yet. After you encounter the first character of the search string in the text string, you enter state 1, which means the first character has been matched. If the next character in the text string is the same as the next character in the search string, you move to state 2, indicating that you've matched the first two characters, and so forth. In general, if you are in state i, this means that you will have matched the first i characters in the search string. If you enter the DFA's final state before reaching the end of the text string, then the search string is a substring of the text string. Otherwise, the search string is not a substring of the text string.

 

Representing DFAs

 
In lecture we discussed two different ways for representing graphs: adjacency matrices and adjacency lists. In an adjacency matrix, each row and column of the matrix represents a node in the graph. An entry at position (i,j) represents an edge from node i to node j. If entry (i,j) is 1, then this means that there's an edge from i to j in the graph, and if it's 0 then there is no edge from i to j. In an adjacency list, each node maintains a list of nodes to which it is adjacent. This representation is more efficient than an adjacency matrix, since space is used only for the edges that are actually present in a graph.


One way that we could represent the DFA is using a standard adjacency matrix. The characters used for transitioning from node i to node j are stored as a set in entry (i,j); if there's no edge (and hence no way to transition) from node i to node j, then the set is empty. This representation leads to some efficiency issues in the way that we use the DFA, however. Given a state in the DFA, and a transition character, how do we find the next state after a transition? Using the adjacency matrix just described, we would have to search through every entry in row i of the matrix until we found an entry that contained the transition character.  This isn't particularly efficient. Trying to represent a DFA using a standard adjacency list approach also has problems.


Instead, to represent a DFA, we will use a transition matrix. Each row in a transition matrix represents a node in the DFA, and each column represents a transition character (i.e., a label on an edge). Entry (i,j) represents the node to which the DFA transitions from state i with transition character j. For example, in the DFA in figure 7.40 of your text, entry (1,G) = 0, entry (1,C) = 2, entry (1,A) = 1, etc. 

 

You only need as many columns in your transition matrix as there are characters in your alphabet. For example, given an alphabet { ‘A’, ‘B’, ‘C’, ‘D’ } and a graph with 3 vertices, the transition matrix would look like this (excluding the matrix entries that represent the vertex you transition to):

 

 

‘A’

‘B’

‘C’

‘D’

0

 

 

 

 

1

 

 

 

 

2

 

 

 

 

 




Using this representation makes it very easy (and very fast) to determine the next state after a transition.


Constructing the DFA


Before you can perform a substring search using a DFA, you have to first construct the DFA. The DFA is constructed based on the search string and an alphabet. The following pseudocode does the construction assuming that you are using a transition matrix to represent the DFA.


n = length(search_string)

construct a transition matrix so that it has n+1 rows and a column for each character in the alphabet

initialize each entry in the transition matrix to be 0

mark vertex 0 as the start state and vertex n as the final state

for i in range(n+1):
    for each c in the alphabet:
          k = min (n, i+1)
          while search_string[:k] is not a suffix of search_string[:i]+c:
                  k = k - 1
          transition_matrix[i][c] = k

The details of why this procedure works are beyond the scope of the assignment (and this course). If you are interested, you can read more about this construction in chapter 32.3 of "Introduction to Algorithms" (Second Edition) by Cormen et al. (You have free access to this textbook online through the UofT library website.)

Some points of clarification:
        


The DFA class

Your job is to implement substring searching using the DFA approach. The starter code is in DFA.py. This module contains a class DFA, which defines the following methods (that you have to implement):

 class DFA:

  1. __init__( self, search_string, alphabet ): given the search string and alphabet, initialize the DFA graph using the construction algorithm we detailed earlier in this document . 
  2. find_substring( self, test_string ): return the start index of the first occurrence of the search string in the test string, test_string. Return -1 if there is no occurrence.

 

Part II: Spelling out Shortest Paths

In this part, you will implement code to find the shortest path between two vertices in an unweighted graph. Graphs can be directed or undirected. Furthermore, edges in the graph are labelled with characters.  Consider the example graph below:





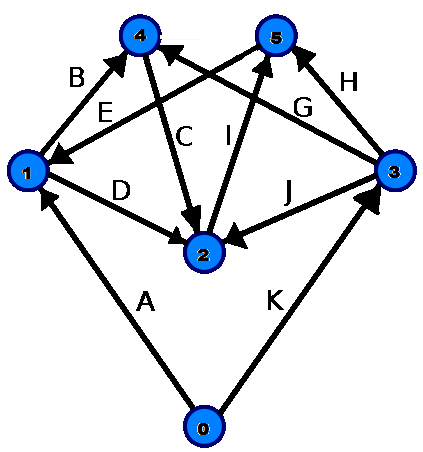
By labelling the edges in the graph with characters, we can associate a word with any path between two vertices. More precisely, given a path from v1 to v2, the path's associated word is composed of the letters that label the edges on the path from v1 to v2.


Your job will be to find the word spelled out by the characters labelling edges on a shortest path between two vertices. For example, in the graph above, the shortest path from vertex 2 to 1 goes through vertex 5 and spells out the word IE. If there is more than one shortest path between vertices, you have to find the path whose associated word is lexicographically the smallest. For example, the path from vertex 0 to vertex 2 can go either through vertex 1 or vertex 3 (i.e., the paths 0,1,2 and 0,3,2 are both shortest paths from vertex 0 to vertex 2). However, the path through vertex 1 spells out AD, which is lexicographically smaller than the word spelled out by the path through vertex 3, KJ. (For our purposes, a word w_1 is 'lexicographically smaller' than w_2 if w_1 would appear in the dictionary before w_2.)


Graphs are represented using adjacency lists. The implementation is provided for you in the Graph class in graph.py. It is a very minor variant of the adjacency list implementation we saw in lecture. In each vertex v's adjacency list, instead of simply storing the adjacent vertices, we store 2-element tuples, where the first element is an adjacent vertex v2, and the second element is the character labelling the edge from v to v2.  For example, in the adjacency list of vertex 0 in the above graph, we store [(1,'A'), (3,'K')].


Your code will go in the file pathfinder.py. You have to implement the following method, which is defined in the starter code:


Hints/Tips/Assumptions

 

Side Notes Regarding Proper BBS Usage


Just a friendly reminder about proper BBS usage. We encourage you to post questions on the bulletin board if you are having problems, but please do not post questions (or answers) that reveal any part of your solution (whether or not you think it's correct). This applies to all parts of the assignment, no matter how small (e.g., testing if a string is a suffix of another).


Also, to ensure that questions are properly answered by the TA in advance of the deadline and that no last minute confusion arises, please post your questions by no later than July 31st, 4pm.

 

Summary of Deliverables

 

The following is a list of files you need to submit and the methods that are defined in the starter code. Most of these methods still need to be implemented by you. Be careful to not change any method definitions or attribute names in the starter code. Also be careful to obey the instructions with regards to what you should be returning from these functions, and what kinds of arguments the functions expect. This is important for automarking.  You are free to add any methods/functions/classes (or any other files) that you wish.

 

DFA.py - YOU MUST SUBMIT THIS FILE

 

class DFA:

 

pathfinder.py - YOU MUST SUBMIT THIS FILE

 

 
graph.py - This module contains an adjacency list implementation of a Graph class. Instances of this class are used as arguments to the shortest_path method defined above. YOU SHOULD NOT SUBMIT THIS FILE.

 

testDFA.py - YOU MUST SUBMIT THIS FILE


testpathfinder.py - YOU MUST SUBMIT THIS FILE


Mark Breakdown

Part 1 (40%)
    Automarking (50%)
    Unit Tests (20%)
    Commenting/Code style (30%)

Part 2 (60%)
    Automarking (50%)
    Unit Tests (20%)
    Commenting/Code Style (30%)


 

Be sure to start this assignment early!