Tic-Tac-Toe
is a game that, if played "perfectly" by both players, will always
result in a tie. In other words, you can implement an algorithm that
will never lose at Tic-Tac-Toe.
Game play is on a 3x3 board that is initially empty:
None | None | None
---------------------------------
None | None | None
---------------------------------
None | None | None
("None" represents an empty marker).
There are two players: The 'X' player and the 'O'
player. The 'X'
player moves first. When a player makes a move, he places his letter on
an empty cell in the board, and then it becomes the other
player's turn. This back-and-forth play proceeds until either one
player wins or a tie occurs. A player wins when he creates a row,
column, or diagonal that contains only his letter. A tie occurs when
there are no more empty cells on the board, and there is no row, column
or diagonal consisting entirely of X's or O's
The Tic-Tac-Toe playing board is stored internally
as a list of lists (a list with 3 lists, of which each has 3 entries)
in the Board class and the
entries of the board are either Marker.NONE,
Marker.X or Marker.O (see
board.py for the Board
class and the Marker enumerations.)
Computer players are represented by the AmateurPlayer and ProfessionalPlayer classes,
described in Part 1 and 2, respectively, below. Given the current state
of the game (as a Board object),
the player places the next X or O on the board and returns an updated Board object. The Tournament
class takes two players and pits them against each other in a game, or
series of games, of Tic-Tac-Toe.
In the first part of this assignment, you will implement a very naïve, rule-based Tic-Tac-Toe playing algorithm. You will then pit your algorithm against itself in a Tic-Tac-Toe tournament.
Your player, who happens to be an amateur, will
follow these simple rules:
The AmateurPlayer class'
highest-level method, play_turn,
takes in the current board state and returns an updated Board object with the next board state.
In order to know where to place its marker, play_turn
needs to call helper functions to decide which rule to apply,
and where
to apply them. One helper function is used for each rule above: play_win, play_block and
play_random.
In
order to decide which rule to apply, each of these helper functions
must scan the board to find their potential move, and if they find one,
they return 2-element (row, column) tuple signaling the position of the
move. If no move exists, then the helper function returns None.
Example: If the current
board state is
O | None | O
---------------------
X | None | O
---------------------
O | None | X
and it's O's turn to play, the following are the
valid return values for the play_win function
called by O’s AmateurPlayer object:
(0,1) and (1, 1). play_turn
should return a board state of either
O | O | O
---------------------
X | None | O
---------------------
O | None | X
or
O | None | O
---------------------
X | O | O
---------------------
O | None | X
When implementing each helper function, think about
identifying
different conditions which would satisfy the rule. For example, one of
the few conditions play_win should
search for is: "for each row, are there two of my pieces and none of
the opponents? If so, return the empty position."
Hint: Blocking your opponent's winning move requires the same strategy as scoring a win yourself. Think about analyzing columns, rows and diagonals.
Create a number of suitable unit tests to convince
yourself (and us) that you have implemented AmateurPlayer
and Board correctly. Create your tests in testamateur.py and
testboard.py, respectively. These files already
contain some simple tests to get
you started. You should write tests to ensure each method defined in
AmateurPlayer and Board is implemented correctly (see "Summary of
Deliverables" for exceptions to this). When testing the play_turn
and corresponding play_* helper methods in AmateurPlayer,
for our marking purposes, we don't expect you to exhaustively test the
methods with all possible board configurations. You should test 2
non-identical cases in which a player makes a winning move, 2
non-identical cases in which a player blocks his opponent, and a single
random
move. However, adding more unit tests for your
own testing purposes is fine and probably necessary.
Once you have your AmateurPlayer
class up and running, it's time to pit two amateur players against each
other. The Tournament class has a
run_game method that sets up two
players and gets them to play a game of Tic-Tac-Toe until the game is
over. X always plays first.
The Board class'
is_game_over method might come
in handy
here. Once a game is over, the Tournament
class records who has won or whether there was a tie. The run_tournament method runs many games and
prints the final stats for win/losses/ties.
In mathematical literature, the game of Tic-Tac-Toe it said to have been 'solved'. This is because mathematicians and computer scientists have been able to map out the entire space of possible board layouts for any Tic-Tac-Toe game and derive a strategy that will always lead to either a victory of a draw.
In
this part of the assignment, we will map out the entire space of
all possible Tic-Tac-Toe games using a special type of tree data
structure called a Game
Tree. Each node in the tree represents a potential
state of a Tic-Tac-Toe game. In particular, each node stores:
Board object with the
current game state it represents, Node class and is
implemented in node.py. generate_game_tree()
module
function, located in professionalplayer.py. It is up to
you to
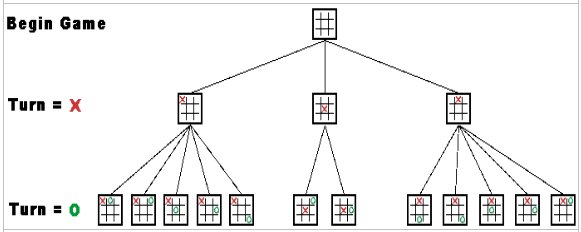
implement this function according to the procedure described below. An example of the first two plies of a (simplified) Tic-Tac-Toe game tree are illustrated below:

The tree in the image takes symmetry into account, however you will not be required to do so in this assignment. So, for example, the root node of your game tree will contain 9 children, each of which will contain 8 children, each of which will contain 7 children, and so on until a game is over (i.e. a node with a board layout representing a finished game will not have any children.)
More specifically, to construct the game tree you must perform the following tasks:
Note that we don't assign a ranking to the root
node.
The number of nodes in the game tree constructed
according to the above procedure turns out to be quite large (well over
100,000 nodes). You may find this surprising if you consider the number
of possible boards that
actually exist in Tic-Tac-Toe. To figure out the number of possible
boards, observe that there are only 3 markers that can be placed in
each cell (Marker.X, Marker.O, or Marker.NONE). So, there are 3 markers
that can be placed
in the first position. For each of these choices, there are 3 markers
that can be placed in the second position. For each of the 3x3 possible
configurations of the first two positions, there are 3 markers that can
be placed in the third position... and so forth. Since there are 9
positions on the board, there are 3^9 = 19683 possible board
configurations, some of which can't even arise in valid game play (e.g.
all X's or all O's).
The
reason that there are so many more nodes in the game tree than there
are Tic-Tac-Toe boards is because the game tree contains many duplicate
nodes. For
example, the same board will arise in the following two situations:
(i) X plays (0,0) then O plays (0,1) then X plays (0,2); (ii) X
plays (0,2) then O plays (0,1) then X plays (0,0). Because there are a
lot of duplicate nodes in the tree, this means that if the tree is
constructed naively, you will be doing a lot of repeated work.
Although naively constructing the tree is feasible
(it will take several minutes if you implement it correctly), there is
a much faster way of building the game tree. Essentially, you need to
use memoization. (See the lab from week 4, where you were introduced to
memoization.) Whenever you want to construct the subtree rooted at some
node, you first check in a "memoization dictionary" whether that node
already exists.
If it does exist, then the subtree rooted at that node is already built
and you don't have to build it again. Building the game tree
using
memoization means that more than one node in a given level may
reference the same child node, and that some nodes may have more than
one parent. Strictly speaking, such a structure is not a "tree"
according to the definition of a tree we discussed in lecture. We will
ignore this technicality, as it does not cause us any serious problems
for the way we use the game tree.
In order to use memoization, each node needs to
have a key associated with it, which will be used for looking up a node
in the memoization dictionary. The most natural choice for a
node's key is its board. However, the board is a list of lists, and
python does not let you use lists as keys in dictionaries. Instead, the
key will be a numeric representation of the board. This representation
can be obtained by calling the get_key method in the Board
class. (This method is already implemented for you.)
The ProfessionalPlayer
class has a play_turn
method, that (as with the AmateurPlayer class)
takes as input the current state of the game (again, a Board object) and uses the game tree
to make the next move: this method searches through the game tree for a
node with a Board object with
the same configuration as the current state (you can use the ==
operator to test equality between boards, since the
__eq__ method is defined in Board). Once the node
is identified, set the
next move by searching through the node's children and identifying a
board with a rating equal to the player's
piece (or a tie, if no winning options exist.) There's actually a much
quicker way of determining the next move that doesn't require you
search through all the nodes in the game tree one by one; if you can
see how to do this, feel free to do things that way instead.
The function generate_game_tree(),
if implemented correctly, returns the same game
tree every time it is invoked. For this reason, and the fact that
generating the game tree is a computationally intensive procedure, you
should only generate the tree once during execution. To this end, the ProfessionalPlayer
class generates the tree when the class is defined and stores the root
of the tree as the static attribute gt_root. You should
make use of this static attribute whenever
accessing the game tree, rather than repeatedly generating a new game
tree.
There are a few important notes, guidelines and
recommendations that should be considered while you design and code the
ProfessionalPlayer class:
generate_game_tree method.
Instead, think about the main steps of the algorithm (e.g.
populating the tree with valid board nodes, and rating each board node)
and code/test these separately.play_turn
method. Write unit tests
for the play_turn method of the ProfessionalPlayer class, and write unit
tests for the generate_game_tree() method. All these unit
tests are to
be placed in the file testprofessional.py.
Testing play_turn for every possible
board configuration in the game tree would be very intensive; instead,
test 3
cases that you
feel are important and, in the comments of your unit test, explain why
you chose these cases.
Testing that the game tree is properly
constructed by generate_game_tree() requires some
creativity. One way is to create and verify
the entire game tree by hand and then ensure that it matches the tree
generated by your code. This is obviously unrealistic. Instead be
creative and think of heuristic ways of testing that the game tree is
constructed properly. For example, what should the 'turn' value of a
node be in each subsequent level of the tree? What should the board
method is_game_over() return for boards associated with
leaf nodes? What should the height of the tree be? And so forth. Again,
you don't need to go overboard, but show that you've put some thought
into verifying that the game tree is constructed correctly.
board.py
amateurplayer.py
tournament.py
testboard.py
testamateur.pynode.py
professionalplayer.py
testprofessionalplayer.py
We have also included a main.py
file with example code for running the Amateur vs. Amateur player
tournament, as well as the Professional vs. Amateur player tournament.
Start
this assignment early, it’ll take a while. Expect the
ProfessionalPlayer coding tasks to consume more than 50% of the
programming time.