Assignment #2 – Recursion and Backtracking
Due June 20, 2008 1pm
Part 1 - Reversing the ordering of a Binary Search Tree (10%)
(Although the necessary details for this problem are given in the
statement below, we will cover Binary Search Trees in more detail in
Lecture 5. You may find reading section 5.6 in the text informative, or
you may be more comfortable postponing working on this problem until
after lecture 5.)
A Binary Search Tree (BST) is a binary tree in which
- each node is labelled
- each node label is
- greater than the labels of all nodes in its left subtree and
- less than the labels of all nodes in its right subtree
For example, consider the following tree:
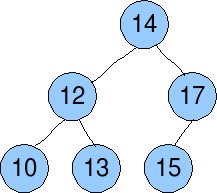
This is a BST because it satisfies the given properties. If you try
doing an inorder traversal of a binary search tree, the order in which
nodes are visited are the ascending order of the node's labels. In the
example tree above, the in order traversal would visit nodes in the
following order:
10,12,13,14,15,17
Your goal is to "reverse" a binary search tree recursively so that each
node label is
- less than the labels of all nodes in its left subtree and
- greater than the labels of all nodes in its right subtree
An inorder traversal of a "reversed" BST will now visit nodes in the
reverse order of the way they were visited in the original tree -- that
is, in descending order of the node labels.
Your recursive procedure must ensure
that if a node is at level k in the original tree, it remains at level
k in the new tree. Hence, you have to be careful about how your
reverse procedure works.
Details
The tree that you'll be reversing will be represented using the "nodes
and references" representation we discussed in class. Download the file
bst.py. It contains a definition of the BSTNode
class. It also contains an empty definition for the function
reverse(root), which takes the root node of the tree to be
reversed as a parameter. You have to fill in the details of this
function. Note that reverse() does not return a new tree. It simply
reverses the tree "in place", so that when the function is done, the
tree pointed at by root contains the reversed tree.
You can download testbst.py which gives you a
couple of examples of how we expect your code to work.
Marking & What to Submit
Correctness 100%
The correctness is based on auto-testing, and proper use of recursion.
(You cannot submit an iterative algorithm.) The only file that you
should submit is bst.py. Do not make
any changes to the definition of the BSTNode class, or the definition
of the reverse() function header. You are free to add code to
the reverse() function, and add any helper functions or any other code
that you feel that you need.
Although you do not need to submit any nose unit tests, you should test
your code carefully to make sure it works.
Part 2 - Grid Generated Mathematical Expressions (90%)
Introduction to Backtracking
In general, a recursive function or method is one that makes a
call to itself. In class, the recursive algorithms that we saw were
generally structured as follows:
-
Check if the subproblem being solved for is small enough to
solve directly (i.e., is it a 'base case'). If it is, return the
solution to the subproblem.
-
Otherwise recursively call the algorithm on a smaller version of
the problem, and then use the solution to the smaller problem to
determine the solution to the original problem.
This approach works well for problems whose solutions can be
expressed in terms of solutions to smaller subproblems. For example,
a recursive algorithm for calculating n! (n factorial) easily follows
from the fact that n! = n*(n-1)! when n>0 and n! = 1 when n=0.
Recursion is also typically used by algorithms that employ backtracking. We introduce the
idea of backtracking and what it's about by way of an example.
Consider the following problem. You are at the entrance to a large
maze that you need to find your way through. Initially, there's
two directions you can travel in the maze: either left or right. If
you choose to go right, then the subproblem you have to solve is how
to find your way out of the maze having gone right in the initial
step; if you choose to go left, then the subproblem you have to solve
is how to find your way out of the maze having gone left in the
initial step. At each junction in the maze you have to choose some
direction to go. After making a choice at each junction, you have a
smaller subproblem to solve: how to get out of the maze
having made the choices you've made thus far. But there's a catch.
What if you made a choice that leads you to a dead end? That is, you
may end up trying to solve a "subproblem" that has no solution. If
you're
lucky, this won't happen and each choice you make will get you closer
to the maze's exit. If you're unlucky, then you'll have to return to
a junction point that you previously visited and make a different
choice for which direction to go. In other words, you will have to
backtrack.
How can
recursion be used to do this backtracking? Lets define a function mazeSolve(path)
that returns True or False whether there exists a way out of the maze
using the sequence of choices that's been made thus far (stored in path).
It will be invoked as follows
path = []
is_solvable = mazeSolve(path)
If there is a way out of the maze, then is_solvable will be assigned
True, and the sequence of choices required will be contained in path.
We now provide a very high-level
implementation of the mazeSolve function.
def mazeSolve(path):
- if the current sequence of choices in path leads to a
dead end:
return False
- if the current sequence of choices leads
to the maze exit (without any more junctions):
return True
- # (if we reached this point, it means we have to make a choice of
direction at another junction)
- for each choice of direction at the current junction:
- add the choice to the path
- invoke mazeSolve recursively, with the updated path variable
(that is, call
mazeSolve(path) )
- if the return value is True, then a path out of the maze has
been found and we immediately
return True to the caller
- if the return value is False, then the choice we just made
resulted in a dead end and we have to try the other choices
- if every possible choice of direction at the current junction
leads to a dead end, we have to backtrack to the previous junction and
make a different choice there. This is done by returning False.
There are a lot of details omitted from the above description, but it
should give you an idea of how recursion can be used to do
backtracking. In particular, each recursive call to mazeSolve advances
to the next junction in the maze, and whenever a call to mazeSolve
returns, it backtracks to an earlier position in the maze.
In the context of the maze
problem and the description we gave above, the term 'backtracking'
has a taken on a very specific meaning: you are physically backtracking
to a
previous position in the maze because an earlier choice you made led
you to a dead end. More generally, backtracking is a technique
for systematically exploring the set
of all possible solutions to a problem.
In the maze problem, for
example, the set of all possible solutions is the set of all
sequences of choices that can be made at junctions. mazeSolve
explores this set systematically until it hits upon a correct
solution. Even though mazeSolve stops after finding one correct
solution, there may be other ways through the maze. One can modify the
technique given in mazeSolve to find all
possible ways through the maze. Think about how you might do this and
what changes you would need to make. You will need to do something
similar in one part of the problem explained below.
The Problem – Grid Generated Expressions
With that introduction out of the way, we are now ready to
describe the main problem that you'll be working on in this
assignment.
You are given an n x n grid of integers. For example, consider the
following grid (where n = 3):
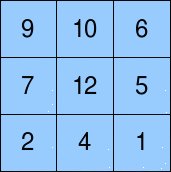
Pick a starting position in the grid.
From this position in the grid, you can move to any adjacent square.
That is, you can move up, down, left, right, diagonally up and left,
diagonally up and right, diagonally down and left, and diagonally
down and right (assuming, of course, this doesn't move you off the
grid). The grid does not "wrap around".
(For example moving left when there's no grid position to the left does
not put you in a cell at the
rightmost side of the grid.)
After moving to some square, you can keep moving to adjacent
squares as long as you don't revisit a square at which you were
previously. You can stop moving at any point you wish (there is
no
requirement that you vist every grid position). In this manner, a path
through the grid can be traced
out.
Based on the path that you traced out, a mathematical expression
involving only + and - is written by making the sequence of operands in
the expression the same as the sequence of
numbers in the grid positions visited, and by choosing + or - as the
operator between each operand. An expression that can be created in
this manner with a grid G is said to be a G-generated expression.
For example, “9+10+6” is a G-generated expression (where G is the
grid above). To see why, trace the path that starts at position
(0,0) , moving right until the last column in
reached. The sequence of numbers in the visited grid positions is
(9,10,6). We use this sequence of numbers as the sequence of operands
in our expression, and place the + operator between each operand. The
expression “2+6+1” is not G-generated since there is no way of visiting
the sequence of grid positions containing 2,6,and 1. Other examples of
G-generated expressions: "12-10+7", "6-5-1", "7-9". Other examples of
expressions that are not G-generated: "20+10", "4-4-4-2".
There are two problems you have two solve:
Problem 1
Given a grid G, and a mathematical expression (as a string), you
have
to determine if the string is G-generated. You can always assume
the expression given will be well-formed and will only contain
operators + or -.
Problem 2
Given a grid G, an integer result, and
an integer
stipulating the number of operands numterms, find all
expressions containing numterms operands that evaluate to
result
and that are G-generated. For example, given the grid G
above,
result = 9, and numterms = 2, the possible
expressions are “4+5”,
“5+4”, “7+2” and “2+7”.
Details
Download the starter code here: numbergrid.py,
testnumbergrid.py.
numbergrid.py defines a class NumberGrid whose constructor takes 1
parameter: a 2D list (list of lists) representing the square grid G. A
position in the grid is a 2 element tuple. More precisely, the first
element of the tuple indexes
a 1D list, and the second element indexes an element in the list
indexed by the first tuple. (The first element is the "row" in the
grid, and the second element is the "column".)
There are two methods you have to implement
def is_expr_valid(self, expr):
''' returns true or false based on whether the given
expression is G-generated '''
def find_all_exprs(self, result, numterms):
''' returns a list of all possible
expression strings that
evaluate to the given result, contain exactly numterms operands,
and are G-generated.'''
Do not modify the header definitions
for these functions, or the constructor for NumberGrid. Note:
expression strings passed in as arguments to is_expr_valid will never
contain any spaces, and the expressions in the list returned by find_all_exprs
should not include any spaces either.
Hints and Tips
- Be efficient with your recursion and backtracking. When we grade
your submitted program, we will be running a number of test cases, each
of which will be given a limited amount of time to run. If it exceeds
this time, the test case will be flagged as a failure. As rough
guidelines,
find_all_exprs shouldn't take longer than the
max time in the following chart:
Grid Size
|
Number of operands in expression
(numterms)
|
Max time taken by find_all_exprs
|
3x3
|
8
|
25 seconds
|
3x3
|
7
|
15 seconds
|
3x3
|
6
|
5 seconds
|
3x3
|
5
|
2 seconds
|
3x3
|
<5
|
< 1 second
|
4x4
|
6
|
40 seconds
|
4x4
|
5
|
6 seconds
|
4x4
|
< 5
|
< 1 second
|
- The reason for the dramatically increasing times with only a
slight increase in the size of the problem has to do with the
combinatorial explosion of the number of paths in the grid.
- The above are only rough guidelines. When using smaller grids and
searching for expressions with fewer operands, the time taken should be
less. Also,
is_expr_valid should be a lot faster than find_all_exprs
(for an expression with 8 operands in a 4x4 grid, it should only take a
fraction of a second).
- The choice for grid size and number of operands in the above
chart is not meant to imply that we will limit our testing to grids of
those size. We may test other cases as well (smaller or bigger).
- In order to make your program as efficient as possible:
- For
is_expr_valid, if you determine that a
particular expression is not G-generated before you've examined the
whole string, return that result to the caller as soon as you can.
Don't keep doing needless work.
- For
find_all_exprs, if you are asked to only find
expressions with numterms operands, do not waste time on
expressions longer than numterms operands. As part of finding
expressions with numterms operands, you may have to do some processing
on expressions that have fewer than numterms operands, but that cannot
be avoided.
What to Submit
You have to submit numbergrid.py (and any other helper
modules you
create).
You have to test your code using nose, but you do not
have to submit your nose test cases. Instead, you have to submit a
testing document named test.txt that describes the test
cases that you ran, why you
felt each test was necessary, and why your set of test
cases is sufficient for ensuring the likelihood of bugs in your program
is minimal. This document must be
written in plain text, and must be readable with a unix-based text
editor (such as vi or pico). The testing document will be
graded on both content and style (i.e., make sure you use correct
spelling and grammar).
Marking
Correctness 50%
Commenting/Code Style/Design 25%
Testing document 25%

