Abstract: Meshes representing real world objects, both artist-created and scanned, contain a high level of redundancy due to (possibly approximate) planar reflection symmetries, either global or localized to different subregions. An algorithm is presented for detecting such symmetries and segmenting the mesh into the symmetric and remaining regions. The method, inspired by techniques in Computer Vision, has foundations in robust statistics and is resilient to structured outliers which are present in the form of the non symmetric regions of the data. Also introduced is an application of the method: the folding tree data structure. The structure encodes the non redundant regions of the original mesh as well as the reflection planes and is created by the recursive application of the detection method. This structure can then be unfolded to recover the original shape. Applications include mesh compression, repair, skeletal extraction of objects of known symmetry as well as mesh processing acceleration by limiting computation to non redundant regions and propagation of results.
Key words: symmetry, planar symmetry, reflective symmetry, symmetry detection, local symmetry detection, partial symmetry detection, approximate symmetry detection, mesh segmentation, symmetry segmentation, symmetry-based segmentation, hierarchical segmentation.
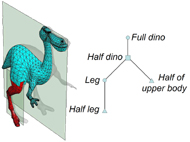
Overview: Our approach to finding maximally symmetric parts is based on robust M-estimation using an iteratively reweighted least squares (IRLS) algorithm. We simultaneously solve for the reflection plane as well as the region of surface that is symmetric with respect to it. Upon convergence, the symmetric region found is separated from the rest. The algorithm is then applied to the remaining regions to find other local symmetries, as well as recursively to half of the symmetric region to find nested symmetries. This process leads to a hierarchical folding tree representation of the object where geometry is only stored in tree leaves. The original surface can then be reconstructed from its folding tree in a bottom up fashion by reflecting symmetric geometry and reconnecting segmentation boundaries.
Errata:
-
In section 6. Conclusions and future work where it reads "We have proposed a novel approach for finding global planar symmetries in 3D meshes [...]" it should read "We have proposed a novel approach for finding global as well as local planar symmetries in 3D meshes [...]"