Welcome to the Compression Trinity Hub
Large Language Models (LLMs) have become foundational tools in modern artificial intelligence, but their remarkable capabilities come at a significant cost. Training and deploying these models consumes enormous computational and memory resources.
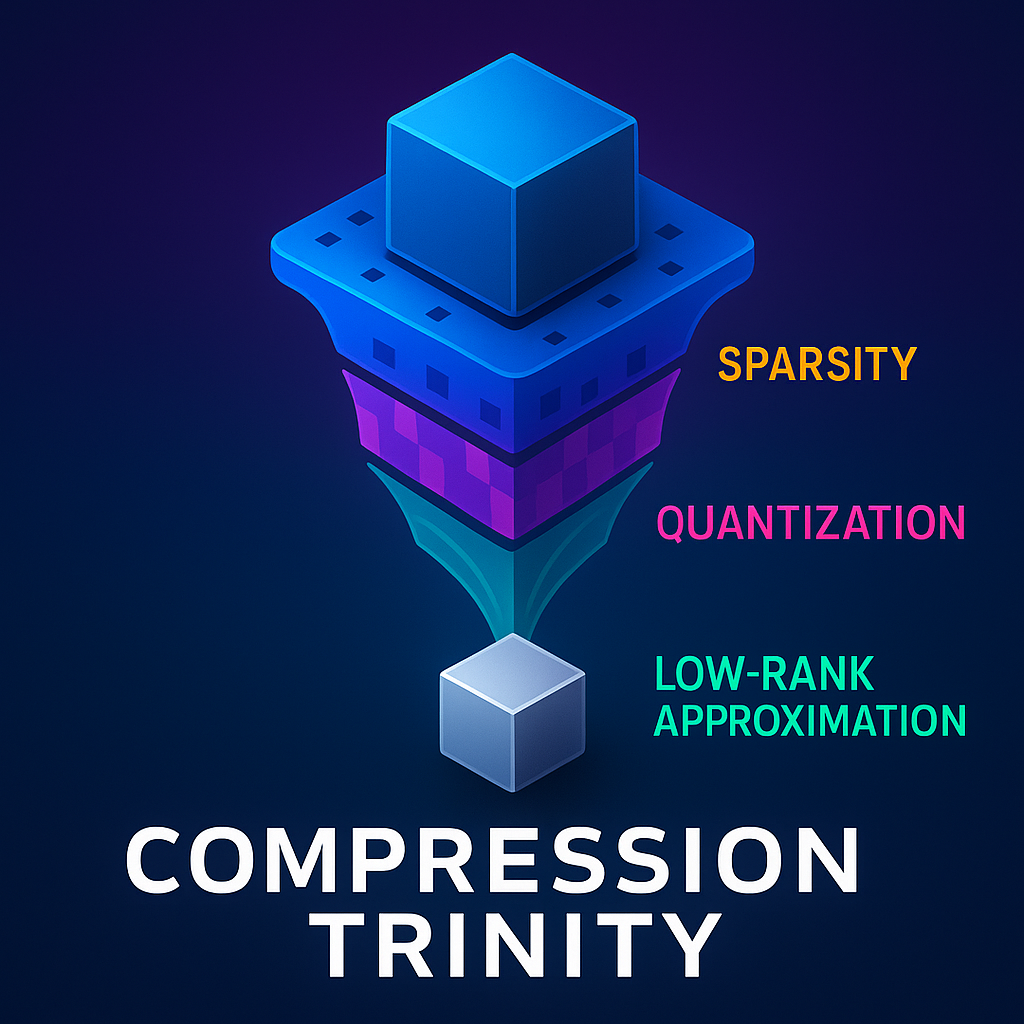
To mitigate these overheads, various compression techniques have been proposed, primarily sparsity (removing parameters), quantization (reducing parameter precision), and low-rank approximations (factoring parameter matrices). Historically, these methods have often been applied in isolation, an approach that is inherently limiting.
This hub is built around a conceptual framework, the Compression Trinity, which argues for the joint application of these three pillars. These methods are highly complementary, as they primarily target distinct bottlenecks of modern hardware:
- Sparsity is chiefly aimed at reducing the computational load.
- Quantization is aimed at reducing memory bandwidth requirements.
- Low-rank approximations are aimed at exploiting and compressing parameter redundancy.
Through my research, I've developed novel approaches that integrate these techniques to push the boundaries of what's possible in model compression. Here, you'll find insights from my papers, MKOR, SLoPe, SLiM, PATCH, and OPTIMA, each contributing unique advancements to the field. Join me in exploring how these methods are shaping the future of efficient AI.
Pillar 1: Sparsity
Sparsity is a compression technique that involves identifying and removing (i.e., setting to zero) the least important weights in a neural network, thereby reducing the total number of parameters and floating-point operations (FLOPs).
This technique is broadly categorized into two types. Unstructured sparsity removes arbitrary, individual weights from a matrix. While it offers high flexibility, it is notoriously difficult to accelerate on modern parallel accelerators like GPUs due to its irregular memory access patterns. Conversely, structured sparsity removes entire blocks of parameters, such as full rows or columns. This regular structure is hardware-friendly but often damages model accuracy significantly.
A new family of semi-structured sparsity patterns has emerged to bridge this gap. A prominent example is N:M sparsity, which enforces that $N$ out of every $M$ consecutive weights are non-zero (e.g., 2:4 sparsity). This pattern is flexible enough to preserve accuracy while being regular enough for hardware acceleration on modern GPUs.
Pillar 2: Quantization
Quantization reduces the numerical precision of the numbers used to represent the model's weights and, in some cases, activations. For example, parameters are typically trained in 32-bit (FP32) or 16-bit (FP16/BF16) floating-point formats, but quantization can compress them down to 8-bit integers (INT8), 4-bit integers (INT4), or even lower bit-widths.
This reduction in precision has two primary benefits: it saves memory (e.g., 4-bit quantization yields an 8x memory reduction over 32-bit weights) and allows for the use of faster, specialized compute units (like INT8 tensor cores) that can perform integer arithmetic much faster than floating-point operations.
The main challenge is that the representation capabilities of the numbers are reduced exponentially with the bit-width. This can lead to large accuracy degradation, especially in the presence of outlier values, which are common in LLMs.
Pillar 3: Low-Rank Approximation
Low-rank approximations are based on the observation that the large weight matrices in LLMs are often over-parameterized and have a low "intrinsic rank." This redundancy can be exploited by decomposing a large weight matrix (e.g., $W$) into the product of two smaller, "thin" matrices (e.g., $L$ and $R$), where the inner dimension (or "rank") $r$ is much smaller than the original dimensions.
This technique, popularized by Low-Rank Adaptation (LoRA), can significantly reduce the memory and compute overhead of LLMs. However, low-rank approximations are not very effective in compressing matrices that are inherently high-rank, and applying them too aggressively can lead to significant errors.
Applying the Trinity Across the LLM Life-cycle
The principles of the Compression Trinity are not applied uniformly; they are adapted to the unique challenges of each stage of an LLM's life-cycle. My research provides a suite of tools that target these distinct phases:
1. Accelerating Pretraining
In the computationally expensive pretraining phase, SLoPe lays the foundation for the Trinity. It introduces a framework that jointly applies sparsity and low-rank approximations from the start. It uses a novel double-pruned backward pass for acceleration and inserts "lazy" low-rank adapters in the final iterations to recover accuracy. This creates an efficient base model that is ideal for subsequent quantization.
2. Efficient Post-Training Compression for Inference
For the inference stage, the goal is to compress a pre-trained model in one shot with minimal accuracy loss. This is where the challenge of compounded error, where errors from sparsity and quantization add up, is most severe.
- SLiM provides the complete, one-shot solution by holistically integrating all three pillars. It mathematically computes the optimal low-rank adapters to compensate for the joint error from hardware-friendly sparsity and quantization.
- OPTIMA perfects the sparsity pillar by using quadratic programming to find the optimal post-pruning weight update. This creates a highly accurate and stable sparse model that can withstand subsequent quantization.
- PATCH also strengthens the sparsity pillar by introducing a learnable, hybrid sparsity pattern that mixes dense and 2:4 sparse tiles, balancing accuracy and hardware speedup.
- BEAM proposes a cheap alternative to fine-tuning of LLMs post compression to recover the lost accuracy without adding significant computational overhead.
3. Beyond Model Weights: Optimizing the Optimizer
My research also demonstrates the general-purpose power of these principles by applying them to the optimization process itself. MKOR is a novel second-order optimizer that leverages all three pillars, using sparsity to approximate second-order info, low-rank updates to compute its inverse, and quantization for a stable 16-bit implementation, to accelerate the training process from a different angle.
Stay Updated with the Latest Findings
The field of model compression is rapidly evolving, with new techniques and optimizations emerging regularly. To keep you informed about the latest advancements and insights from my research, I regularly publish blog posts on this website. These posts delve into recent findings, experimental results, and practical tips for applying compression techniques to your own models. Check out the latest posts on the side bar on this page!
Acknowledgements
I would like to express my sincere gratitude to Dr. Amir Yazdanbakhsh and Prof. Maryam Mehri Dehnavi for their constant support and invaluable feedback on my research. Their guidance and insights have been instrumental in shaping and advancing this work in LLM compression.